Il percorso più rapido¶

Risolviamo un ultimo problema, affrontando ancora una volta questioni geometriche e infinitesimali, che ci permetteranno di giustificare un’altra legge della fisica.

Da A a B nel tempo più breve¶

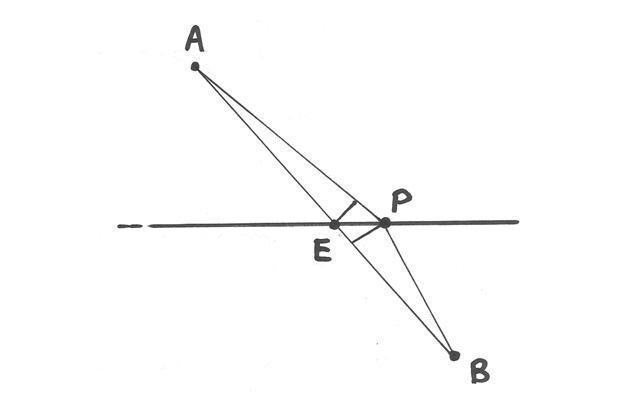
Questa volta la retta orizzontale deve essere attraversata per poter raggiungere B partendo da A. La complicazione è che, oltrepassando la retta, si è costretti a una velocità diversa. In pratica:

Bisogna trovare il percorso che minimizzi il tempo nell’andare da A a B.

Il problema (la retta orizzontale rappresenta la separazione fra mezzi diversi).

Nel problema del capitolo precedente non c’era la complicazione della velocità: tutto si svolgeva istantaneamente. Quando la velocità è costante, il percorso di tempo minimo è senz’altro il tratto più breve: un segmento AB che attraversa la retta in un punto E, all’intersezione fra il segmento e la retta.

Nelle nuove condizioni, però, il segmento AB non è sicuramente la soluzione ottimale. Infatti è conveniente che la parte più breve del percorso si trovi nel semipiano più lento, anche a costo di spezzare il segmento in due tratti disuguali. Occorre cercare P, il punto “di equilibrio” sulla retta, che pur allungando i due tratti della spezzata, lo fa in modo che il tempo perso a percorrere la parte più lenta si recuperi al meglio nella parte più veloce. Abbiamo la possibilità di costruire la soluzione esatta ricorrendo all’analisi.

Risolvo con gli iperreali e la geometria¶

Immaginiamo che nella parte superiore del disegno la velocità sia 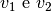$v_1 \ \mbox{e}\ v_2$ sia nella parte inferiore e sia 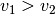$v_1 > v_2$ ; per il resto seguiamo i ragionamenti del problema precedente.

Un punto X sulla retta, diverso da P, darà luogo a un tempo di percorrenza diverso. Continuando a “muovere” X sulla retta i tempi totali cambiano, trovano il valore minimo e poi aumentano. Il grafico che ne deriva è simile a quello del problema precedente.

Fermiamoci dove immaginiamo che X rappresenti la posizione cercata. Allora un punto X’ infinitamente vicino darà luogo ad un tempo diverso da quello calcolato per X, ma solo per infinitesimi di ordine superiore e quindi un tempo indistinguibile.

La soluzione, studiando la geometria del problema e con l’aiuto dell’analisi matematica.

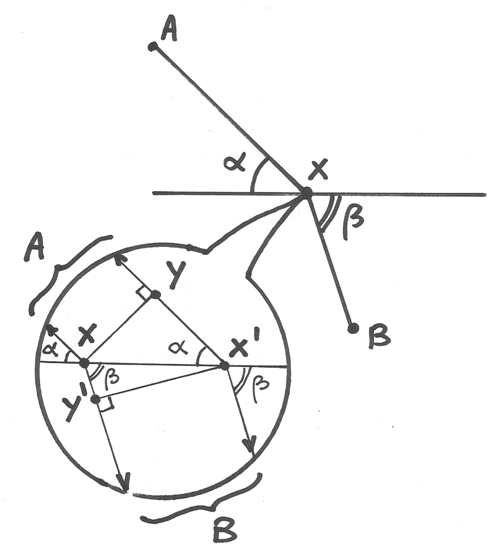
Puntiamo su X il microscopio non standard e ingrandiamo fino a vedere distinti X e X’. Se i tempi dei due percorsi sono indistinguibili, allora i segmenti su X e X’ provenienti da A e da B saranno indistinguibilmente paralleli. AX e AY sono tratti uguali, percorsi nello stesso tempo, mentre X’Y è il segmento che causa ritardo nel percorrere AX’, rispetto a AX. Si tratta di un ritardo infinitesimo, calcolabile in 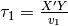$\tau_1=\frac{X'Y}{v_1}$ . 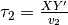Perché i due percorsi AB avvengano indistinguibilmente nello stesso tempo, occorre che tale ritardo sia compensato, andando verso B, dal ritardo $\tau_2 =\frac{XY' }{v_2}$ dovuto al tratto XY’ sul segmento XB, più lungo rispetto a X’B. Ricaviamo quindi

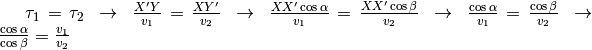$\tau_1=\tau_2\ \rightarrow\ \frac{X'Y}{v_1}=\frac{XY'}{v_2}\ \rightarrow\ \frac{XX'\cos \alpha}{v_1}=\frac{XX'\cos \beta}{v_2}\ \rightarrow\ \frac{\cos \alpha}{v_1}=\frac{\cos \beta}{v_2}\ \rightarrow\ \frac{\cos \alpha}{\cos \beta}=\frac{v_1}{v_2}$ .

Il rapporto fra gli angoli fissa univocamente l’inclinazione dei segmenti rispetto alla retta e di conseguenza fissa il punto ottimale X. Quindi la soluzione è: Il percorso più rapido è una spezzata fatta da due segmenti AX e XB. I coseni degli angoli in X, fra i due segmenti e la retta, sono direttamente proporzionali alle velocità di percorrenza dei due tratti.

La rifrazione della luce¶

Si può riscrivere la soluzione considerando gli angoli 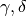$\gamma, \delta$ complementari di 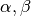$\alpha, \beta$ , cioé considerando gli angoli che i due segmenti formano con la normale alla retta nel punto X . Allora la relazione diventa:

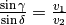
$\frac{\sin \gamma}{\sin \delta}=\frac{v_1}{v_2}$

Se pensiamo alla situazione fisica di un raggio luminoso che attraversa la superficie di separazione (la retta) passando per due mezzi con diversa densità, la legge individuata è la legge di Snell per la rifrazione e l’ultimo rapporto è detto indice di rifrazione fra due mezzi. Concludiamo quindi che il raggio luminoso in questa situazione non percorre il cammino più breve, ma quello più rapido.