Distanze sulla retta iperreale¶
La retta e i numeri iperreali¶
Abbiamo usato un modello di retta che, grazie a strumenti non standard, permette di visualizzare anche i numeri non standard. I punti della retta iperreale sono in corrispondenza biunivoca con i numeri iperreali. Gli iperreali (insieme *R) sono: i numeri standard, cioè i numeri reali (insieme R), e i numeri non standard. I numeri non standard sono: gli infiniti, gli infinitesimi e una parte dei finiti non infinitesimi.
Sappiamo già che sulla retta reale ogni punto corrisponde ad un numero reale e che fra due punti, per quanto vicini, saremo sempre in grado di collocarne un terzo. La distanza di questo terzo punto dagli altri due sarà molto piccola, ma finita. Non infinitesima. Sappiamo anche che i punti sono infiniti, cioè che possiamo sempre collocare un punto più a destra o più a sinistra degli altri. Ma per quanto sia infinito l’insieme dei numeri reali, tuttavia i numeri reali infiniti non esistono. Sulla retta iperreale le cose sono diverse.
Non ci sono dimostrazioni che confermino la corrispondenza biunivoca fra i punti della retta (reale o iperreale) e i numeri corrispondenti. La assumiamo per vera, cioè come postulato implicito nella scelta del modello di retta. Se non fosse così, cioè se la retta “avesse dei buchi” o se mancassero dei numeri per esprimere la posizione di alcuni punti, la retta (reale o iperreale) sarebbe un modello inutile.
Distanze infinitesime, monadi e numeri finiti¶
Esistono gli infinitesimi e quindi esistono le distanze infinitesime. Un numero
x è infinitamente vicino ad un numero y (si scrive 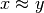 ) se
) se
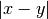 è un infinitesimo.
L’insieme dei numeri iperreali a distanza infinitesima da x si chiama monade di
x: mon(x). mon(x) è in pratica il campo visivo di un microscopio non
standard puntato su x.
Fra le monadi, la principale è mon(0), infatti lo zero è “circondato” da
infinitesimi. Se x è un infinitesimo, potremo scrivere
è un infinitesimo.
L’insieme dei numeri iperreali a distanza infinitesima da x si chiama monade di
x: mon(x). mon(x) è in pratica il campo visivo di un microscopio non
standard puntato su x.
Fra le monadi, la principale è mon(0), infatti lo zero è “circondato” da
infinitesimi. Se x è un infinitesimo, potremo scrivere 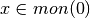 o
più semplicemente
o
più semplicemente 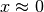 .
La distanza fra due numeri standard è zero oppure è finita. Quindi fra due
numeri standard a, b non può succedere che
.
La distanza fra due numeri standard è zero oppure è finita. Quindi fra due
numeri standard a, b non può succedere che 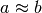 , a meno che
non coincidano. Così due numeri standard non possono appartenere alla stessa
monade.
È facile vedere che l’essere infinitamente vicino è una relazione di
equivalenza. Per questo individua una partizione sulla retta iperreale.
Le monadi ricoprono la retta senza sovrapporsi, “centrate” ognuna su un numero
finito diverso. Le monadi dei numeri finiti contengono un numero standard, uno
al massimo.
Anche i numeri infiniti hanno proprie monadi e possono essere infinitamente
vicini.
Ogni numero finito x si può esprimere come
, a meno che
non coincidano. Così due numeri standard non possono appartenere alla stessa
monade.
È facile vedere che l’essere infinitamente vicino è una relazione di
equivalenza. Per questo individua una partizione sulla retta iperreale.
Le monadi ricoprono la retta senza sovrapporsi, “centrate” ognuna su un numero
finito diverso. Le monadi dei numeri finiti contengono un numero standard, uno
al massimo.
Anche i numeri infiniti hanno proprie monadi e possono essere infinitamente
vicini.
Ogni numero finito x si può esprimere come 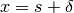 , con s che
è la sua parte standard (s=st(x)) e mentre
, con s che
è la sua parte standard (s=st(x)) e mentre 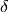 è la sua parte
infinitesima (eventualmente nulla).
Se la parte infinitesima di un numero finito è nulla, il numero coincide con la
sua parte standard.
Invece, se è nulla la sua parte standard, il numero finito è un infinitesimo.
Le parti standard dei numeri finiti si sommano come avviene per i numeri reali:
sicché la somma della parti standard è la parte standard della somma.
Anche le parti infinitesime di due numeri finiti sono sommabili e sappiamo,
dalla tavola della somma, che la loro somma è un infinitesimo.
è la sua parte
infinitesima (eventualmente nulla).
Se la parte infinitesima di un numero finito è nulla, il numero coincide con la
sua parte standard.
Invece, se è nulla la sua parte standard, il numero finito è un infinitesimo.
Le parti standard dei numeri finiti si sommano come avviene per i numeri reali:
sicché la somma della parti standard è la parte standard della somma.
Anche le parti infinitesime di due numeri finiti sono sommabili e sappiamo,
dalla tavola della somma, che la loro somma è un infinitesimo.
Distanze finite e galassie¶
Due numeri a distanza finita si dicono finitamente vicini.
Quindi, in questo caso 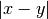 è un numero finito. Come per la distanza
infinitesima, anche la distanza finita è una relazione di equivalenza,
che quindi individua una partizione nell’insieme *R.
Tutti i numeri a distanza finita da un certo numero x costituiscono la
sua Galassia:
è un numero finito. Come per la distanza
infinitesima, anche la distanza finita è una relazione di equivalenza,
che quindi individua una partizione nell’insieme *R.
Tutti i numeri a distanza finita da un certo numero x costituiscono la
sua Galassia:
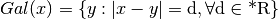 .
x è un qualsiasi iperreale.
.
x è un qualsiasi iperreale.
Se x = 0, gli y a distanza finita da x
determinano l’insieme dei numeri finiti. Gal(0) per questo motivo è detta
galassia principale. Occorre ricordare che l’espressione “a distanza finita”
non vuol dire che la distanza sia un numero standard, ma che è un numero
finito, quindi esprimibile come 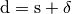 .
La parte infinitesima può essere eventualmente nulla, ma non è detto che lo sia.
Per questo la galassia principale contiene tutti i numeri finiti, standard e
non standard.
I numeri a distanza finita da x si visualizzano mettendo in
corrispondenza di x un telescopio standard e puntandolo verso
gli altri numeri della galassia.
.
La parte infinitesima può essere eventualmente nulla, ma non è detto che lo sia.
Per questo la galassia principale contiene tutti i numeri finiti, standard e
non standard.
I numeri a distanza finita da x si visualizzano mettendo in
corrispondenza di x un telescopio standard e puntandolo verso
gli altri numeri della galassia.
Se x è un numero infinito, Gal(x) è l’insieme dei numeri a distanza finita da x, che sono tutti infiniti (vedi per questo la tavola della somma). Poiché i numeri infiniti sono ..infiniti, sono infinite anche le loro galassie. La retta iperreale contiene quindi infinite galassie, oltre alla galassia principale.
Distanze tali da rendere i numeri indistinguibili¶
Due numeri non nulli si dicono indistinguibili se la loro differenza
è infinitesima rispetto a ciascuno di essi. Cioé:
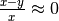 e
e 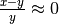 .
x indistinguibile da y si scrive:
.
x indistinguibile da y si scrive: 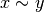 .
.
Immaginiamo di collocare due numeri non nulli sulla retta iperreale.
Se sono infinitesimi e non si riesce a cogliere la loro distanza nel campo
visivo del microscopio non standard che visualizza uno dei due,
allora sono indistinguibili.
Se invece sono infiniti, sono indistinguibili se lo zoom non standard, che
visualizza uno dei due, non riesce a separarlo dall’altro.
In pratica sono indistinguibili se non si riesce a cogliere la loro differenza
nella stessa scala (di riduzione o di ingrandimento) con cui si visualizzano.
È importante che i numeri (e i segmenti corrispondenti) non siano nulli, perché
a qualsiasi scala il punto ha lunghezza uguale a zero e quindi il rapporto
della definizione non avrebbe senso.
Tornando alla definizione, da 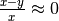 risulta
risulta
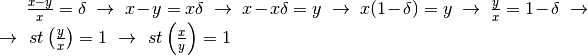 .
.
Quindi una definizione equivalente di indistinguibili è: Due numeri si dicono indistinguibili se la parte standard del loro rapporto vale 1. Oppure, che è lo stesso: ... se il loro rapporto è infinitamente vicino a 1. Ovviamente se due numeri sono indistinguibili, sono dello stesso tipo.
Alcuni dettagli sugli indistinguibili in relazione ai loro tipi.
(Ricorda che a rappresenta un numero di
tipo fni, 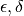 rappresentano inn, M rappresenta
un numero di tipo I, mentre x,y sono di tipo qualsiasi).
rappresentano inn, M rappresenta
un numero di tipo I, mentre x,y sono di tipo qualsiasi).
- Aggiungere un infinitesimo ad un numero non infinitesimo produce un risultato
indistinguibile:
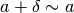 .
. - Per due numeri di tipo fni essere indistinguibili o essere infinitamente
vicini è la stessa cosa:
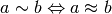 .
. - Due infinitesimi sono sempre infinitamente vicini, ma non è detto che siano
indistinguibili. Per essere indistinguibili devono differire per un
infinitesimo di ordine superiore:
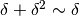 .
. - Quindi:
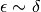 e
e 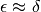 sono
relazioni
diverse perché la seconda è sempre vera, mentre la prima può non esserlo.
Per esempio due infinitesimi dello stesso ordine come
sono
relazioni
diverse perché la seconda è sempre vera, mentre la prima può non esserlo.
Per esempio due infinitesimi dello stesso ordine come
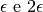 sono distinguibili perché la parte standard del loro rapporto è diversa da 1.
sono distinguibili perché la parte standard del loro rapporto è diversa da 1. - Per gli infinitesimi, l’essere indistinguibili è una condizione più impegnativa che essere dello stesso ordine.
- Due infiniti sono indistinguibili se differiscono di un numero finito oppure
di un numero infinitesimo:
 .
. - Due infiniti sono indistinguibili se differiscono di un infinito di ordine
inferiore:
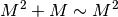 .
. - Per gli infiniti, l’essere indistinguibili è una richiesta meno impegnativa dell’essere infinitamente o finitamente vicini.
Riassumendo¶
Postulato: i punti della retta iperreale sono in corrispondenza biunivoca con i numeri iperreali (insieme *R). Due punti sulla retta iperreale (e i due numeri corrispondenti) possono essere infinitamente vicini o finitamente vicini. Sono due diverse relazioni di equivalenza, che ripartiscono la retta iperreale con monadi o galassie. Inoltre due punti possono essere indistinguibili, cioè così vicini che la loro distanza rapportata a ciascuno dei due è un infinitesimo.
Esercizi¶
- Dimostra che
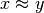 è una relazione di equivalenza
è una relazione di equivalenza - Traduci in formule i due paragrafi sulla somma di due numeri finiti.
- Dimostra le proprietà seguenti:
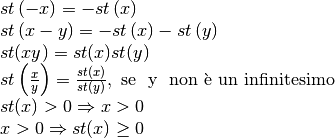
- Sotto quale ulteriore condizione è vera la quarta relazione precedente?
- La catena di deduzioni che viene dalla definizione di indistinguibili, può essere percorsa a ritroso? E vale anche scambiando al denominatore x con y?
- Dimostra a partire dalla definizione che se due numeri sono indistinguibili allora il loro rapporto è infinitamente vicino a 1.
- Gli indistinguibili sono necessariamente dello stesso tipo: vale anche il viceversa?
- Una sola delle seguenti proposizioni è vera: quale? 1) Due infiniti sono indistinguibili se appartengono alla stessa monade o galassia. 2) Due infiniti appartengono alla stessa monade o galassia se sono indistinguibili
- Due infiniti indistinguibili sono necessariamente dello stesso ordine? E due infiniti dello stesso ordine sono necessariamente indistinguibili?
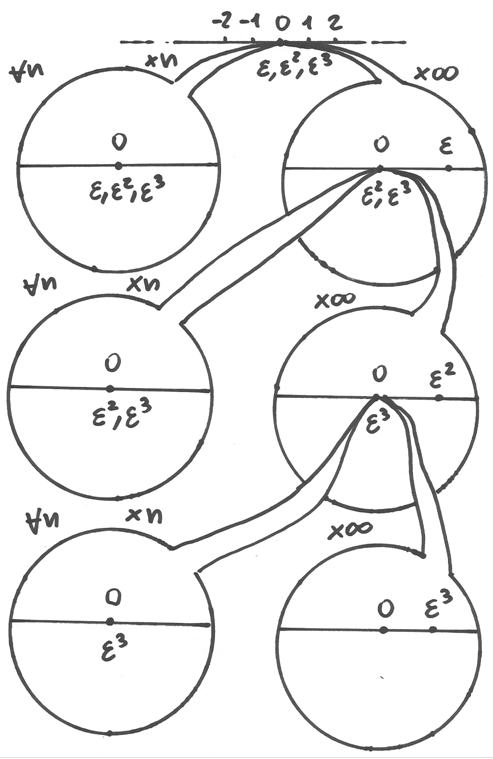
- Quale confronto viene rappresentato dall’immagine che segue? Descrivi il procedimento per risolverlo.