La scatola più capiente¶

Per apprezzare l’efficacia del calcolo con gli iperreali consideriamo alcuni esempi. Sono problemi di ottimizzazione noti, che si risolvono individuando una funzione opportuna e, grazie a questa, calcolando la soluzione utile. Perverremo a una soluzione esatta, usando microscopi telescopi e zoom.

La scatola ottimale¶

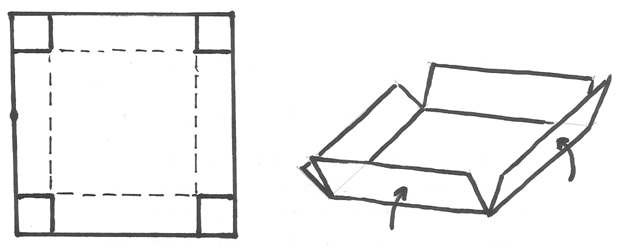
Abbiamo un cartone quadrato di lato un metro e vogliamo costruire una scatola senza coperchio tagliando quattro quadrati uguali nei vertici del cartone e poi sollevando i 4 rettangoli rimasti intorno alla base quadrata. Il problema è: ricavare la scatola che racchiude il volume massimo.

Trova la scatola di volume massimo

È immediato osservare che se il lato dei quadrati è molto piccolo, la scatola avrà un’area di base di poco meno di un metro quadrato, ma un’altezza molto piccola e quindi un volume piccolo. Ancora, se il lato dei quadrati è vicino al mezzo metro, la scatola verrà alta quasi mezzo metro, ma l’area di base sarà piccolissima e il volume sarà pure piccolissimo. È sensato dire che la misura del taglio, cioè il lato di un quadratino, sarà un numero fra zero e mezzo metro. Ma quale numero precisamente?

Se il problema fosse impossibile, ci si potrebbe avvicinare alla soluzione per via numerica, cioè per tentativi. Si immaginano varie misure del taglio, si calcolano di conseguenza i volumi, si confrontano i risultati, si sceglie il più utile. A mano sarebbe lungo e noioso, ma con un programma al computer non sarebbe né lungo né difficile e si approssimerebbe il risultato con precisione senza dubbio sufficiente.

Risolvo con gli iperreali e l’analisi¶

Tuttavia abbiamo la possibilità di ottenere la soluzione esatta con semplici considerazioni geometriche e un po’ di analisi matematica. Poniamo che sia x il lato del quadrato da ritagliare. Il volume si calcola allora con 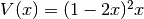$V(x)={(1-2x)^2}x$ (area di base per altezza). I valori di x

Grafico della funzione V(x), volume della scatola: $V(x)={(1-2x)^2}x$ .

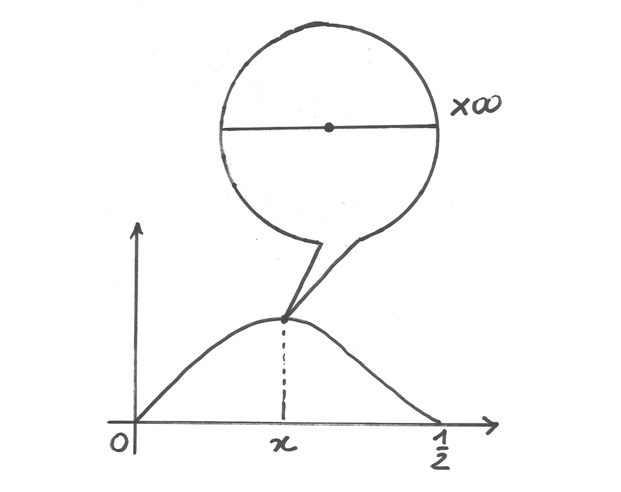
prossimi a zero o a mezzo metro, daranno luogo a volumi praticamente nulli. Altre misure del taglio x produrranno invece volumi crescenti, fino a un massimo, oltre il quale i risultati diminuiscono. Il grafico approssimativo della funzione rappresenta questi ragionamenti. In linea puramente ipotetica i massimi potrebbero anche essere più di uno.

x è il numero che risolve il problema. In corrispondenza di x c’è il punto di massimo. Per numeri prossimi a x (cioè che appartengono alla sua monade) i volumi saranno lievemente inferiori. I tratti infinitesimi che compongono il grafico nelle diverse posizioni saranno variamente inclinati. Ma se osserviamo il punto di massimo con un microscopio non standard vediamo che lì il grafico è indistinguibile da un tratto orizzontale. Ricordiamo che essere indistinguibili ha per conseguenza che nella scala in cui un segmento è visualizzato, un altro ipoteticamente diverso non può apparire distinto, perché differisce per infinitesimi di ordine superiore. Quindi se ci spostiamo nella monade di x, per esempio a destra, in 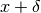$x+\delta$ , anche lì visualizziamo un segmento orizzontale. Come verificare questo attraverso il calcolo?

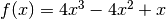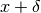Data la funzione del volume $f(x)=4x^3-4x^2+x$ , ne calcoliamo i valori in x e in $x+\delta$ e quindi calcoliamo la loro variazione. Poi useremo gli indistinguibili:

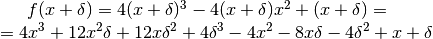
$f(x+\delta)=4(x+\delta)^3-4(x+\delta)x^2 +(x+\delta)=\newline = 4x^3+12x^2\delta+12x\delta^2+4\delta^3-4x^2-8x\delta-4\delta^2+x+\delta$

La variazione di risultato dovuta a 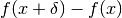$f(x+\delta)-f(x)$ è:

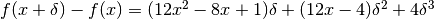
$f(x+\delta)-f(x)=(12x^2-8x+1)\delta+(12x-4)\delta^2+4\delta^3$

Se il tratto è orizzontale, allora la variazione è esattamente nulla, quindi

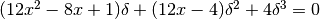
$(12x^2-8x+1)\delta+(12x-4)\delta^2+4\delta^3=0$

Sappiamo (v. 9.4) che la somma di più infinitesimi è indistinguibile da quello di ordine inferiore, perciò l’equazione precedente si riduce a:

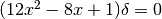
$(12x^2-8x+1)\delta =0$

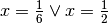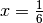che può essere vera solo per $x=\frac{1}{6} \lor x=\frac{1}{2}$ . Il secondo valore si scarta perché non è nell’intervallo delle possibili soluzioni. Quindi la scatola ottimale si costruisce eliminando dagli angoli del foglio 4 quadretti di lato $x=\frac{1}{6}$ rispetto al lato del foglio.

Risolvo con gli iperreali e la geometria¶

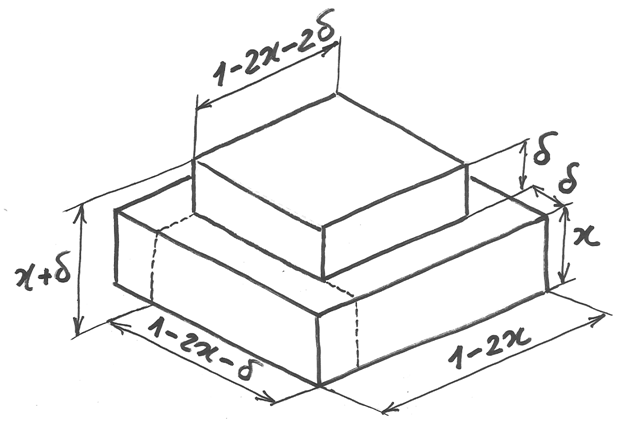
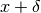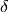Si ottengono le stesse conclusioni immaginando l’aumento di volume che si ottiene con un taglio di quadretti di lato $x+\delta$ , cioè più profondo di $\delta$ rispetto al taglio precedente x.

Se il taglio è più profondo di $\delta$ , l’aumento di volume è infinitesimo.

Se l’aumento di volume è infinitesimo, il nuovo volume è indistinguibile dal precedente.

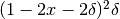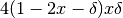Dopo la piegatura, la scatola risulta più alta e più stretta di base. In altezza guadagna un volume pari a $(1-2x-2\delta)^2\delta$ ma perde alla base 4 parallelepipedi di volume complessivo $4(1-2x-\delta)x\delta$ . Solo se stiamo raggiungendo il volume massimo, le variazioni di volume sono pressoché nulle, cioè il nuovo volume è indistinguibile dal precedente. Quindi possiamo pensare che valga:

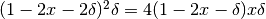
$(1-2x-2\delta)^2\delta=4(1-2x-\delta)x\delta$

che potremmo riscrivere, facendo uso degli indistinguibili:

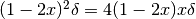
$(1-2x)^2\delta=4(1-2x)x\delta$

Avendo detto che 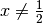$x \ne \frac{1}{2}$ , si può semplificare l’equazione e si ottiene:

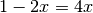
$1-2x=4x$

da cui la soluzione.