Iperreali e 4 operazioni¶
Abbiamo inventato delle grandezze infinitesime e infinite, abbiamo inventato degli strumenti mentali che permettono di vederle in una nuova retta dei numeri, la retta iperreale. Ma chi ci dice che queste cose possano essere considerate dei numeri?
Per potersi fregiare del titolo di numeri devono essere in grado di sostenere le operazioni e magari anche il confronto.
Iperreali: chi sono, quanti sono e come chiamarli¶
Intendiamo per segmento infinitesimo “un segmento piccolo a piacere”, cioè un segmento più piccolo di qualunque segmento di lunghezza finita che possiamo immaginare. Una tale qualità, non può avere alcun multiplo che supera qualsiasi segmento di misura finita, per quanto piccola.
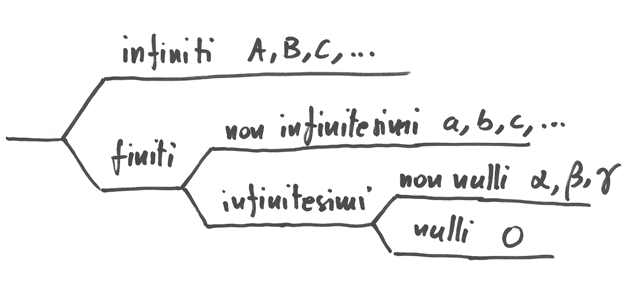
Abbiamo chiamato standard i segmenti e i numeri che abbiamo sempre usato: i segmenti che hanno misura finita e i numeri finiti. I segmenti e i numeri infinitesimi o infiniti sono non standard. D’ora in poi ci riferiamo ai numeri e tralasciamo di specificare ogni volta le proposizioni analoghe relative ai segmenti. Possiamo sintetizzare alcuni fatti:
- Un numero infinitesimo è minore, in valore assoluto, di qualsiasi numero standard positivo.
- Un numero è finito se è minore di almeno un numero standard. Quindi tutti gli standard sono finiti. Per lo stesso motivo, anche gli infinitesimi sono finiti.
- Un numero standard non può essere infinito. Ai numeri standard si applica il postulato di Eudosso Archimede: quindi un numero infinito non è standard e la sua esistenza nega il postulato.
- Un numero infinito è maggiore, in valore assoluto, di qualunque numero standard.
- Lo zero è minore di qualsiasi numero standard positivo. È quindi un numero particolare: è l’unico numero standard infinitesimo.
Dunque i numeri finiti possono essere o no infinitesimi: i numeri finiti non infinitesimi non sono nè infiniti nè infinitesimi, quindi si collocano, per il valore assoluto, fra due numeri standard positivi.
Tutti i numeri standard sono finiti e, a parte lo zero, non infinitesimi. Ma non tutti i finiti non infinitesimi sono numeri standard, pur escludendo 0.
Quanti sono i numeri non standard?¶
Se ammettiamo l’esistenza anche di un solo numero infinitesimo, non possiamo
che ammetterla di tutti: saranno i risultati delle 4 operazioni, svolte fra
infinitesimi e standard.
I reciproci dei numeri infinitesimi (per es.
 )
produrranno numeri infiniti. Infatti, in quanto infinitesimo, sarà:
)
produrranno numeri infiniti. Infatti, in quanto infinitesimo, sarà:
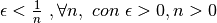 ,
(n finito).
,
(n finito).
Passando ai reciproci e ricordando che la disuguaglianza vale per tutti
gli n, si deduce che
 è un numero infinito.
Se è vero che si possono pensare infiniti numeri infinitesimi, allora,
da questi, potremo ottenere infiniti numeri infiniti,
ricorrendo a disuguaglianze analoghe alla precedente.
è un numero infinito.
Se è vero che si possono pensare infiniti numeri infinitesimi, allora,
da questi, potremo ottenere infiniti numeri infiniti,
ricorrendo a disuguaglianze analoghe alla precedente.
Come indichiamo gli Iperreali?¶
Possiamo ricapitolare i nuovi numeri con la seguente classificazione:
Riguardo ai nomi, in questo testo utilizzeremo le seguenti convenzioni:
| numero | abbreviazione | simboli |
|---|---|---|
| Infinitesimo | i | |
| Infinitesimo non nullo | inn |  |
| Finito | f | |
| Finito non infinitesimo | fni | 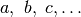 |
| Infinito | I | 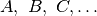 |
| Numero qualunque | 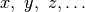 |
La somma¶
La somma fra due numeri
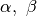 (di tipo inn) non può dare un numero finito.
Si tratta infatti di due quantità infinitesime, più piccole
di qualsiasi numero finito, più piccole anche della sua metà.
Sicché, sommate, non possono superare un qualsiasi valore finito.
Potrebbero però sommare 0, se fossero numeri opposti.
Quindi
(di tipo inn) non può dare un numero finito.
Si tratta infatti di due quantità infinitesime, più piccole
di qualsiasi numero finito, più piccole anche della sua metà.
Sicché, sommate, non possono superare un qualsiasi valore finito.
Potrebbero però sommare 0, se fossero numeri opposti.
Quindi 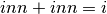 .
.
La somma fra
 e
e  (
(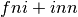 )
aggiunge una quantità piccola a piacere ad un numero finito.
È come se aggiungesse “poco o nulla”, quindi il risultato è fni.
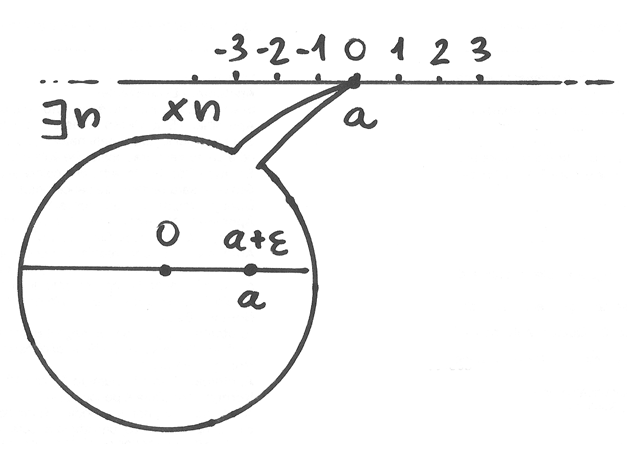
Il caso particolare, che a sia finito, molto piccolo e vicino a zero,
si visualizza con gli opportuni ingrandimenti.
Esiste sempre almeno un ingrandimento
)
aggiunge una quantità piccola a piacere ad un numero finito.
È come se aggiungesse “poco o nulla”, quindi il risultato è fni.
Il caso particolare, che a sia finito, molto piccolo e vicino a zero,
si visualizza con gli opportuni ingrandimenti.
Esiste sempre almeno un ingrandimento
 utile far sì che un microscopio standard visualizzi un simile fni,
proprio perché è diverso da
utile far sì che un microscopio standard visualizzi un simile fni,
proprio perché è diverso da  .
Invece, trattandosi di un microscopio standard, il suo campo visivo non
riesce a cogliere una quantità infinitesima.
E così abbiamo per tutti i casi:
.
Invece, trattandosi di un microscopio standard, il suo campo visivo non
riesce a cogliere una quantità infinitesima.
E così abbiamo per tutti i casi: 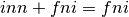 .
.
La somma 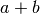 fra due fni propone vari casi: se
fra due fni propone vari casi: se
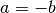 , allora
, allora
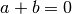 . Se sono di segno concorde risulterà un numero s di tipo
fni.
Se
. Se sono di segno concorde risulterà un numero s di tipo
fni.
Se  , oppure
, oppure 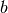 , o entrambi sono fni (nel senso che almeno uno
dei due risulta da
, o entrambi sono fni (nel senso che almeno uno
dei due risulta da
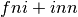 , come visto nel caso precedente) allora può
risultare un inn.
Riassumendo:
, come visto nel caso precedente) allora può
risultare un inn.
Riassumendo: 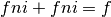 .
.
La tabella sintetizza i possibili casi. Come esempio di un
risultato inatteso, supponiamo che M provenga da una somma

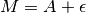 e B sia l’opposto di A:
e B sia l’opposto di A:
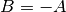 Allora
Allora
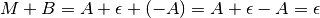 ,
quindi in questo caso:
,
quindi in questo caso: 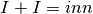
La differenza¶
Le regole della differenza sono legate a quelle della somma;
basta immaginare che il sottraendo sia l’opposto di un
addendo:
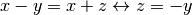 .
.
Vale quindi ancora la stessa tavola di risultati vista per la somma.
Il prodotto¶
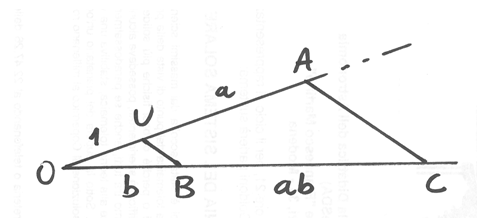
C’è un modo per visualizzare il prodotto fra due numeri come segmento sulla retta: bisogna ricorrere al Teorema di Talete e immaginare i due numeri e l’unità di misura rappresentati come nel disegno.
Riferendosi alle misure (segmenti standard): ab misura BC ed è il prodotto fra le misure dei due segmenti UA e OB. La rappresentazione non cambia sulla retta iperreale, dove, in più, si visualizzano anche le quantità infinitesime.
Immaginiamo il prodotto
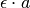 ,
con i punti U e A talmente vicini sulla stessa retta da potersi distinguere
solo con un microscopio non standard.
Allora per il Teorema di Talete B risulterà così vicino a C da richiedere
l’uso di un altro microscopio non standard per distinguerli,
segno evidente che il prodotto è di tipo inn.
,
con i punti U e A talmente vicini sulla stessa retta da potersi distinguere
solo con un microscopio non standard.
Allora per il Teorema di Talete B risulterà così vicino a C da richiedere
l’uso di un altro microscopio non standard per distinguerli,
segno evidente che il prodotto è di tipo inn.
Anche moltiplicare un infinito per un infinitesimo non nullo richiede qualche riflessione. Per es.
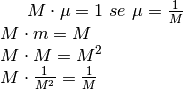
Per un prodotto del tipo
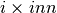 ,
e in assenza di ulteriori informazioni, non è possibile prevedere il tipo
del risultato.
Questi casi, che si verificano anche nella somma, si chiamano forme
indeterminate. Vale comunque:
,
e in assenza di ulteriori informazioni, non è possibile prevedere il tipo
del risultato.
Questi casi, che si verificano anche nella somma, si chiamano forme
indeterminate. Vale comunque:
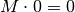
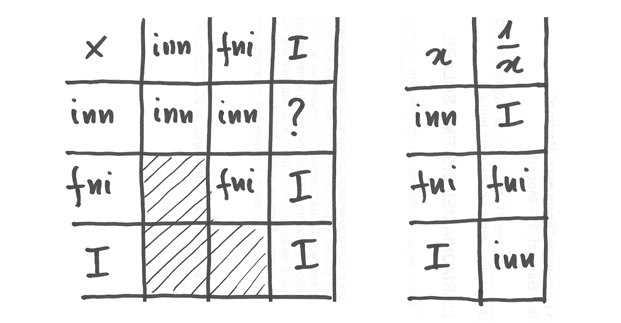
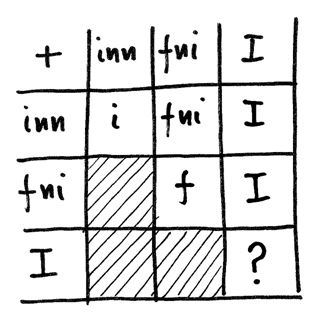
La tabella, che contiene anche casi più facili (per es. il prodotto fra due numeri fni), è la seguente.
Il quoziente¶
La seconda tabella nella Figura 6.6 elenca i tipi dei numeri reciproci di numeri iperreali. È utile per applicare alla divisione le stesse regole del prodotto. Dalla tabella è escluso lo zero, dato che il reciproco di zero non è definito.
Un esempio: dato che
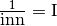 allora
allora
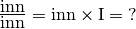
che è un caso indeterminato, come si è già visto nel prodotto.
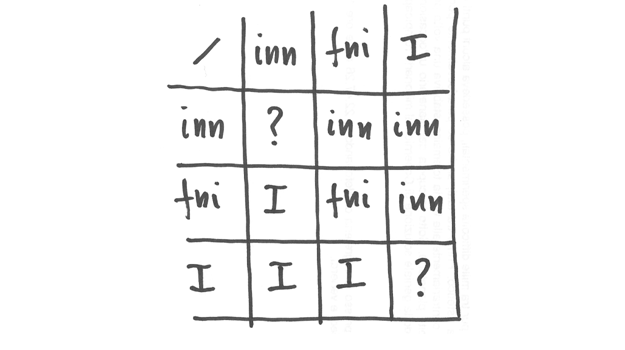
Il quoziente fra un inn e un fni è intuitivamente un infinitesimo. Lo si può dimostrare, ricorrendo alla tabella dei reciproci:
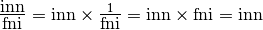
Per il quoziente fra un inn e un I:
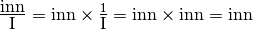
Si possono considerare i reciproci nell’uguaglianza precedente, e ricavare:
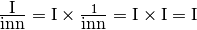 ,
,
oppure, pescando direttamente dalla tabella dei reciproci:
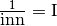
Aiutandosi sempre con la tabella dei reciproci, è facile trovare i tipi risultanti dai quozienti fra un tipo I con un inn oppure con un fni. Infine nello stesso modo regoleremo il rapporto fra un I e un I, che risulta indeterminato. La tabella riassume tutti questi ragionamenti intuitivi
Le dimostrazioni¶
Come provare in modo esatto e formale che queste regole sono coerenti con le
definizioni date ai numeri iperreali?
Per dimostrare i casi nelle tabelle della somma e della differenza per lo più
si ricorre alla disuguaglianza triangolare
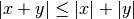 ,
come viene proposto in uno degli esercizi.
,
come viene proposto in uno degli esercizi.
Per gli altri casi, dimostriamo come esempio che il quoziente fra un fni e un
inn è I, cioè è maggiore di qualsiasi standard (s).
Consideriamo per semplicità solo numeri positivi.
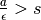 .
Se a è standard è sicuramente maggiore di un altro numero standard t.
Quindi
.
Se a è standard è sicuramente maggiore di un altro numero standard t.
Quindi
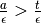 .
Perché quest’ultimo sia
.
Perché quest’ultimo sia
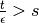 è sufficiente che
è sufficiente che
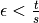 ,
cosa senz’altro vera.
,
cosa senz’altro vera.
Le dimostrazioni formali possono confortare, ma è indispensabile raggiungere i risultati intuitivamente, per valutare con sicurezza e in modo spedito casi più complessi di questi, che sono elementari.
L’ordinamento¶
Per quanto riguarda l’ordinamento possiamo osservare che:
- i numeri negativi sono minori dei numeri positivi;
- i numeri negativi con valore assoluto maggiore sono minori dei numeri negativi con valore assoluto minore;
- 0 è minore di tutti i numeri positivi;
- Gli infinitesimi sono minori di tutti i finiti non infinitesimi positivi;
- i finiti non infinitesimi sono minori degli infiniti positivi;
- tra i finiti non infinitesimi diremo che
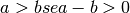 .
.
Riferendoci ai numeri positivi e usando le convenzioni precedenti possiamo scrivere:
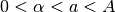
Rimangono da confrontare infinitesimi con infinitesimi e infiniti con infiniti.
Sulle proprietà¶
Le proprietà delle operazioni nell’insieme dei reali valgono anche con gli iperreali. La dimostrazione di questo si deve al matematico Abraham Robinson, che la pubblicò nel 1963.
Riassumendo¶
Standard, non standard, finiti, infiniti e infinitesimi sezionano l’insieme degli Iperreali in vari sottoinsiemi che è indispensabile ricordare. Usando l’intuizione, più che le dimostrazioni formali, si studiano i tipi dei possibili risultati delle 4 operazioni, quando si usano i numeri iperreali. Le operazioni hanno le stesse proprietà che hanno con i numeri reali.
Esercizi¶
- Perché frazionando un segmento finito non riesci mai a ottenere una lunghezza infinitesima?
- Un numero irrazionale è un numero finito? E un numero trascendente? E un numero decimale periodico? E un numero standard può essere decimale illimitato non periodico?
- Se l’insieme dei numeri reali è (già) denso, come è possibile inserire anche gli infiniti e gli infinitesimi? Allora sarà denso anche l’insieme degli iperreali?
- Una tribù primitiva conosce solo l’uso di 4 numeri: 1, 2, 3, 4. Un numero
maggiore viene genericamente indicato con “molti” (5 pecore –>
molte pecore, 8, 15, 30 pecore –> molte pecore).
Immagina che da un gruppo di pecore ne vengano rubate alcune e indica
le sottrazioni e i risultati con questo esiguo insieme di numeri.
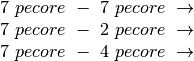
- Classifica con diagrammi di Eulero-Venn l’insieme degli Iperreali, dei numeri finiti, degli infinitesimi, dei numeri standard.
- Completa la casistica dei risultati inattesi per la somma
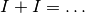 .
. - Visualizza con microscopi e telescopi la somma
 , supponendo a molto minore di 0.
, supponendo a molto minore di 0. - Spiega con esempi la Tavola delle somme.
- Visualizza con microscopi e telescopi 6 esempi diversi di prodotto
- Spiega con esempi la Tavola dei reciproci.
- Dimostra che
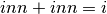 , seguendo il ragionamento
del testo e facendo uso della disuguaglianza triangolare.
, seguendo il ragionamento
del testo e facendo uso della disuguaglianza triangolare. - La Tavola della divisione ha un risultato in ogni casella, non come le precedenti. Perché?
- Abbiamo definito i numeri standard, gli infinitesimi e gli infiniti. Possiamo dire che gli ultimi due fra questi sono non standard e che gli standard sono numeri finiti?
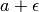 .
.
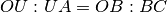
 .
.