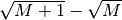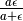Operare con gli indistinguibili¶
Il vantaggio di usare numeri indistinguibili¶
I numeri indistinguibili sono vantaggiosi nel semplificare i calcoli con gli iperreali. L’idea che si segue è di sostituire i numeri dati in un’espressione con altri indistinguibili, con i quali il calcolo risulta più facile. Si otterrà un risultato indistinguibile dal risultato dell’espressione iniziale. In effetti è questo il metodo seguito per risolvere intuitivamente i problemi introduttivi, nei quali il risultato cercato corrisponde alla parte standard dell’espressione risolvente. Ora però vogliamo definire poche regole generali in modo che quel metodo sia applicabile generalmente.
Per iniziare¶
Dal capitolo precedente richiamiamo poche regole pratiche. Diremo che:
- nella somma di due infinitesimi posso trascurare un
infinitesimo di ordine superiore, es:
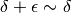 , se
, se
 è di ordine superiore;
è di ordine superiore; - nella somma di un finito non infinitesimo con un infinitesimo posso
trascurare l’infinitesimo, es:
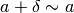 ;
; - nella somma di un infinito con un finito posso trascurare il finito, es:
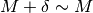 e
e 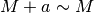 ;
; - nella somma di due infiniti posso trascurare un infinito di
ordine inferiore, es:
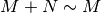 se
se 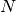 è di ordine inferiore.
è di ordine inferiore.
Esempi di calcoli¶
Trovare il tipo di
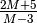 e, se si tratta di un numero
finito, la sua parte standard.
e, se si tratta di un numero
finito, la sua parte standard.Si tratta di un rapporto fra infiniti, quindi una forma indeterminata. Con le regole degli indistinguibili si ottiene
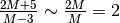 .
È un numero di tipo f, quindi
.
È un numero di tipo f, quindi
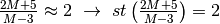 .
.Analogamente, si ottiene:
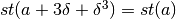 perché
l’espressione indistinguibile corrispondente a quella data è a.
perché
l’espressione indistinguibile corrispondente a quella data è a.Con stessa facilità si può vedere che
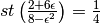 .
.Una situazione da analizzare con cura:
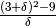 Se si opera pensando che la parentesi sia indistinguibile da 3, allora
il numeratore è indistinguibile da 0. Ma la definizione di
indistinguibili dice: Due numeri non nulli si dicono.... Quindi se uno dei
numeri è 0 non si può ricorrere agli indistinguibili. Operando algebricamente
si evita l’ostacolo.
Se si opera pensando che la parentesi sia indistinguibile da 3, allora
il numeratore è indistinguibile da 0. Ma la definizione di
indistinguibili dice: Due numeri non nulli si dicono.... Quindi se uno dei
numeri è 0 non si può ricorrere agli indistinguibili. Operando algebricamente
si evita l’ostacolo.
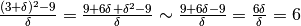 ,
cioè la frazione è indistinguibile da 6.
,
cioè la frazione è indistinguibile da 6.
Ma come ci si comporta in generale di fronte a un problema simile?
Somme algebriche fra indistinguibili¶
Come mi devo comportare se devo sommare o sottrarre due iperreali? La loro somma (o differenza) può essere ricavata attraverso la somma (o differenza) dei loro indistinguibili? In simboli:
Dati 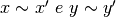 , è vero che:
, è vero che: 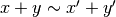 ?
?
La risposta è: non in tutti i casi. Se x, y sono due numeri indistinguibili
fra loro (quindi se vale anche 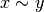 ) allora:
) allora:
- se devo sommarli, non devono essere numeri opposti
- se devo sottrarli, non posso usare gli indistinguibili al loro posto.
Esempi di calcoli e di rappresentazioni¶
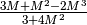 contiene iperreali infiniti. Seguendo le
regole sintetizzate in apertura, si trascurano gli infiniti di ordine
inferiore. Quindi:
contiene iperreali infiniti. Seguendo le
regole sintetizzate in apertura, si trascurano gli infiniti di ordine
inferiore. Quindi:
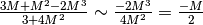 .
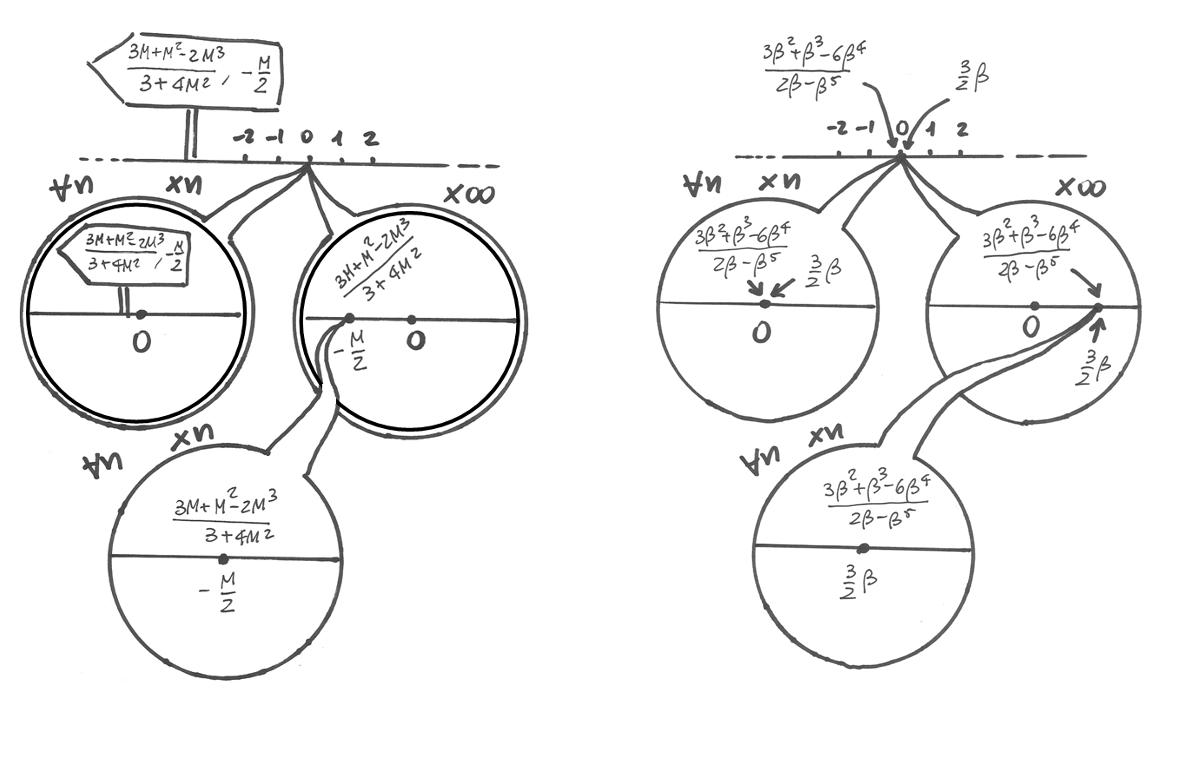
La rappresentazione mostra che qualsiasi zoom standard non può visualizzare
i due numeri sulla retta disegnata in scala ordinaria. Invece con uno zoom
non standard i due numeri entrano nel campo visivo e sembrano coincidere.
Per separarli occorrerà usare un microscopio non standard. Questo conferma
la definizione del cap. precedente: la distanza fra indistinguibili
non può essere visualizzata nella stessa scala in cui compaiono sulla retta.
.
La rappresentazione mostra che qualsiasi zoom standard non può visualizzare
i due numeri sulla retta disegnata in scala ordinaria. Invece con uno zoom
non standard i due numeri entrano nel campo visivo e sembrano coincidere.
Per separarli occorrerà usare un microscopio non standard. Questo conferma
la definizione del cap. precedente: la distanza fra indistinguibili
non può essere visualizzata nella stessa scala in cui compaiono sulla retta.- In
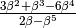 si trascurano
gli infinitesimi di ordine superiore. Il risultato è un infinitesimo
(quindi ha la parte standard nulla) e lo si vede in figura 2.
Sulla retta i numeri coincidono con 0 nel campo visivo di qualsiasi
microscopio standard, coincidono fra loro (ma distinti da 0) nel campo
visivo di un microscopio non standard e restano indistinti anche applicando
un qualsiasi ulteriore microscopio standard.
si trascurano
gli infinitesimi di ordine superiore. Il risultato è un infinitesimo
(quindi ha la parte standard nulla) e lo si vede in figura 2.
Sulla retta i numeri coincidono con 0 nel campo visivo di qualsiasi
microscopio standard, coincidono fra loro (ma distinti da 0) nel campo
visivo di un microscopio non standard e restano indistinti anche applicando
un qualsiasi ulteriore microscopio standard.
Esercizi svolti¶
Trova gli indistinguibili delle espressioni seguenti.
Soluzioni:
se considero
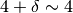 il risultato della
parentesi è 0. Poiché lo zero è escluso dalla relazione di
indistinguibilità, devo sviluppare la differenza:
il risultato della
parentesi è 0. Poiché lo zero è escluso dalla relazione di
indistinguibilità, devo sviluppare la differenza:
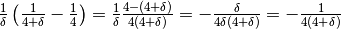 Ora posso applicare l’indistinguibilità.
Ora posso applicare l’indistinguibilità.
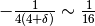
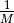 è un infinitesimo ma non posso trascurarlo nella
parentesi tonda per gli stessi motivi dell’es.1. Devo svolgere i calcoli
e poi cercare gli indistinguibili.
è un infinitesimo ma non posso trascurarlo nella
parentesi tonda per gli stessi motivi dell’es.1. Devo svolgere i calcoli
e poi cercare gli indistinguibili.
![M\left[\left(4+\frac{1}{M}\right)^2-16\right]=
M\left[16+\frac{8}{M}+\frac{1}{M^2}-16\right]=
M\left(\frac{8}{M}+\frac{1}{M^2}\right)=8+\frac{1}{M}\sim 8](../../../_images/math/f337c4f9cd1f0761e959078972c4b255e0055d62.png)
Trascurando 1 nel primo radicando, si ricade nel problema dello zero. Si ricorre allora ad un trucco algebrico: moltiplicare e dividere per la stessa quantità nel modo seguente:
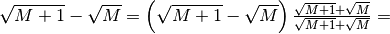
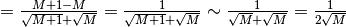
L’ultima espressione rappresenta un infinitesimo e quindi:
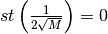
Guardando il denominatore, è facile ricavare che la frazione è indistinguibile da un infinitesimo e quindi la sua parte standard è nulla.
Riassumendo¶
L’uso degli indistinguibili è vantaggioso per semplificare i calcoli. Nello svolgere gli esercizi l’unica cautela è evitare che l’espressione si annulli e per questo si ricorre alle tecniche dell’algebra.
Esercizi¶
- Considera
 . Dimostra:
a)
. Dimostra:
a) 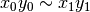 ;
b)
;
b) 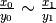
- Considera
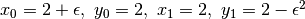 e
dimostra che vale come esempio per la regola della differenza fra
indistinguibili.
e
dimostra che vale come esempio per la regola della differenza fra
indistinguibili. - Trova l’indistinguibile:
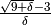
- Trova l’indistinguibile:
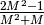
- Trova l’indistinguibile:
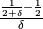
- Trova l’indistinguibile:
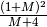
- Trova l’indistinguibile:
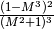
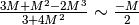 (un infinito) e
(un infinito) e
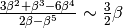 (un infinitesimo).
(un infinitesimo).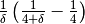
![M\left[\left(4+\frac{1}{M}\right)^2-16\right]](../../../_images/math/e411420ba8caf46255ce562d3c3ea595856d3a17.png)