Il percorso minimo

Il secondo esempio è un problema classico, brillantemente risolto da Erone. Noi ricaveremo la soluzione esatta usando gli infinitesimi e visualizzandola con i microscopi.

Il problema

Trova il tragitto minimo per andare da A a B toccando una volta la retta.

Percorsi maggiori:

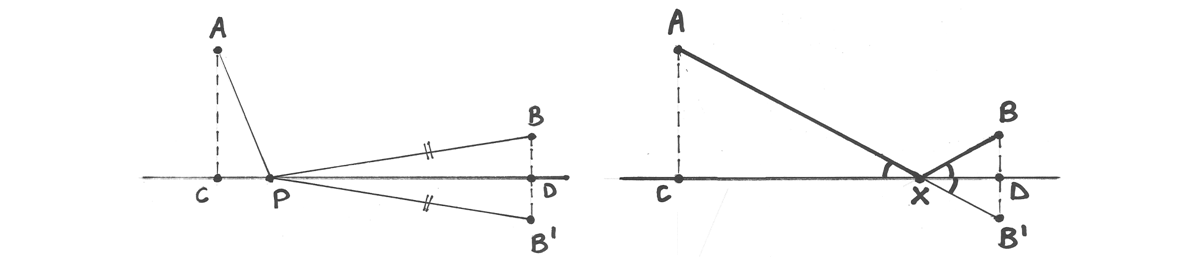
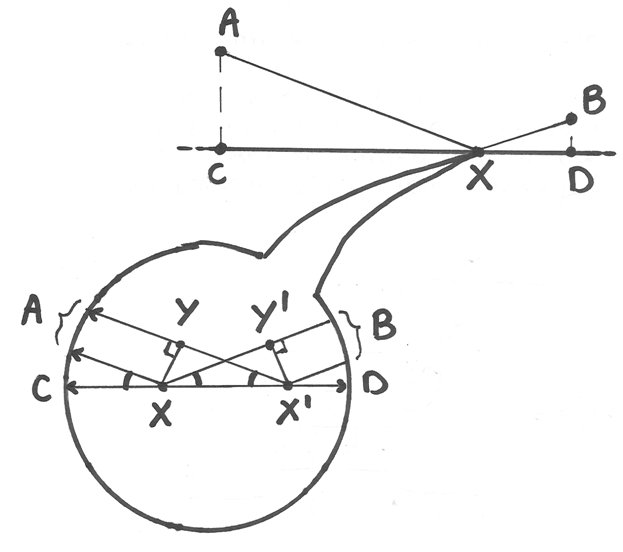
Da un primo esame risulta ovvio che i tragitti APB sono minori se P appartiene al segmento CD, che ha per estremi le proiezioni di A e di B sulla retta.

Percorsi minori:

Infatti nella figura 1 è facile confrontare AP con AC e PB con BC nel primo disegno, e analogamente nel secondo disegno della figura 1. Meno facile è indicare quale sia la migliore posizione di P all’interno del segmento CD, anche se è chiaro che se si trovasse agli estremi il percorso non sarebbe il minimo (figura 2).

La soluzione geometrica

Una soluzione semplice ed elegante ci viene dalla geometria

Soluzione geometrica: PB = PB’

Se costruiamo un triangolo PDB’ simmetrico di PDB rispetto alla retta, abbiamo che PB = PB’. Quindi possiamo analizzare la lunghezza del percorso AP + PB’ al posto di AP + PB, perché si tratta di due spezzate di uguale misura. Ora, fra tutte le spezzate possibili APB’, quella più breve è il segmento AB’: l’intersezione X fra il segmento e la retta è la posizione cercata. La caratteristica di questa posizione è che gli angoli disegnati in X sono tutti uguali. Quindi la soluzione è: il punto X sulla retta è tale da formare angoli uguali fra la retta e i due segmenti che formano la spezzata AXB.

La soluzione analitica

Se potessimo mettere in grafico la funzione che descrive la lunghezza del percorso APB, potremmo vedere che la funzione ha il valore minimo in corrispondenza del punto X ottimale, perché ogni altro percorso è maggiore.

Grafico della f risolvente: X è punto di minimo.

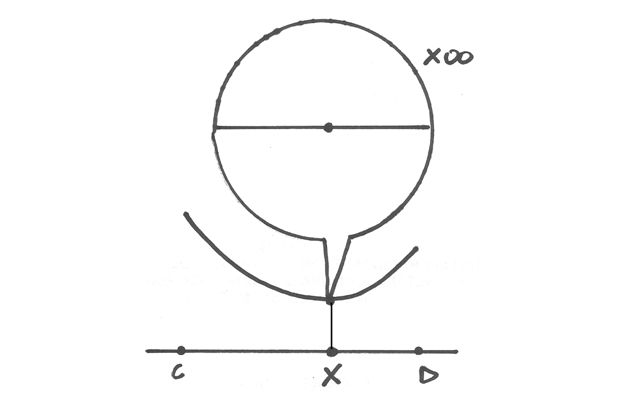
Puntando un microscopio non standard su X (ancora non calcolato), vediamo che il grafico appare nel campo visivo come un segmento orizzontale. Nella monade di X, qualsiasi altro punto X’ genera una misura della spezzata (e quindi un punto del grafico) diversa per ordini di grandezza superiori alla differenza XX’, quindi indistinguibile da quella calcolata per X. Possiamo perciò assumere che la differenza fra le lunghezze delle due spezzate AXB e AX’B sia nulla.

Cammini indistinguibili: AX’+X’B=AX+XB

Approfondiamo il dettaglio ingrandendo la posizione di X in modo che sia distinto da X’. Nel campo visivo avremo coppie di segmenti indistinguibili da segmenti paralleli (AX con AX’ e BX con BX’). In realtà non sono paralleli, ma la differente inclinazione non risulta a questa scala di ingrandimento. Se vale il parallelismo, siamo nella condizione di minimo percorso, perché i triangoli XX’Y e XX’Y’ sono congruenti, quindi il tratto in più del segmento AX’ uguaglia il tratto in più del segmento XB. Inoltre, sempre per il parallelismo, sono congruenti gli angoli che si trovano sulla retta, con vertice X e X’.

La riflessione della luce

Al posto di questi angoli, si possono considerare quelli formati dalla normale in X con i due segmenti AX e BX, che sono congruenti in quanto complementari degli angoli precedenti. In questa descrizione, se r rappresenta una superficie riflettente e la spezzata rappresenta il percorso di un raggio luminoso, ecco che abbiamo ricavato la legge della riflessione nell’ottica geometrica.

In questo modo possiamo concludere che il raggio di luce nella riflessione percorre il cammino minimo.