Uso degli infinitesimi e degli infiniti¶
Il calcolo infinitesimale fa uso di quantità infinitamente piccole, o infinitesime, e di quantità infinitamente grandi, o infinite. Dovremo quindi ricorrere a un insieme di numeri che comprenda numeri infinitesimi e numeri infiniti: i numeri iperreali. Prima di introdurre i numeri iperreali affrontiamo in modo informale alcuni problemi in modo da entrare nello spirito del calcolo infinitesimale.
Ascissa del vertice della parabola¶
Cominciamo da un problema molto semplice di cui conoscete già la soluzione:
Determinare l’ascissa del vertice
della parabola di equazione 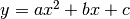 .
.
Per altre vie abbiamo imparato che l’ascissa del vertice è:
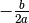 ,
ma ora vogliamo provare a ottenere lo stesso risultato usando quantità
infinitesimali.
,
ma ora vogliamo provare a ottenere lo stesso risultato usando quantità
infinitesimali.
Supponiamo di poter usare quantità infinitamente piccole e di avere a disposizione un potentissimo microscopio col quale visualizzarle. Se puntiamo il nostro microscopio su un punto della parabola, ecco che il grafico risulta indistinguibile da un segmento rettilineo. Se puntiamo il microscopio in diversi punti del grafico, l’immagine al microscopio sarà quella di un segmento con una pendenza variabile.
La pendenza di un segmento nel piano cartesiano abituale è
data dal rapporto fra l’incremento delle ordinate e
l’incremento delle ascisse dei suoi estremi
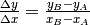 ,
Se il segmento è orizzontale, la sua pendenza è nulla,
cioè non vi è incremento di ordinate (
,
Se il segmento è orizzontale, la sua pendenza è nulla,
cioè non vi è incremento di ordinate (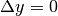 ) e
infatti i valori di ordinata dei due estremi sono uguali.
Ma se immaginiamo di usare quantità infinitesime,
e quindi vediamo il segmento orizzontale grazie al microscopio,
potrebbe succedere di vedere il segmento orizzontale perché il
microscopio, mentre coglie l’incremento delle ascisse
non è così potente da riuscire a cogliere l’incremento delle
ordinate agli estremi.
In questo caso avremmo bisogno di un microscopio più potente
e allora diciamo che l’incremento infinitesimo in ordinata è
di ordine superiore rispetto a quello visualizzato in ascissa.
) e
infatti i valori di ordinata dei due estremi sono uguali.
Ma se immaginiamo di usare quantità infinitesime,
e quindi vediamo il segmento orizzontale grazie al microscopio,
potrebbe succedere di vedere il segmento orizzontale perché il
microscopio, mentre coglie l’incremento delle ascisse
non è così potente da riuscire a cogliere l’incremento delle
ordinate agli estremi.
In questo caso avremmo bisogno di un microscopio più potente
e allora diciamo che l’incremento infinitesimo in ordinata è
di ordine superiore rispetto a quello visualizzato in ascissa.
Il vertice della parabola è caratterizzato dal fatto di essere l’unico punto per il quale il microscopio ci mostra un segmento orizzontale. Usando il linguaggio precedente, questo significa che se ci spostiamo di un tratto infinitesimo dall’ascissa del vertice, allora la variazione di ordinata è un infinitesimo di ordine superiore allo spostamento infinitesimo in ascissa.
Traduciamo le considerazioni precedenti in un calcolo. Sia 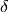 un numero infinitesimo.
un numero infinitesimo.
Calcoliamo ora la variazione di ordinata sulla parabola passando da
 a
a 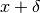 .
L’ordinata corrispondente a
.
L’ordinata corrispondente a 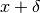 è:
è:
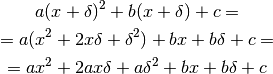
Poiché l’ordinata corrispondente a  è
è 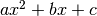 ,
la variazione cercata è:
,
la variazione cercata è:
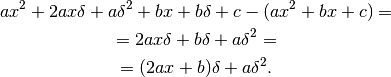
Ma 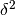 è un infinitesimo di ordine superiore a
è un infinitesimo di ordine superiore a 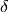 perché rapportato a
perché rapportato a 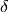 dà:
dà: 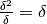 che è un infinitesimo. Dunque
che è un infinitesimo. Dunque 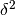 è un infinitesimo anche
rispetto a
è un infinitesimo anche
rispetto a 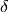 .
L’ascissa del vertice della parabola sarà allora quel numero
.
L’ascissa del vertice della parabola sarà allora quel numero  per il quale la variazione di ordinata,
per il quale la variazione di ordinata, 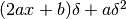 ,
conterrà soltanto il termine
,
conterrà soltanto il termine 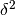 .
Deve essere quindi
.
Deve essere quindi 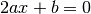 da cui:
da cui: 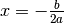 .
.
Tangente a una parabola¶
Passiamo ora ad un altro problema: trovare l’equazione della retta tangente
alla parabola 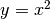 nel punto di ascissa
nel punto di ascissa 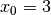 .
A volte per brevità viene definita la tangente come quella retta che ha in
comune con la curva un solo punto. Ma questa definizione non è soddisfacente
in generale. In certi casi una retta può essere tangente ad una curva in un
punto e intersecarla in altri punti.
Possiamo risolvere il problema con il metodo del fascio di rette:
.
A volte per brevità viene definita la tangente come quella retta che ha in
comune con la curva un solo punto. Ma questa definizione non è soddisfacente
in generale. In certi casi una retta può essere tangente ad una curva in un
punto e intersecarla in altri punti.
Possiamo risolvere il problema con il metodo del fascio di rette:
troviamo le coordinate del punto
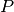 di tangenza:
di tangenza:
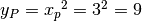
scriviamo l’equazione del fascio di rette passanti per
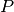 :
:
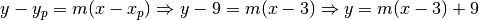
Calcoliamo le intersezioni tra retta e parabola:
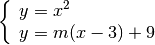
Sostituendo otteniamo l’equazione risolvente:
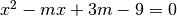
imponiamo che le intersezioni tra la generica retta del fascio e la parabola siano coincidenti cioè che l’equazione risolvente abbia le due soluzioni coincidenti cioè abbia il discriminante uguale a zero:
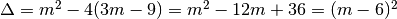
e quindi
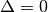 quando
quando 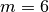
La retta tangente è quindi la retta del fascio che ha pendenza uguale a
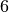 cioè la retta di equazione:
cioè la retta di equazione:
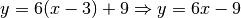
Questo metodo funziona perché la parabola ha un’equazione di secondo grado.
Già per risolvere lo stesso problema con un’equazione di terzo grado,
ad esempio la cubica:
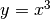 ,
lo stesso metodo non funziona (perché?).
,
lo stesso metodo non funziona (perché?).
Definiamo come retta tangente ad un grafico di una funzione in un suo punto l’unica retta che, nel campo visivo di un microscopio che ci consente di vedere spostamenti infinitesimi, risulta indistinguibile dal grafico della funzione. In termini più precisi, si tratta dell’unica retta per la quale la differenza tra la sua ordinata e l’ordinata del grafico della funzione, calcolata per un valore di ascissa a distanza infinitesima dall’ascissa del punto di contatto, risulta essere un infinitesimo di ordine superiore all’incremento infinitesimo in ascissa.
Ma vediamo di fare il calcolo. Come già visto, una generica retta per il punto
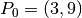 ha equazione
ha equazione
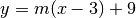 .
Invece del punto di ascissa 3, consideriamo il
punto di ascissa
.
Invece del punto di ascissa 3, consideriamo il
punto di ascissa
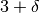 ,
dove
,
dove
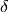 ,
è un numero infinitesimo.
,
è un numero infinitesimo.
Troviamo quanto vale l’ordinata della retta in quel punto.
Sostituiamo a
 il valore
il valore
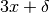 ottenendo:
ottenendo:
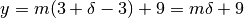
E quanto vale l’ordinata della parabola in quel punto?:
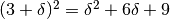 .
.
La differenza delle ordinate vale allora:
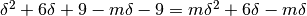 che possiamo scrivere:
che possiamo scrivere:
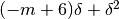
Imponendo che si annulli la parte dello stesso ordine di
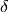 quindi:
quindi:
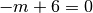 e
e
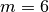
Il risultato è lo stesso ottenuto con l’altro metodo, ma qui non abbiamo utilizzato le equazioni di secondo grado e il discriminante. Questo metodo è più generale e si può applicare, ad esempio, anche alla ricerca di tangenti in parabole di grado superiore.
Possiamo rivedere il problema da un punto di vista leggermente diverso:
possiamo cercare la pendenza di una retta che passa per un punto della parabola
e per un altro punto (sempre della parabola) infinitamente vicino a questo.
Oltre al punto
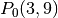 consideriamo il punto
consideriamo il punto
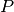 di ascissa
di ascissa
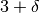 dove
dove
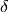 è un infinitesimo.
è un infinitesimo.
L’ordinata di
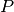 è allora:
è allora:
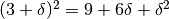 e la pendenza del segmento
e la pendenza del segmento
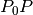 è:
è:
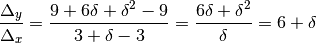
Ma l’unico numero reale a cui il numero
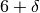 è infinitamente vicino è proprio
è infinitamente vicino è proprio
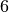 e ritroviamo così lo stesso valore.
e ritroviamo così lo stesso valore.
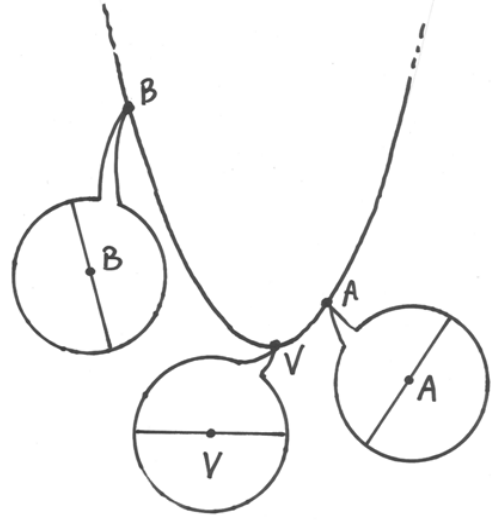
Cerchio osculatore al vertice della parabola¶
La tangente è la retta che meglio approssima una curva in un suo punto. Il cerchio osculatore è la circonferenza che meglio approssima una curva in un suo punto.
Problema: trovare qual è la circonferenza che meglio approssima la parabola:
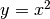 nel suo vertice.
nel suo vertice.
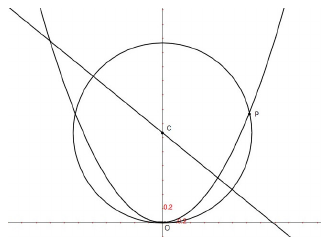
Parabola e circonferenza passante per il vertice. La circonferenza ha centro sull’asse y e sull’asse del segmento OP.
Soluzione: dato che per individuare una circonferenza abbiamo bisogno di 3
punti,
dobbiamo considerare, oltre al punto dato, altri due punti infinitamente
vicini a questo.
Possiamo osservare che, per questioni di simmetria, il centro della
circonferenza starà sull’asse di simmetria della parabola.
Il centro della circonferenza sarà l’intersezione dell’asse del segmento
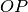 con l’asse
con l’asse
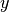 quando il punto
quando il punto
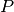 si avvicina infinitamente a al punto
si avvicina infinitamente a al punto
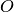 .
.
Il punto
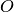 ha coordinate
ha coordinate
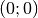 il punto
il punto
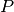 ha ascissa
ha ascissa
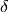 e ordinata
e ordinata
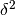
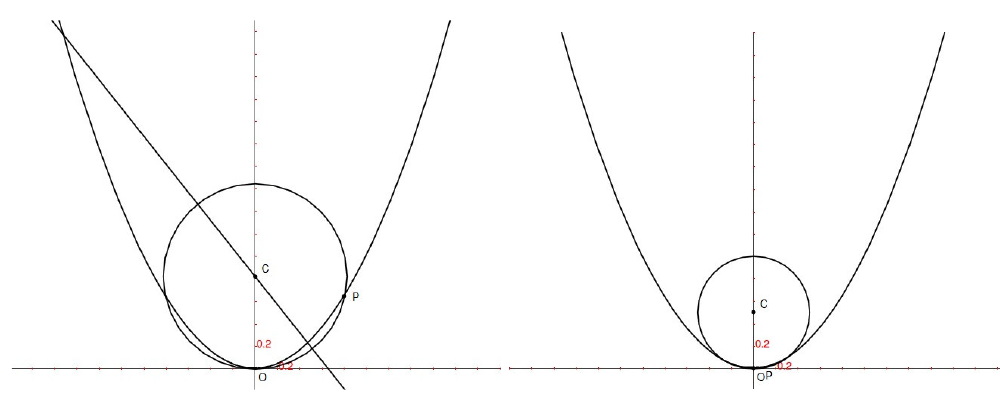
Ricerca del cerchio osculatore. 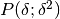 percorre la
parabola avvicinandosi al suo vertice. Individua così una circonferenza di
raggio progressivamente minore.
percorre la
parabola avvicinandosi al suo vertice. Individua così una circonferenza di
raggio progressivamente minore.
Dato che i punti dell’asse del segmento sono equidistanti dagli estremi,
l’equazione dell’asse sarà:
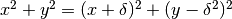 che diventa:
che diventa:
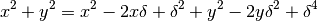
Spostando tutto a primo membro ed eliminando i termini opposti si ottiene:
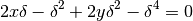
L’intersezione con l’asse
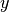 si ottiene ponendo
si ottiene ponendo
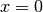 quindi l’equazione diventa
quindi l’equazione diventa
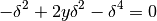
da cui ricavo:
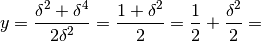
Il valore esatto dell’ordinata del centro è il numero reale che è
infinitamente vicino a questo “numero”.
Ma l’unico numero che è infinitamente vicino a
 più un infinitesimo è proprio
più un infinitesimo è proprio
 Il centro del cerchio osculatore è quindi il punto
Il centro del cerchio osculatore è quindi il punto
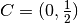 e il suo raggio è
e il suo raggio è
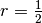 per cui l’equazione della circonferenza è:
per cui l’equazione della circonferenza è:
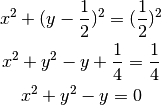
Questo può ricordarci che una porzione limitata di uno specchio sferico si comporta come uno specchio parabolico avente il fuoco a una distanza pari alla metà del raggio.
Riassumendo¶
Usando quantità “infinitesime” possiamo risolvere problemi che sappiamo già risolvere con metodi algebrici. Gli “infinitesimi” forniscono uno strumento più generale che ci permette di risolvere anche problemi che con il metodo algebrico non sapremmo affrontare. Gli “infinitesimi” sarebbero comodi, peccato che non sappiamo se esistono.
Esercizi¶
- Calcola la tangente ad una parabola cubica nel punto
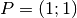 .
. - Calcola le tangenti alle curve:
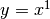 ,
,
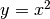 ,
,
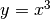 ,
,
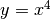 ,
,
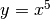 , ...
nel punto:
, ...
nel punto:
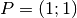 e confrontale tra di loro.
e confrontale tra di loro.