Strumenti per vedere gli iperreali¶
Per poter operare con le grandezze infinitesime e infinite, dobbiamo riuscire a “vederle”. Per visualizzare i numeri reali usiamo la retta, sappiamo infatti che ogni numero reale è in corrispondenza biunivoca con un punto della retta reale. Ma se tutti i punti della retta sono già impegnati con i numeri reali come possiamo rappresentare queste altre grandezze?
Abbiamo bisogno di un nuovo modello di retta che contenga oltre ai punti reali anche i punti corrispondenti a queste nuove grandezze.
Una nuova retta per i nuovi numeri¶
Dobbiamo inventare un’altra retta che possiede altri punti oltre a quelli reali. Creiamo una retta “Iperreale” che oltre ai punti della retta reale ha anche altri punti che corrispondono agli infinitesimi e agli infiniti.
La nuova retta contiene anche i punti della retta reale e chiameremo numeri standard i numeri reali che corrispondono a quei punti e segmenti standard i segmenti di cui i numeri standard, in valore assoluto, esprimono la misura. La novità di questa retta è che su di essa si possono visualizzare i nuovi numeri, oltre ai numeri standard. Ma come facciamo a vederli, dato che tutti i punti normali della retta sono già occupati a rappresentare i numeri reali?
Abbiamo bisogno di alcuni strumenti particolari, che la nostra immaginazione ci può fornire.
Microscopi, telescopi e zoom¶
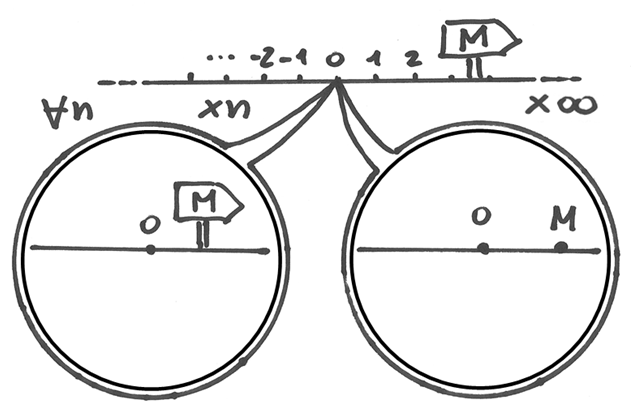
Poiché si tratta di collocare sulla retta iperreale numeri infinitesimi, che rappresentano “posizioni infinitamente vicine” ai numeri standard, e numeri infiniti, che corrispondono a “posizioni infinitamente lontane”, dobbiamo migliorare la nostra capacità di osservare e definire la distribuzione dei numeri sulla la retta iperreale. Per questo useremo microscopi, telescopi e zoom. Iniziamo ad usarli per visualizzare la posizione dei numeri standard.
Visualizzare numeri standard¶
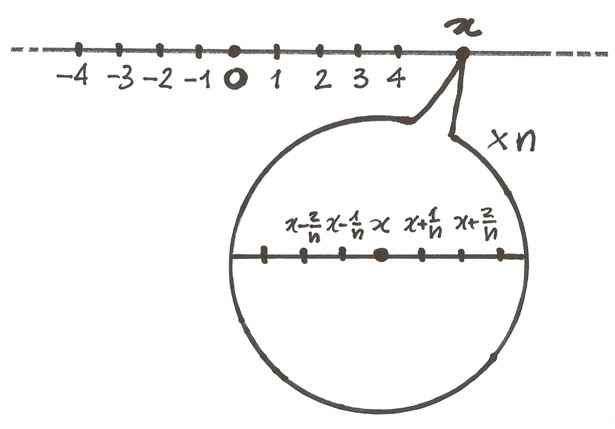
Il microscopio punta la posizione del numero x sulla retta iperreale e ne
ingrandisce i dintorni n volte.
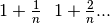 sono i numeri a destra di x (e analogamente a sinistra), distanti da x
multipli di
sono i numeri a destra di x (e analogamente a sinistra), distanti da x
multipli di
 .
Le distanze fra i numeri vicini, ingrandite
al microscopio, appaiono uguali alle distanze nelle zone non ingrandite della
retta, ma in realtà sono distanze n volte minori.
.
Le distanze fra i numeri vicini, ingrandite
al microscopio, appaiono uguali alle distanze nelle zone non ingrandite della
retta, ma in realtà sono distanze n volte minori.
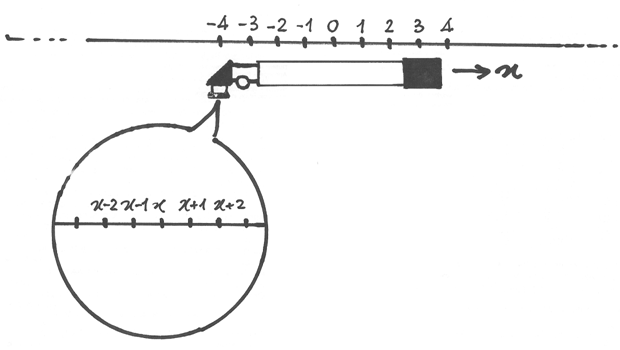
Invece il telescopio non ingrandisce, serve ad “avvicinare” posizioni lontane
sulla retta iperreale. Le distanze fra numeri vicini sono quindi le distanze
consuete.
Per indicare che puntiamo su x scriveremo 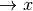
Sono strumenti che si possono usare progressivamente, nel caso si voglia approssimare un numero qualsiasi. Ecco per esempio come puntare ad un numero lontano da 0 e ingrandire i suoi dintorni fino a visualizzarne i dettagli al centesimo di millesimo. Basta applicare un telescopio, puntare al numero intero con questo e poi progressivamente applicare due microscopi (x100 e x1000).
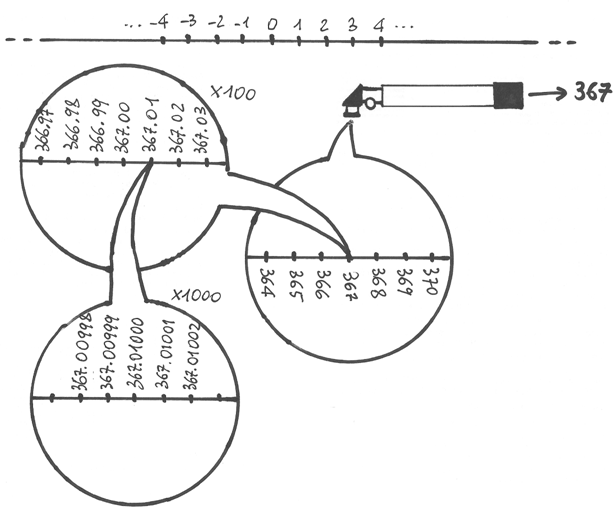
Come organizzarsi per distinguere nel campo visivo le posizioni prossime al numero 367,01000, diverse per la quinta cifra decimale.
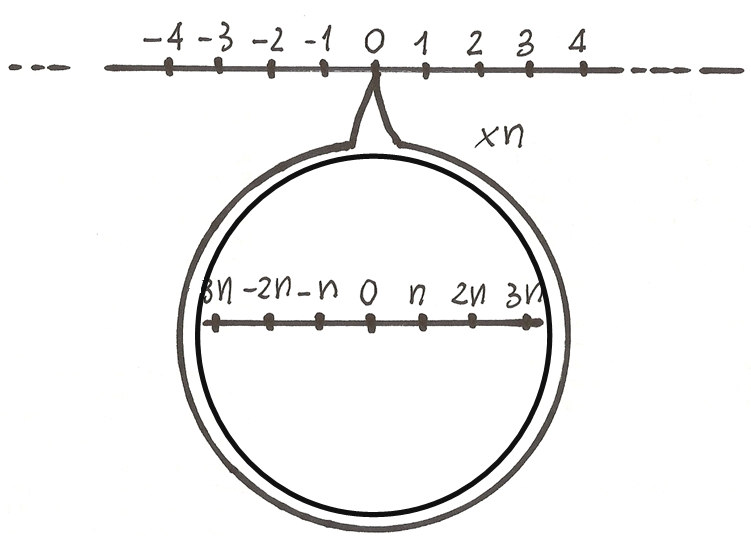
Lo zoom (o grandangolo) è come un microscopio al contrario: le distanze che vengono visualizzate non sono fra unità ordinarie, ma fra loro multipli. Serve a guardare un punto da più lontano e lo punteremo esclusivamente sullo zero. In questo modo vengono visualizzati sia l’origine sia il punto lontano nello stesso campo visivo, ovviamente cambiando la scala di visualizzazione. Nei disegni, lo zoom sembra un microscopio con il bordo doppio.
Visualizzare i non standard¶
Ora che abbiamo fatto un po’ di pratica con i nuovi strumenti puntandoli sui “vecchi” numeri reali, proviamo ad usarli con i nuovi numeri.
In quale posizione della retta si situa un numero infinitesimo
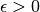 ?
Essendo così piccolo da risultare minore di qualsiasi numero standard,
un infinitesimo non può che situarsi così vicino allo zero da non riuscire a
distinguere i due numeri, con qualsiasi microscopio
(
?
Essendo così piccolo da risultare minore di qualsiasi numero standard,
un infinitesimo non può che situarsi così vicino allo zero da non riuscire a
distinguere i due numeri, con qualsiasi microscopio
(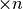 ),
non importa quale ingrandimento sia
impostato (
),
non importa quale ingrandimento sia
impostato (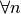 ).
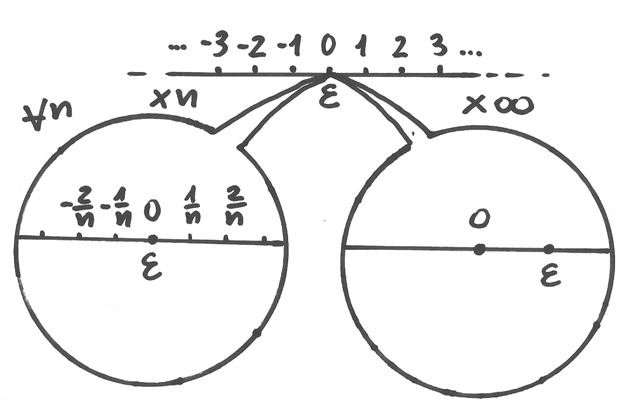
Avremo allora bisogno di un microscopio non standard,
capace di infiniti ingrandimenti (
).
Avremo allora bisogno di un microscopio non standard,
capace di infiniti ingrandimenti (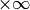 )
)
Analogamente, un numero M infinito,
così grande da superare qualsiasi numero standard,
si situa così lontano dall’origine che nessuno zoom standard
(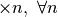 )
lo può visualizzare.
Potrà entrare nel campo visivo solo di uno zoom non standard
(
)
lo può visualizzare.
Potrà entrare nel campo visivo solo di uno zoom non standard
(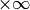 )
)
Riassumendo¶
Per far corrispondere i nuovi numeri ai punti di una retta, non basta la vecchia retta reale, abbiamo bisogno di una nuova retta, una retta Iperreale.
Per poter visualizzare i punti della retta Iperreale possiamo utilizzare tre strumenti mentali: il microscopio, il telescopio, lo zoom.
Esercizi¶
Scrivi 4 numeri che puoi visualizzare puntando il telescopio su:
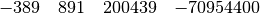
Quanti ingrandimenti deve avere un microscopio se vuoi visualizzare i numeri più vicini a:
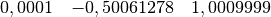
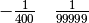
Disegna come combinare gli strumenti per visualizzare

Se disponi solo di microscopi x100 e x1000, come visualizzare la settima cifra decimale di
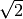 ,
la nona cifra decimale di
,
la nona cifra decimale di
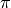 , la quinta cifra
decimale di
, la quinta cifra
decimale di
 ?
?