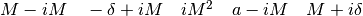Complessi iperreali¶

I punti nel piano iperreale possono rappresentare numeri ipercomplessi, come punti o come vettori, esattamente come succede con i numeri complessi visualizzati nel piano reale. Ci chiediamo: quando un numero ipercomplesso è infinitesimo? Quando è infinito? E quando è finito non infinitesimo? (Mossi i primi passi, tralasceremo l’indicazione “iper” che è ovvia, e parleremo solo di complessi, parti reali e immaginarie, sottintendendo che si tratta di parti iperreali e iperimmaginarie)

Complessi infinitesimi¶

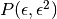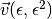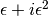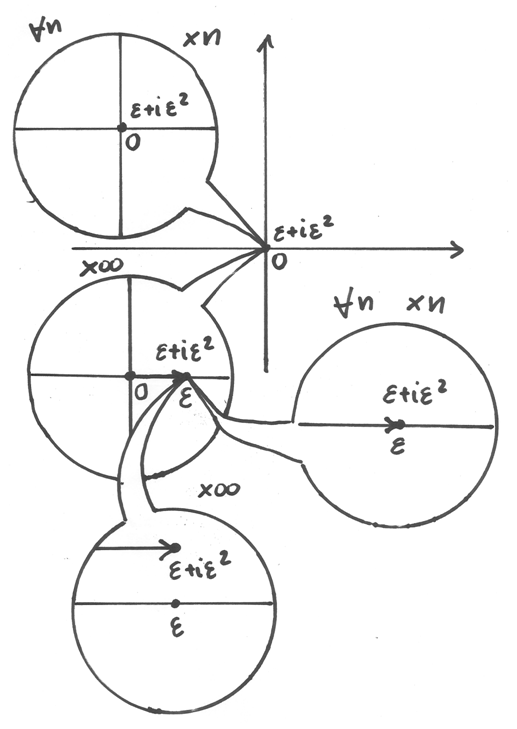
Proviamo a rappresentare nel piano ipercomplesso il punto $P(\epsilon, \epsilon^2)$ o il vettore $\vec v(\epsilon, \epsilon^2)$ , corrispondenti a $\epsilon + i\epsilon^2$ . Immaginiamo positivi tutti gli infinitesimi, per semplificare.

Iperreale complesso infinitesimo $\epsilon + i\epsilon^2$ .

Nella scala ordinaria i punti (1, 0) e (0, 1) sono distinti dall’origine. In questa scala nessun microscopio standard riesce a distinguere dallo zero il nostro numero. Dobbiamo applicare un microscopio non standard e regolare l’ingrandimento fino a vederlo separato da 0, e questo avverrà sull’asse orizzontale, perché la parte iperreale è infinitesima di ordine inferiore rispetto alla parte iperimmaginaria. Ora 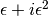$\epsilon + i\epsilon^2$ ci pare indistinto da $\epsilon$ perché l’ingrandimento non è sufficiente a individuare l’infinitesimo di ordine superiore, e lo stesso avviene applicando qualsiasi ulteriore microscopio standard. Con un secondo microscopio non standard, infine, sarà possibile accorgersi che la parte immaginaria non è nulla.

Un punto del piano ipercomplesso infinitamente vicino all’origine corrisponde a un numero infinitesimo. Per essere infinitesimo avrà quindi infinitesime sia la parte (iper)reale che quella (iper)immaginaria.

Complessi infiniti¶

Rappresentiamo nel piano ipercomplesso il punto 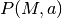$P(M, a)$ o il vettore 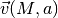$\vec v(M, a)$ , corrispondenti a 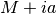$M + ia$ . Immaginiamo per semplicità che M e a siano positivi.

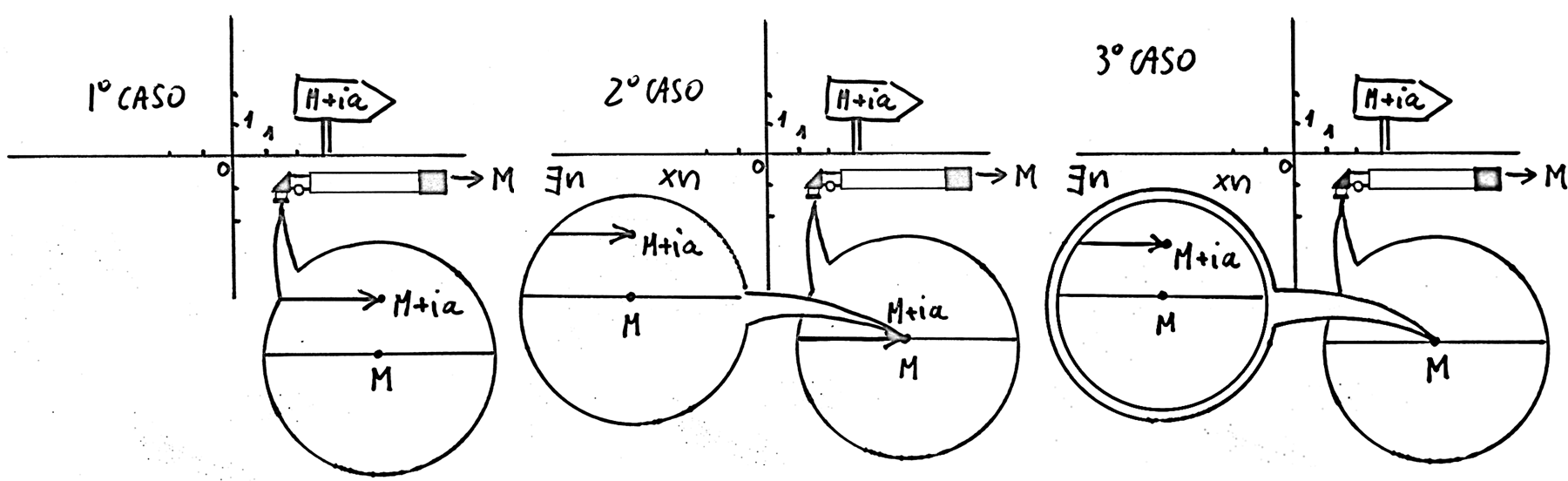
Per i nostri scopi lo zoom può risultare inadatto. Infatti la caratteristica dello zoom è di abbracciare nello stesso campo visivo l’origine e un numero lontano, anche infinitamente lontano. Riducendo la scala di visualizzazione in questo modo, però, si rischia di rendere indistinguibili eventuali infiniti di ordine inferiore.

Con un telescopio non standard centriamo il campo visivo su M. Si presentano tre possibilità:

I tre casi per un iperreale complesso infinito: $M + ia$ .

La visualizzazione è sufficiente: il telescopio, che mostra alla scala ordinaria la zona del piano ipercomplesso nei pressi di M, visualizza già la parte iperimmaginaria distinta da quella iperreale.
M + ia sembra coincidere con M: abbiamo bisogno di un microscopio standard per per distinguerli e individuare il punto.
M + ia non si vede, perché si vede solo M. Per farlo rientrare nel campo visivo occorrerà applicare uno zoom standard.

Un punto del piano ipercomplesso infinitamente lontano dall’origine corrisponde a un numero complesso infinito. Per essere infinito basta quindi che abbia infinita la parte reale o la parte immaginaria.

Per essere finito non infinitesimo, un numero ipercomplesso deve avere la parte reale e la parte immaginaria finite e almeno una delle due non infinitesima.

Il modulo e il tipo di ipercomplesso¶

Per classificare il tipo di complesso iperreale, è più facile riferirsi al suo modulo.

Un numero complesso è infinitesimo, infinito o finito non infinitesimo a seconda che sia di quel tipo il suo modulo.

Se il punto corrispondente è interno a ogni circonferenza di centro l’origine e di raggio standard, allora il numero complesso è infinitesimo.
Se il punto corrispondente è esterno a ogni circonferenza di centro l’origine e di raggio standard, allora il numero complesso è infinito.
Se il punto corrispondente giace fra due circonferenze di centro l’origine e raggi standard, allora il numero complesso è finito non infinitesimo.

Riassumendo¶

Come per i complessi nel piano cartesiano dei reali, così anche gli ipercomplessi si rappresentano nel piano degli iperreali. E quindi avremo ipercomplessi infinitesimi, finiti non infinitesimi o infiniti a seconda delle loro parti (iper)reali e (iper)immaginarie, o più semplicemente, del tipo del loro modulo. La rappresentazione dei punti che corrispondono a questi numeri si fa nei modi già visti, con microscopi, telescopi e zoom.

Esercizi¶

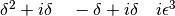
Visualizza nel piano ipercomplesso $\delta^2 + i\delta\ \ \ -\delta+i\delta\ \ \ i\epsilon^3$
Visualizza nel piano ipercomplesso $M - iM\ \ \ -\delta+iM\ \ \ iM^2\ \ \ a - iM\ \ \ M + i\delta$