Confronti fra iperreali¶

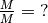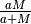Abbiamo visto che il rapporto fra due numeri di tipo I è una forma indeterminata. Il caso elementare è infatti $\frac{M}{M} = \mbox{?}$ e nulla si può dire di più, mancando ulteriori informazioni. Vediamo però un caso un po’ più impegnativo: $\frac{aM}{a+M}$ . Ricorrendo alle tavole del prodotto e della somma si sarebbe tentati di classificare questo rapporto secondo i tipi $\frac{I}{I}$ come il precedente. 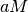Però il ragionamento intuitivo ci dice che il numero $a$ nel denominatore influisce sul risultato molto di meno rispetto al numeratore: in $aM$ il numero a viene moltiplicato infinite volte, mentre in 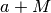$a+M$ , a si aggiunge all’infinito e rispetto ad esso è poco rilevante. 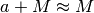Quindi $\ a+M \approx M\$ e il rapporto si può approssimativamente semplificare, determinando il tipo fni. Il ragionamento “a spanne” può essere formalizzato con una tecnica che tornerà utile: mettere in evidenza il termine più rilevante.

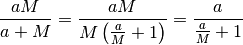
$\frac{aM}{a+M}=\frac{aM}{M\left(\frac{a}{M}+1\right)}= \frac{a}{\frac{a} M +1}$

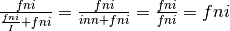
Da qui, l’analisi dei tipi: $\frac{fni}{\frac{fni}{I} + fni}= {\frac{fni}{inn+fni}}={\frac{fni}{fni}}=fni$

Confrontare due infinitesimi¶

Siamo abituati a confrontare le distanze stradali, l’altezza delle persone, il peso di due oggetti dots L’operazione che facciamo spontaneamente è valutare la differenza fra due misure e in genere ci sembra un’informazione sufficiente. Ma esaminiamo due casi:

Uno studente in sei mesi cresce di 10 cm, partendo da un’altezza di 160 cm.
Il Ponte di Brooklin, lungo circa 1800m, si allunga di più di un metro passando dall’inverno all’estate.

È banale dire che il ponte “cresce” di più, d’altra parte è anche molto più lungo. Se si valuta l’allungamento in rapporto alla misura iniziale, si vede che lo studente in sei mesi cresce in proporzione 112 volte più del ponte. Cioè se il ponte fosse ridotto ad un modellino di 160 cm, si allungherebbe di meno di 1 mm. Il segreto per valutare correttamente sta nel termine “in proporzione”: non si confrontano due misure con il calcolo della loro differenza, ma con il loro quoziente . Anche con due numeri di tipo inn useremo lo stesso procedimento: per confrontarli valuteremo il quoziente fra gli infinitesimi.

La tavola delle divisioni ci dice che il quoziente ${\epsilon \over \delta}$ è indeterminato, cioè ammette più risultati. Ma entriamo nei dettagli. D’ora in avanti, per semplificare, supporremo che i due infinitesimi siano quantità positive.

Gli infinitesimi sono dello stesso ordine.

Se usiamo due numeri standard, il rapporto 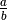${a\over b}$ esprime la misura di a secondo b, è di tipo fni , cioè è un numero che si colloca fra due numeri standard. Sappiamo già che se a, b sono molto piccoli troveremo un opportuno microscopio standard che li visualizza vicini e distinti. Ma in questo caso, trattandosi di infinitesimi, nessun microscopio standard riesce a visualizzarli distinti da zero. 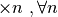Cioè per tutti gli n ingrandimenti possibili ( $\times n \ , \forall n$ ) i due infinitesimi e lo zero coincidono. Allora bisogna usare un microscopio non standard e puntarlo sullo zero. Avremo due casi:

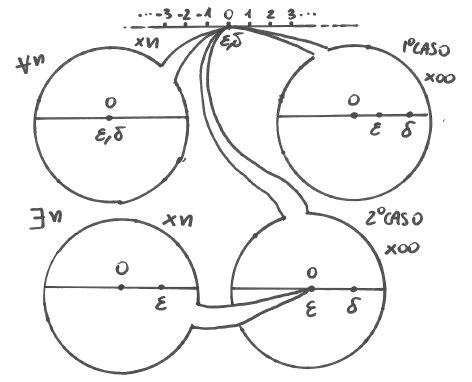
i due infinitesimi sono entrambi visibili nel campo visivo del microscopio, regolato allo stesso (infinito) ingrandimento: sono distinti sulla retta, vicini allo zero ma separati da esso (primo caso).
uno dei due infinitesimi è più piccolo dell’altro, ma non infinitamente più piccolo. Quindi uno si distingue da zero, ma non l’altro. Bisogna allora usare un secondo microscopio, questa volta un microscopio standard, e puntarlo sullo zero nel campo visivo del primo microscopio. Esisterà un opportuno ingrandimento finito ( 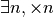$\exists n, \times n$ ) che consente di separare dallo zero anche il secondo infinitesimo (secondo caso).

Se per entrare nel mondo infinitamente piccolo dei 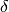$\delta$ e degli $\epsilon$ facciamo uso di un solo microscopio non standard e con questo riusciamo a distinguerli fra loro e dallo zero allora si dice che i due infinitesimi sono del primo ordine. L’ordine di un infinitesimo corrisponde al numero di microscopi non standard utilizzati in sequenza per distinguerlo dallo zero. Quindi se basta un solo microscopio non standard per visualizzarli distinti, due infinitesimi sono entrambi del primo ordine, non importa se abbiamo avuto bisogno anche di un microscopio standard.

In generale, se due infinitesimi sono dello stesso ordine, si distinguono entrambi da zero e fra loro grazie allo stesso numero di microscopi non standard.

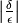Il rapporto ${\left|\epsilon \over \delta\right|}$ (oppure ${\left|\delta \over \epsilon\right|}$ ) calcola quante volte il secondo infinitesimo sta nel primo. Nel campo visivo del microscopio non standard il numero di volte può essere contato, quindi il risultato è un fni. Sappiamo che un fni si colloca fra due numeri standard, quindi 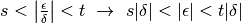$s<{\left|\epsilon \over \delta\right|}<t\ \rightarrow \ s|\delta|<|\epsilon|<t|\delta|$ . 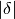Stiamo esprimendo la misura di $|\epsilon|$ in unità $|\delta|$ . Insomma, seppur ridotti al mondo infinitamente microscopico, possiamo simulare le stesse operazioni di confronto imparate con i segmenti e i numeri standard.

Il primo infinitesimo è di ordine superiore: $\epsilon=o(\delta)$ .

Il secondo caso è quello in cui fra i due infinitesimi, il primo è “più infinitesimo” del secondo. Seguendo il metodo del caso precedente, applicare qualsiasi microscopio standard allo zero risulta inutile. Applichiamo dunque un microscopio non standard e regoliamo l’ingrandimento fino al valore infinito che ci consente di visualizzare l’infinitesimo maggiore (diciamo 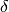$\delta$ ), che è il numero iperreale meno piccolo. 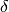$\delta$ appare per primo nel campo visivo mentre $\epsilon$ è troppo infinitamente vicino allo zero, troppo piccolo per poter essere visualizzato con quell’ingrandimento. Non lo potremo visualizzare nemmeno aiutandoci con un altro microscopio che sia standard: questa volta anche il secondo microscopio deve essere non standard. 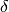Quando nel campo visivo $\epsilon$ comincia a distinguersi dallo zero (siamo a infiniti di infiniti ingrandimenti), $\delta$ non si vede più. 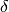Per poter vedere $\epsilon$ abbiamo raggiunto un ingrandimento così infinitamente forte che $\delta$ è uscito dal campo visivo. 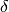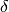Il segmento di misura $\delta$ si è infinitamente allungato: grazie al secondo ingrandimento, $\delta$ da infinitesimo è diventato un infinito. Se lo volessimo rivedere dovremmo cercare di attenuare l’ingrandimento e applicare un telescopio (oppure uno zoom) non standard. In una situazione così, si dice che $\epsilon$ è infinitesimo di ordine superiore rispetto a 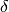$\delta$ (cioè è infinitamente più piccolo) e si scrive 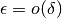$\epsilon=o(\delta)$ . Il rapporto fra i due risulta quindi un numero infinitesimo non nullo quindi il secondo infinitesimo è di ordine superiore.

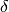Il terzo caso è quello in cui fra i due infinitesimi, il primo è “meno infinitesimo” del secondo. In pratica nella scala in cui si visualizza il denominatore, il numeratore si trova a distanza infinita. Quindi $\epsilon$ è infinitesimo di ordine inferiore ( $\delta$ è infinitesimo di ordine superiore), quindi stavolta 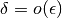$\delta=o(\epsilon)$ . Il rapporto fra i due risulta quindi un numero infinito quindi il secondo infinitesimo è di ordine inferiore.

Confrontare due infiniti¶

Il tipo 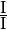$\frac{\mbox{I}}{\mbox{I}}$ è indefinito: può dare origine a un fni, a un I oppure a un inn. Trattandosi di infiniti e non di infinitesimi, useremo gli zoom invece dei microscopi e seguiremo un percorso simile. Anche qui immaginiamo per semplicità che M e N siano infiniti positivi.

Infiniti dello stesso ordine¶

I due infiniti non sono “a tiro” per uno zoom standard. Occorre usare uno zoom non standard perché si trovano all’infinito. Regolando l’ingrandimento di uno zoom non standard, se $M > N$ il numero M sarà il primo a comparire nel campo visivo, distinto da zero. Di nuovo si avranno due casi: che anche il punto N risulti separato dall’origine, oppure che occorra usare un microscopio standard per separarlo. In ogni caso il rapporto fra i due infiniti è calcolabile nel campo visivo dello zoom, eventualmente tenendo conto degli ingrandimenti del microscopio. Poiché usiamo un solo zoom non standard, diciamo che entrambi i numeri sono infiniti di ordine 1. 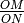Il rapporto fra i due segmenti infiniti $\frac{OM}{ON}$ (e anche il suo reciproco) risulterà un numero di tipo fni. Il numero di zoom non standard necessari a visualizzare un iperreale infinito dipende dal suo ordine di infinito. Se M e N sono infiniti dello stesso ordine, il numero di zoom non standard che usiamo per visualizzarli è lo stesso. Infatti possiamo averli nello stesso campo visivo.

Infiniti di ordine diverso¶

Se $M > N$ , questa volta N è il primo numero a comparire separato da zero nel campo visivo di uno zoom non standard. Ma M in questa situazione si trova all’infinito, cioè non è raggiungibile mediante uno zoom standard puntato su N. Occorre usare un secondo zoom non standard e a quel grado di infinito (infinito di infinito) N è schiacciato sullo zero. Nessun microscopio standard può distinguere N da zero. Si può farlo solo puntando sullo zero un microscopio non standard nel campo visivo dello zoom non standard, in modo da ridurre il grado di infiniti ingrandimenti. Possiamo dire che M è un infinito di secondo ordine, mentre N lo è di primo. Siccome nel visualizzare N, M è andato all’infinito, occorrono infiniti segmenti ON per misurare OM. Quindi il quoziente fra i numeri M e N dà luogo a un numero infinito. Questo succede in generale, cioè se M è un infinito di ordine superiore a N.

Se M è un infinito di ordine inferiore, il rapporto fra M e N risulta infinitesimo.

Riassumendo¶

Il confronto fra due numeri è utile se risulta dal loro rapporto, non dalla loro differenza. Il rapporto fra due infinitesimi è indefinito. Visualizzandoli con i microscopi non standard si distinguono 3 casi: possono essere infinitesimi dello stesso ordine, oppure il primo, o il secondo, può essere di ordine superiore. Le tre situazioni portano a risultati diversi. Lo stesso accade nel rapporto fra infiniti. Questa volta invece dei microscopi, si usano gli zoom non standard.

tipo	confronto
i	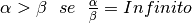$\alpha > \beta \ \ se \ \ \frac{\alpha}{\beta} = I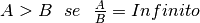nfinito$
I	$A > B \ \ se \ \ \frac{A}{B} = Infinito$

Esercizi¶

Il primo esempio del capitolo ricorda la formula della resistenza equivalente nel caso di un circuito elettrico con due resistenze in parallelo. Segui l’analisi dei tipi sviluppata nel testo e applicala al circuito in questione.
Di che tipo è l’espressione: 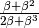$\quad {{\beta+\beta^2}\over{2\beta+\beta^3}}\$ ? (Se segui la tecnica spiegata all’inizio del capitolo, vedrai che il tipo risultante non è i).
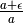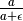Di quali e quanti strumenti hai bisogno per visualizzare il numero che risulta da $\frac{a+\epsilon}{a}$ ? E da $\frac{a}{a+\epsilon}$ ?
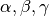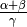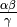Se $\alpha ,\beta ,\gamma$ sono infinitesimi dello stesso ordine, come disponi gli strumenti per distinguere $\frac{\alpha + \beta} {\gamma}$ , ${\alpha \beta}\over{\gamma}$ ? E quali sono i tipi che che risultano?
Risolvi i due esercizi precedenti sostituendo i numeri infinitesimi con numeri infiniti.