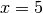Altri problemi introduttivi¶
Area di un triangolo parabolico¶
Consideriamo la regione di piano compresa tra la parabola di equazione:
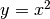 l’asse delle ascisse e una retta parallela all’asse delle ordinate, ad es.:
l’asse delle ascisse e una retta parallela all’asse delle ordinate, ad es.:
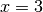 .
Chiamiamo triangolo parabolico questa regione e ci poniamo il problema di
calcolarne l’area.
.
Chiamiamo triangolo parabolico questa regione e ci poniamo il problema di
calcolarne l’area.
Possiamo osservare che per
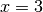 l’ordinata della parabola vale
l’ordinata della parabola vale
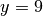 quindi il triangolo parabolico è contenuto nel rettangolo di base
quindi il triangolo parabolico è contenuto nel rettangolo di base
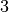 e altezza
e altezza
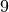 .
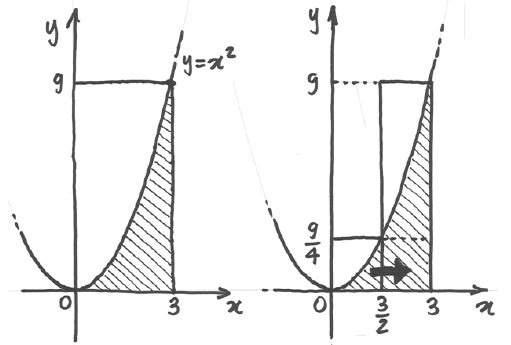
Quindi possiamo effettuare una prima stima molto grossolana dell’area
affermando
che deve essere minore di
.
Quindi possiamo effettuare una prima stima molto grossolana dell’area
affermando
che deve essere minore di
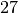 .
.
Possiamo ridurre l’incertezza dividendo l’intervallo
![[0; 3]](../../../_images/math/62313e8094924cbffbb426a032d992c721102a6e.png) in due parti uguali:
in due parti uguali:
![[0; \frac{3}{2}]](../../../_images/math/7488f3ee2c6b0da6380027916fb4e9caf2e7d31e.png) e
e
![[\frac{3}{2}; 3]](../../../_images/math/0e7b450ebf6c80c3ae1c3fa3887a038d49097929.png) .
Di sicuro l’area del triangolo parabolico sarà inferiore alla somma di due
rettangoli aventi base
.
Di sicuro l’area del triangolo parabolico sarà inferiore alla somma di due
rettangoli aventi base
 e altezze rispettivamente
e altezze rispettivamente
 e
e
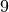 .
Quindi l’area cercata è minore di:
.
Quindi l’area cercata è minore di:
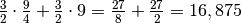
Se togliamo il secondo rettangolo e facciamo scorrere a destra il primo,
possiamo vedere che è contenuto nel triangolo parabolico,
quindi l’area cercata è maggiore di
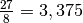 .
.
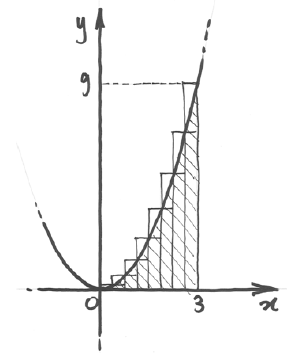
Si può migliorare la stima dividendo l’intervallo in
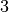 parti, e poi in
parti, e poi in
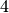 ,
, 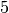 e così via.
Maggiore è il numero di suddivisioni, minore sarà l’incertezza.
Se riuscissimo a dividere l’intervallo in infinite parti l’errore
sarebbe infinitesimo.
e così via.
Maggiore è il numero di suddivisioni, minore sarà l’incertezza.
Se riuscissimo a dividere l’intervallo in infinite parti l’errore
sarebbe infinitesimo.
Ma proviamo a ricavare una formula generale nel caso della suddivisione in
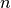 parti.
In questo caso gli estremi destri di ogni suddivisione hanno ascissa
parti.
In questo caso gli estremi destri di ogni suddivisione hanno ascissa
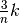 ,
con
,
con
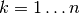 .
Le altezze dei rettangoli, che sono le ordinate di k in quei punti valgono
.
Le altezze dei rettangoli, che sono le ordinate di k in quei punti valgono
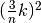 e l’area del k-mo rettangolo vale:
e l’area del k-mo rettangolo vale:
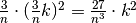 La somma di tutte queste aree sarà:
La somma di tutte queste aree sarà:
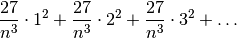
E raccogliendo
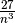 si ottiene:
si ottiene:
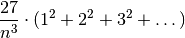
Da altri studi, i matematici hanno trovato che la somma dei quadrati dal numero 1 al numero n è data dalla formula:
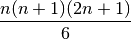
Ad esempio per
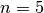 abbiamo che
abbiamo che
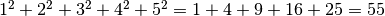 e
e
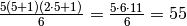
La somma delle aree degli n rettangoli può allora essere scritta nella forma:
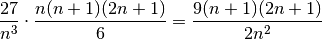
Se consideriamo un numero
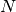 infinito di rettangoli possiamo osservare che
infinito di rettangoli possiamo osservare che
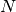 e
e
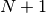 saranno infinitamente vicini e questo varrà anche per
saranno infinitamente vicini e questo varrà anche per
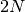 e
e
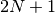
Quindi la formula precedente è equivalente a:
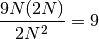
possiamo concludere che la somma delle aree degli infiniti rettangoli è
infinitamente vicina a
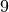 che è l’area del triangolo parabolico.
che è l’area del triangolo parabolico.
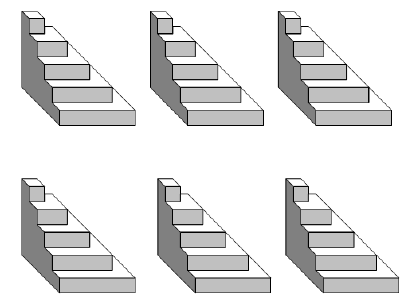
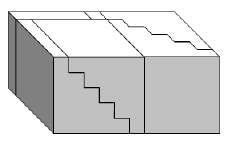
Dimostrazione visiva della formula per la somma dei primi n quadrati¶
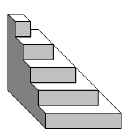
Possiamo rappresentare i numeri con dei cubetti. In questo caso i numeri quadrati saranno rappresentati da prismi a base quadrata di altezza unitaria. La somma di quadrati può essere rappresentata da una piramide a gradoni realizzata sovrapponendo questi prismi.
Consideriamo
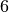 di queste piramidi.
di queste piramidi.
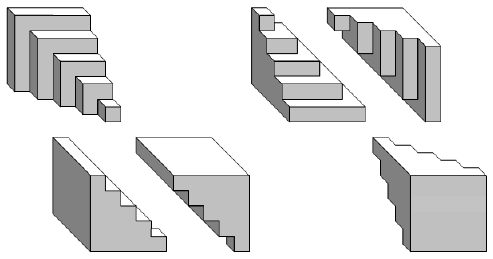
Ora possiamo ruotare le piramidi...
...iniziamo a incastrare due coppie di “piramidi”...
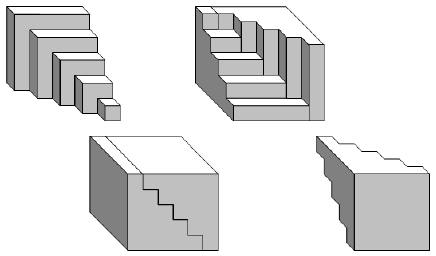
...incastriamo anche la terza piramide ottenendo due parallelepipedi...
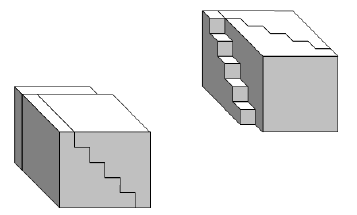
...accostiamo i due parallelepipedi in modo da ottenerne uno unico...
Abbiamo dimostrato così che sei “piramidi” sono equivalenti a un parallelepipedo.
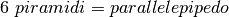
Ma il volume di una piramide è dato dalla somma di enne quadrati:
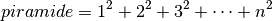
E il volume del parallelepipedo è:
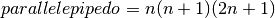
Da cui si ricava:
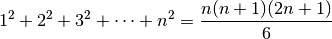
Riassumendo¶
I numeri Iperreali permettono di affrontare in modo nuovo alcuni problemi, ma finora li abbiamo usati in modo piuttosto intuitivo. Ora dobbiamo definire in modo molto preciso cosa intendiamo con “infinitesimo”, “infinito” e “numero iperreale”.
Una definizione ben fondata di questi termini ci permetterà di usarli al pari di tutti gli altri oggetti matematici.
Esercizi¶
- Calcola l’area del triangolo parabolico delimitato dalla parabola
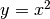 ,
dall’asse delle ascisse e dalla retta
,
dall’asse delle ascisse e dalla retta
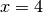
- Calcola l’area del triangolo parabolico delimitato dalla parabola
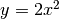 ,
dall’asse delle ascisse e dalla retta
,
dall’asse delle ascisse e dalla retta
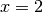
- Calcola l’area del segmento parabolico delimitato dalla parabola
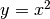 ,
e dal segmento che congiunge il vertice con il suo punto di ascissa
,
e dal segmento che congiunge il vertice con il suo punto di ascissa
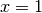
- Calcola l’area del segmento parabolico delimitato dalla parabola
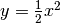 ,
e dal segmento che congiunge il vertice con il suo punto di ascissa
,
e dal segmento che congiunge il vertice con il suo punto di ascissa