Funzioni iperreali¶
Per i nostri scopi, solo in questo capitolo, indichiamo con 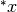 un
numero qualsiasi iperreale (x star), per distinguerlo da un qualsiasi x
reale.
un
numero qualsiasi iperreale (x star), per distinguerlo da un qualsiasi x
reale.
Finora abbiamo utilizzato gli iperreali nei calcoli più comuni, per capirne le proprietà. Li abbiamo inseriti in addizioni e sottrazioni, moltiplicazioni e divisioni, potenze, radici quadrate... Abbiamo usato le funzioni algebriche: intere, razionali e irrazionali. In questo capitolo l’uso degli iperreali viene esteso alle funzioni in genere, a quelle già incontrate e alle altre, trascendenti.
Estendere il dominio¶
Il dominio di una funzione è l’insieme dei numeri che la funzione
utilizza per produrre i suoi risultati.
Non è difficile estendere un dominio dai reali agli iperreali. Per es. un
dominio così definito:
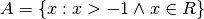 , l’estensione iperreale è:
, l’estensione iperreale è:
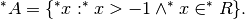 In questo modo l’insieme A è stato arricchito degli infiniti (in questo
caso si tratta degli infiniti positivi), degli infinitesimi e di tutti
gli iperreali contenuti nelle monadi di A.
Si dice che
In questo modo l’insieme A è stato arricchito degli infiniti (in questo
caso si tratta degli infiniti positivi), degli infinitesimi e di tutti
gli iperreali contenuti nelle monadi di A.
Si dice che 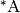 (A star) è l’estensione iperreale di A.
(A star) è l’estensione iperreale di A.
Un altro esempio: l’estensione iperreale dell’intervallo chiuso [ 1 , 3 ] è
l’intervallo iperreale ![^*[ 1 , 3 ]](../../../_images/math/bbff4c18db99b50bdacefab161b7dbc0d2b903d1.png) , cioè l’insieme dei numeri iperreali
, cioè l’insieme dei numeri iperreali
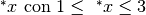 .
.
L’estensione di un insieme di reali è l’insieme di iperreali che verificano le stesse proprietà.
Estendere la funzione¶
Se una funzione opera su un insieme di reali (funzione reale di variabile reale) come si comporterà dopo l’estensione iperreale del suo dominio? Noi vorremmo mantenere le sue proprietà, in modo da poter risolvere problemi come quelli dei capitoli introduttivi senza complicazioni ulteriori.
Ci sono casi facili.
La funzione 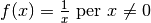 è definita su tutti i
reali tranne zero. L’estensione del dominio non comporta problemi
ed è facile calcolarla anche con gli iperreali:
è definita su tutti i
reali tranne zero. L’estensione del dominio non comporta problemi
ed è facile calcolarla anche con gli iperreali:
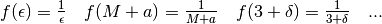 Per altre funzioni l’estensione non è così elementare: per esempio
che risultato dà
Per altre funzioni l’estensione non è così elementare: per esempio
che risultato dà 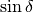 ? E varrà ancora che
? E varrà ancora che
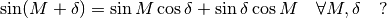 Oppure che:
Oppure che:
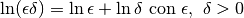 ?
?
Sarebbero tutte proprietà da ridefinire. Per non doverlo fare
ad ogni estensione, assumiamo che di ogni funzione
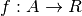 esiste l’estensione iperreale
esiste l’estensione iperreale
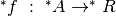 , dove
, dove
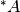 è l’estensione iperreale di A e
è l’estensione iperreale di A e
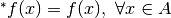 .
.
Questo non implica il contrario: mentre esiste l’estensione iperreale
di ogni funzione standard f(x), non è detto che ogni funzione
iperreale sia il risultato di un’estensione iperreale.
Per es. la funzione iperreale “parte standard di x” (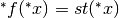 )
non ha una funzione corrispondente nei reali.
Infatti non esiste la parte standard di un numero reale. Il dominio della
funzione “parte standard di x” è la galassia principale, che
non è l’estensione iperreale dell’insieme R (R ha come estensione
)
non ha una funzione corrispondente nei reali.
Infatti non esiste la parte standard di un numero reale. Il dominio della
funzione “parte standard di x” è la galassia principale, che
non è l’estensione iperreale dell’insieme R (R ha come estensione 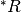 ).
La funzione “parte standard” associa ad un numero finito la sua parte
non infinitesima:
).
La funzione “parte standard” associa ad un numero finito la sua parte
non infinitesima: 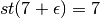 .
Il grafico alla scala ordinaria di questa funzione sembra la retta
bisettrice del primo e terzo quadrante, ma è fatto da una successione
infinita di tratti orizzontali infinitesimi, perché la funzione è costante
su ogni monade.
.
Il grafico alla scala ordinaria di questa funzione sembra la retta
bisettrice del primo e terzo quadrante, ma è fatto da una successione
infinita di tratti orizzontali infinitesimi, perché la funzione è costante
su ogni monade.
E osserviamo inoltre che nel campo visivo di uno zoom non standard il grafico manca: la parte standard di un infinito non esiste.
Se potessimo ignorare l’esistenza degli infinitesimi, allora la parte
standard si comporterebbe come la funzione identica, perché st(7) = 7.
Ma in generale la funzione identica è diversa: nei reali associa a ogni numero
se stesso,
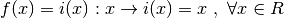 .
Nel piano cartesiano i valori di i(x) si valutano sull’asse Y, quindi
y = x, cioè la ben nota retta bisettrice.
.
Nel piano cartesiano i valori di i(x) si valutano sull’asse Y, quindi
y = x, cioè la ben nota retta bisettrice.
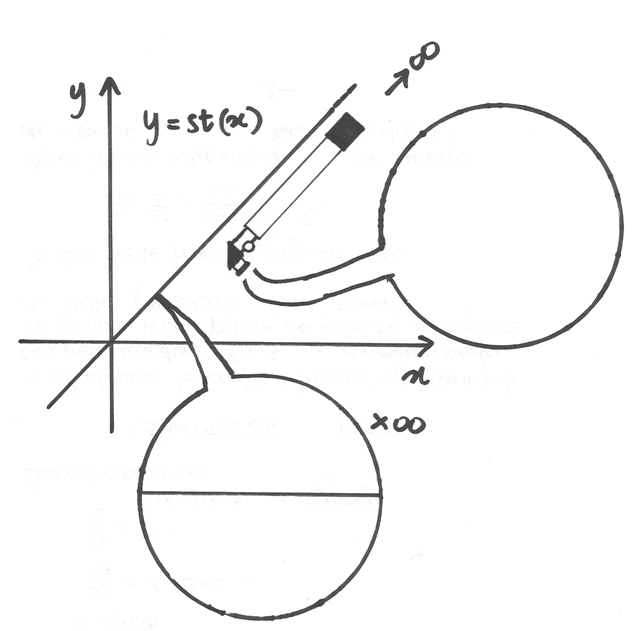
Negli iperreali la funzione identica dà per esempio
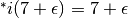 . L’estensione iperreale di y = i(x) è
l’identità iperreale
. L’estensione iperreale di y = i(x) è
l’identità iperreale
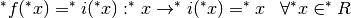 che associa ad
ogni iperreale se stesso. Il grafico di tale funzione è quello di fig.2: in
qualsiasi scala (nella scala ordinaria, a infiniti ingrandimenti e anche a
distanza infinita) è la bisettrice del primo-terzo quadrante, come nel caso
corrispondente reale.
che associa ad
ogni iperreale se stesso. Il grafico di tale funzione è quello di fig.2: in
qualsiasi scala (nella scala ordinaria, a infiniti ingrandimenti e anche a
distanza infinita) è la bisettrice del primo-terzo quadrante, come nel caso
corrispondente reale.
I sottoinsiemi di *R¶
- L’estensione iperreale dei naturali N è l’insieme degli ipernaturali *N.
- L’estensione iperreale degli interi Z sarà l’insieme degli iperinteri *Z.
- Analogamente si costruisce l’estensione *Q dei numeri iperrazionali, espressi dal rapporto fra due iperinteri.
Sui grafici¶
Quando mettiamo in grafico una funzione iperreale ci serviamo del piano dei numeri iperreali. Questo vuol dire che usiamo rette iperreali sia per l’ascissa che per l’ordinata. Quindi il piano iperreale è formato dai punti che sono in corrispondenza biunivoca con le coppie ordinate di numeri iperreali.
Riassumendo¶
Per risolvere i problemi presentati all’inizio del libro, si immagina che ogni funzione reale conosciuta abbia una corrispondente estensione iperreale, calcolata su un insieme che è anch’esso estensione iperreale del dominio della funzione originaria. Le funzioni così estese hanno le stesse proprietà delle loro corrispondenti reali. Esistono poi altre funzioni iperreali, come la funzione standard, che non sono estensione di una funzione reale. Si discute della diversità fra la funzione parte standard e la funzione identica. I grafici di tali funzioni si tracciano nel piano iperreale.
.png)