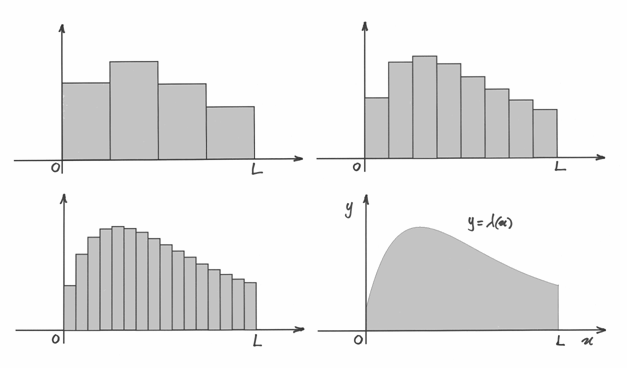
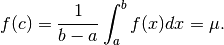Il valore medio e il baricentro¶
La media delle funzioni¶
Tutti sappiamo cos’è la media di alcuni numeri: è il valore che tutti i numeri
avrebbero uguale, se volessimo ottenere la stessa somma. Per esempio la media
fra 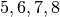 è
è 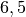 non perché sia il valore intermedio, ma perchè
i numeri dati sommano
non perché sia il valore intermedio, ma perchè
i numeri dati sommano 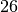 , e se ognuno di quei numeri fosse
, e se ognuno di quei numeri fosse 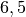 otterremmo la stessa somma.
otterremmo la stessa somma.
Il concetto di media sottintende quindi un procedimento di somma e di successiva divisione per il numero di valori da mediare. Questo ci porta a utilizzare le tecniche di calcolo apprese fino qui.
La media degli 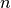 valori di una successione
valori di una successione 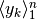 sarà
sarà 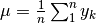 e
e 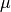 è detto valore medio della
successione. Notare che se l’indice
è detto valore medio della
successione. Notare che se l’indice  varia fra
varia fra 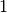 e
e 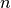 si
contano
si
contano 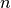 termini, cioè
termini, cioè 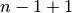 . Supponiamo che la successione
precedente sia ricavata a partire dal tredicesimo termine di un’altra
successione
. Supponiamo che la successione
precedente sia ricavata a partire dal tredicesimo termine di un’altra
successione 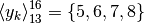 .
Il valor medio non cambia, i termini sono sempre 4, cioè
.
Il valor medio non cambia, i termini sono sempre 4, cioè 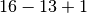 . Quindi
se la successione è genericamente
. Quindi
se la successione è genericamente 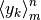 ,
allora la formula del valor medio diventa
,
allora la formula del valor medio diventa
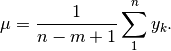
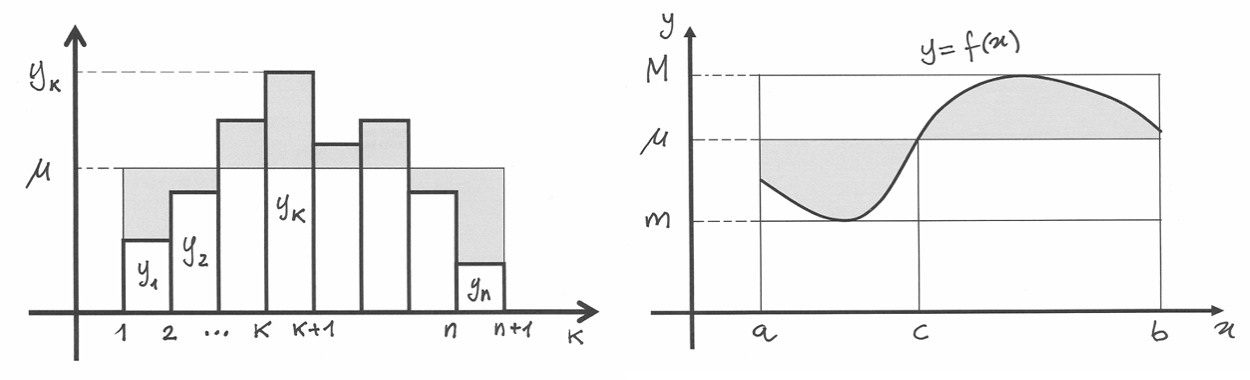
Nel caso di una funzione a dominio discreto 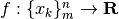 ,
con
,
con 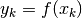 , la formula precedente va adattata.
Fra due
, la formula precedente va adattata.
Fra due 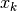 consecutivi la differenza in genere non è
consecutivi la differenza in genere non è 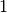 ,
come accade per gli indici. I punti del grafico hanno distanze orizzontali
,
come accade per gli indici. I punti del grafico hanno distanze orizzontali
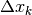 in genere diverse, da sommare nel denominatore della
formula, che diventa
in genere diverse, da sommare nel denominatore della
formula, che diventa 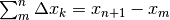 . Per la somma
al numeratore, poiché i punti non sono equidistanziati come in una successione,
bisogna considerare che ogni
. Per la somma
al numeratore, poiché i punti non sono equidistanziati come in una successione,
bisogna considerare che ogni 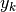 che si aggiunge pesa nella somma di più
o di meno, anche in relazione all’intervallo
che si aggiunge pesa nella somma di più
o di meno, anche in relazione all’intervallo 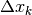 che lo distanzia
dal valore successivo. Per questo abbiamo:
che lo distanzia
dal valore successivo. Per questo abbiamo:
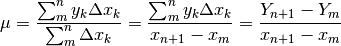
dove abbiamo fatto uso anche del teorema fondamentale del calcolo delle somme.
Si tratta di una media pesata: ogni 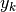 pesa
sulla somma tante volte quante sono indicate da
pesa
sulla somma tante volte quante sono indicate da 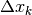 . Per fare
un esempio semplice, cerchiamo la media di:
. Per fare
un esempio semplice, cerchiamo la media di: 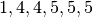
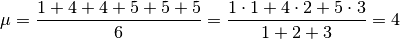
cioè il calcolo viene organizzato moltiplicando ogni valore per la frequenza
(=il numero di volte) con cui compare.
Un altro esempio per questa formula viene dalla cinematica. In questo caso  è la velocità media, cioè il rapporto fra lo spazio percorso
è la velocità media, cioè il rapporto fra lo spazio percorso 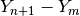 e l’intervallo di tempo
e l’intervallo di tempo 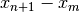 . Lo spazio, poi, è calcolabile come
differenza fra le due posizioni iniziale e finale, ma è anche
. Lo spazio, poi, è calcolabile come
differenza fra le due posizioni iniziale e finale, ma è anche
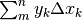 , la somma dei vari tratti che si ottengono
moltiplicando la velocità per la durata, in ogni tratto.
, la somma dei vari tratti che si ottengono
moltiplicando la velocità per la durata, in ogni tratto.
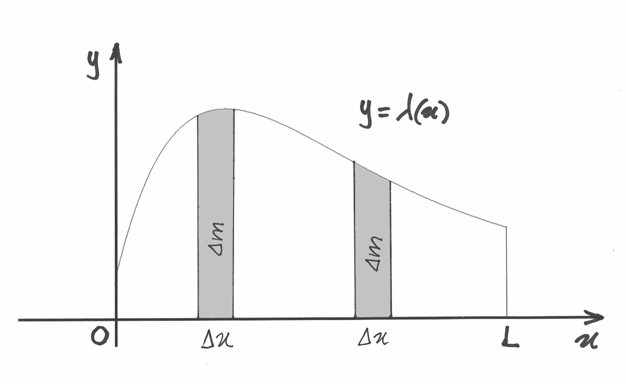
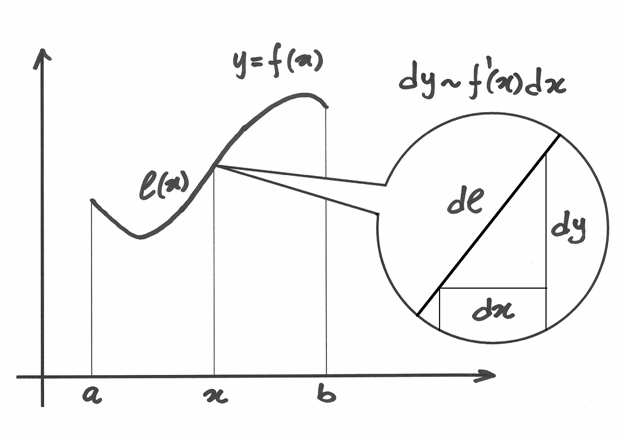
Consideriamo ora il caso di una funzione continua ![f:[a,b]\to \mathbf{R}](../../../_images/math/86bbcc1e6fd1ad5fca5cf93f9037be22a7432370.png) e cerchiamo il suo valore medio. Possiamo figurarci che
e cerchiamo il suo valore medio. Possiamo figurarci che 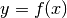 rappresenti
la velocità all’istante
rappresenti
la velocità all’istante  di un punto che si muove su una retta.
Se dividiamo l’intervallo dei tempi mediante infiniti punti in modo da avere
di un punto che si muove su una retta.
Se dividiamo l’intervallo dei tempi mediante infiniti punti in modo da avere
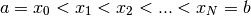
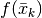 sarà la velocità nel k_esimo intervallo infinitesimo di tempo.
La media pesata delle velocità è
sarà la velocità nel k_esimo intervallo infinitesimo di tempo.
La media pesata delle velocità è
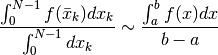
e quindi il valore medio della funzione è
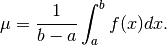
che corrisponde, secondo il teorema fondamentale del calcolo integrale, a
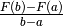 , dove
, dove 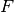 è una qualsiasi primitiva.
Nel parallelo cinematico,
è una qualsiasi primitiva.
Nel parallelo cinematico, 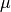 è la velocità media.
è la velocità media.
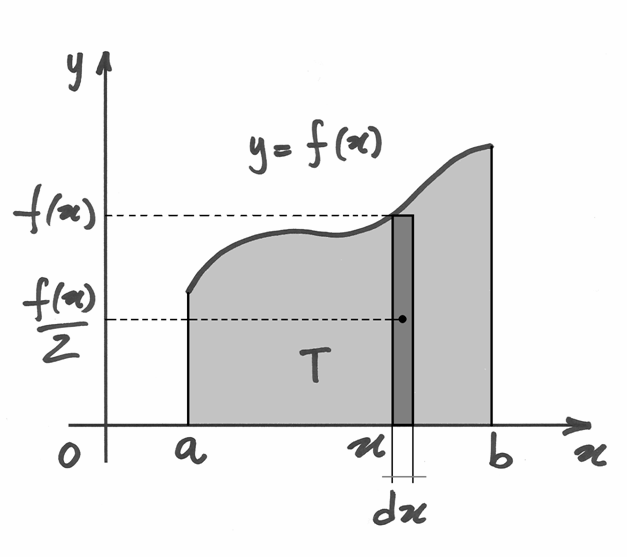
Ma esiste un altro parallelo interessante, quello geometrico. Poiché l’integrale
rappresenta l’area (con il suo segno) sottesa alla curva e 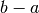 è
la misura della base di questa regione, allora
è
la misura della base di questa regione, allora 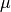 è l’altezza media,
necessaria ad un rettangolo per essere equiesteso (considerando aree positive
e negative). Lo stesso ragionamento si può fare per le funzioni a dominio discreto.
è l’altezza media,
necessaria ad un rettangolo per essere equiesteso (considerando aree positive
e negative). Lo stesso ragionamento si può fare per le funzioni a dominio discreto.
Qualche esempio¶
- Calcola il valore medio di
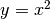 nell’intervallo
nell’intervallo ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) .
.
La soluzione:
![\mu=\frac{1}{1-0}\int_0^1x^2dx=\left[\frac{x^3}{3} \right]_0^1=\frac{1}{3}.](../../../_images/math/5fb56affb92164239effdfa08d639d34b46937fe.png)
Quindi, se tagliamo il grafico della funzione con un segmento orizzontale
all’altezza 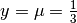 nell’intervallo dato , isoliamo un
rettangolo equiesteso alla figura curvilinea limitata dal grafico.
nell’intervallo dato , isoliamo un
rettangolo equiesteso alla figura curvilinea limitata dal grafico.
- Calcola il valore medio di
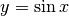 nell’intervallo
nell’intervallo ![[0,\pi]](../../../_images/math/1b989a72aeaf778381894e0025fe309783e17235.png) .
.
La soluzione:
![\mu=\frac{1}{\pi-0}\int_0^\pi\sin xdx=\frac{1}{\pi}\left[-\cos x\right]_0^\pi=
\frac{-\cos\pi+\cos 0}{\pi}=\frac{2}{\pi}=0,637.](../../../_images/math/040ff3f39d89a15f5e7abac4877ae88944739f46.png)
In ogni disegno della figura precedente, le parti grigie riempiono in vario modo zone equiestese.
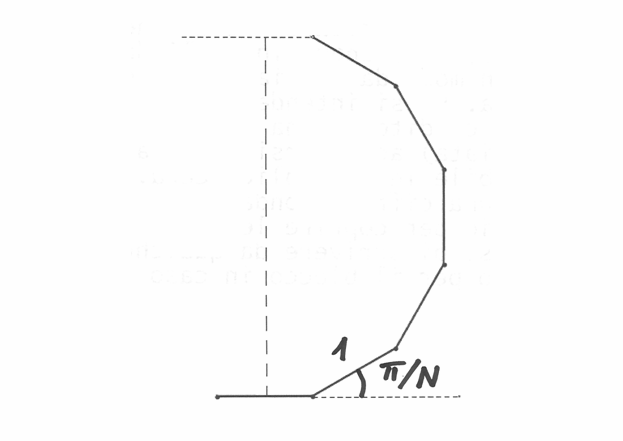
L’asta rotante¶
C’è una rappresentazione meccanica per l’ultimo risultato. Si immagina un’asta
di lunghezza unitaria che ruota attorno al proprio asse nel piano del foglio.
Il movimento avviene a scatti di ampiezza 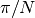 , con
, con 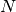 ipernaturale infinito.
ipernaturale infinito.
Dopo 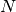 scatti l’asta ha ruotato di un angolo piatto e un osservatore
posto sul piano di rotazione ha visto crescere ad ogni scatto la lunghezza
apparente dell’asta, fino alla sua misura reale, corrispondente ad una rotazione
di
scatti l’asta ha ruotato di un angolo piatto e un osservatore
posto sul piano di rotazione ha visto crescere ad ogni scatto la lunghezza
apparente dell’asta, fino alla sua misura reale, corrispondente ad una rotazione
di 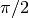 , per poi decrescere. La somma delle lunghezze apparenti è
il diametro del poligono regolare di cui l’asta ha disegnato il semiperimetro.
L’integrale del secondo esempio misura il diametro della figura e il risultato,
diviso per il numero di scatti compiuti dal movimento, rappresenta la lunghezza
media apparente dell’asta. Approssimiamo il poligono con una circonferenza di
lunghezza
, per poi decrescere. La somma delle lunghezze apparenti è
il diametro del poligono regolare di cui l’asta ha disegnato il semiperimetro.
L’integrale del secondo esempio misura il diametro della figura e il risultato,
diviso per il numero di scatti compiuti dal movimento, rappresenta la lunghezza
media apparente dell’asta. Approssimiamo il poligono con una circonferenza di
lunghezza 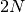 , così otteniamo che il diametro è lungo
, così otteniamo che il diametro è lungo 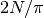 e quindi l’asta appare lunga in media
e quindi l’asta appare lunga in media 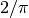 .
.
La media e le funzioni¶
La media di una funzione a dominio discreto può benissimo essere diversa da ogni valore che la funzione assume nell’intervallo.
Ma questo non può avvenire per una funzione continua: almeno uno dei suoi valori è uguale al valore medio.
Negli esempi precedenti è facile individuare questi casi. 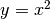 raggiunge
il valore medio, relativamente all’intervallo
raggiunge
il valore medio, relativamente all’intervallo ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) , per
, per
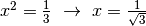 .
.
Invece 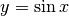 nell’intervallo
nell’intervallo ![[0,\pi]](../../../_images/math/1b989a72aeaf778381894e0025fe309783e17235.png) assume il valor medio in
due casi:
assume il valor medio in
due casi: 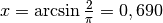 e
e
 , per cui l’asta per due volte appare
lunga quanto la sua lunghezza media apparente.
, per cui l’asta per due volte appare
lunga quanto la sua lunghezza media apparente.
Il fatto che questo sia vero per tutte le funzioni continue può essere dimostrato.
Infatti una funzione ![f:[a,b]\to\mathbf{R}](../../../_images/math/a11f00b9981d6439a5bcdf02e4e93ab8df515488.png) , se è continua ammette un
minimo assoluto (
, se è continua ammette un
minimo assoluto (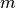 ) e un massimo assoluto (
) e un massimo assoluto (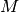 ) e assume
ogni valore fra i due. La conseguenza è
) e assume
ogni valore fra i due. La conseguenza è
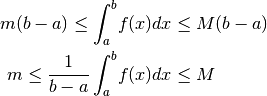
quindi esiste un punto 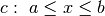 tale che
tale che
In relazione al concetto di media, la differenza fra le funzioni a dominio discreto e le funzioni continue è che entrambi i tipi di funzioni hanno un valore medio compreso fra il minimo e il massimo della funzione nell’intervallo dato, ma solo le funzioni continue assumono questo valore almeno una volta.
La dispersione e la deviazione standard¶
Una coppia di quarantenni ha la stessa età media che c’è fra un bimbo di due anni
e un nonno di 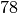 . La differenza fra i due gruppi è la dispersione dei valori
che danno luogo allo stesso valore medio. Le considerazioni che seguono riguardano
appunto il concetto di dispersione.
. La differenza fra i due gruppi è la dispersione dei valori
che danno luogo allo stesso valore medio. Le considerazioni che seguono riguardano
appunto il concetto di dispersione.
Data una successione di valori 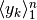 che ha media
che ha media 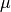 ,
ogni valore ha una differenza rispetto alla media data da
,
ogni valore ha una differenza rispetto alla media data da 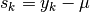 .
.
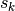 si chiama scarto. Gli scarti formano una successione
si chiama scarto. Gli scarti formano una successione 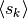 che ha valore medio nullo perché gli scarti di segno positivo compensano quelli
di segno negativo. Per avere un’idea di quanto siano dispersi i valori,
si considera non la media degli scarti, che è
che ha valore medio nullo perché gli scarti di segno positivo compensano quelli
di segno negativo. Per avere un’idea di quanto siano dispersi i valori,
si considera non la media degli scarti, che è  , ma la media
, ma la media 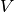 dei loro quadrati: la varianza.
dei loro quadrati: la varianza.
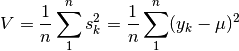
Lo stesso ragionamento, riportato al caso di una funzione continua ![f:[a,b]\to\mathbf{R}](../../../_images/math/a11f00b9981d6439a5bcdf02e4e93ab8df515488.png) con valore medio
con valore medio 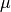 e funzione degli scarti
e funzione degli scarti 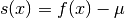 , dà
, dà
![V=\frac{1}{b-a}\int_a^bs(x)^2dx=\frac{1}{b-a}\int_a^b[f(x)-\mu]^2dx](../../../_images/math/a56bf469003cf818fb486a8ccaf1400b798e8225.png)
Avere considerato i quadrati degli scarti evita che lo loro somma sia nulla,
tuttavia dà un risultato medio di natura diversa dalla media della funzione. Per
questo, come misura della dispersione, si preferisce considerare la radice quadrata
della varianza, il cosiddetto scarto quadratico medio 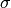 , o
deviazione standard, che si ottiene con le due formule seguenti, valide per il
caso discreto e per il caso continuo:
, o
deviazione standard, che si ottiene con le due formule seguenti, valide per il
caso discreto e per il caso continuo:
![&\sigma=\sqrt{\frac{1}{n-m+1}\sum_m^n(y_k-\mu)^2\Delta x_k}\quad \mbox{, per }f:\{x_k\}_m^n\to \mathbf{R}\\
&\sigma=\sqrt{\frac{1}{b-a}\int_a^b[f(x)-\mu]^2dx}\quad \mbox{, per }f:[a,b]\to \mathbf{R}](../../../_images/math/bb73aacfb3b0874b2698d69a0fc4a692f40e6e10.png)
Applicazioni¶
Per fare esercizio, calcoliamo gli indici di dispersione relativi alle funzioni viste nel Par.8.1.
Nel primo esempio 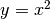 e
e 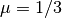 . Allora:
. Allora:
![V=&\frac{1}{1-0}\int_0^1\left(x^2-\frac{1}{3} \right)^2 dx=
\int_0^1\left(x^4-\frac{2}{3}x^2 +\frac{1}{9} \right)=\\
=&\left[\frac{x^5}{5}-\frac{2}{9}x^3+ \frac{1}{9}x\right]_0^1=
\frac{1}{5}+\frac{2}{9}+\frac{1}{9}=\frac{4}{45}.\\
\sigma=&\sqrt{V}=\frac{2}{\sqrt{45}}=0,298.](../../../_images/math/83011ea8406776c3f92bd8a356135e9cfb63d11e.png)
Nel secondo esempio 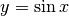 in
in ![[0,\pi]](../../../_images/math/1b989a72aeaf778381894e0025fe309783e17235.png) e
e 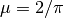 .
.
![V=&\frac{1}{\pi-0}\int_0^\pi\left(\sin x -\frac{2}{\pi} \right)^2 dx=
\frac{1}{\pi}\int_0^\pi\left(\sin^2 x -\frac{4}{\pi}\sin x+ \frac{4}{\pi^2}\right)^2 dx=\\
=&\frac{1}{\pi}\left[\int_0^\pi \sin^2 x dx-\frac{4}{\pi}\int_0^\pi\sin x dx+ \frac{4}{\pi^2} dx\right]=
\frac{1}{\pi}\left(\frac{\pi}{2}-\frac{8}{\pi}+\frac{4}{\pi} \right)=\\
=&\frac{1}{2}-\frac{4}{\pi^2}=0,0947.\\
\sigma=&\sqrt{V}=\sqrt{\frac{1}{2}-\frac{4}{\pi^2}}=0,308.](../../../_images/math/f553b4ab2ca51a12050a31e3d0fc2d3ac5666d6a.png)
Perché proprio i valori quadrati?¶
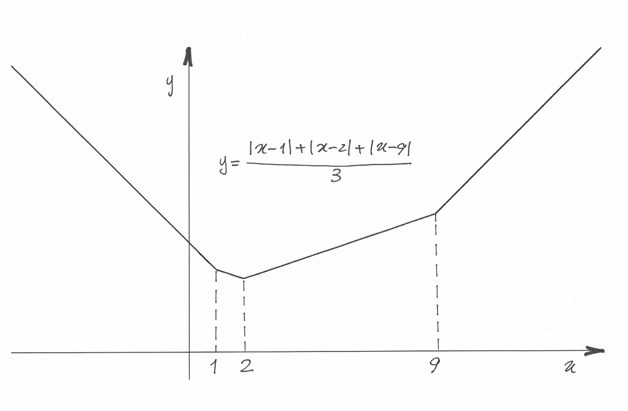
Sarebbe desiderabile usare un indice di dispersione che non comporti il calcolo dei quadrati degli scarti, per poi richiedere la radice quadrata del risultato. Poichè la media degli scarti, presi con il loro segno, vale zero, in effetti si potrebbero considerare gli scarti in valore assoluto, così da sommare sempre valori positivi. La formula allora sarebbe:
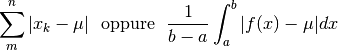
Proviamo a usare questa formula per vedere se è vantaggiosa rispetto alla
deviazione standard. Consideriamo una successione di tre soli valori
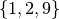 e calcoliamo la media, gli scarti e la loro media
e infine la dispersione nei due modi che stiamo confrontando:
e calcoliamo la media, gli scarti e la loro media
e infine la dispersione nei due modi che stiamo confrontando:
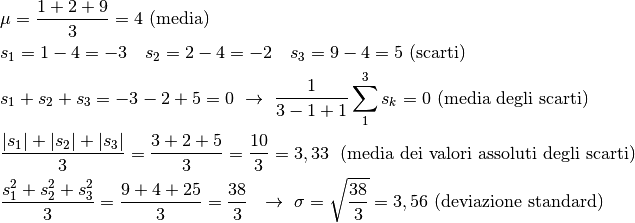
I risultati sono diversi, ma questo non è preoccupante: se tutti usassero come indice della dispersione la media dei valori assoluti degli scarti, il fatto che la deviazione standard dia un risultato diverso non importerebbe. Dobbiamo capire quindi se ci sono particolari vantaggi nell’adottare un calcolo o l’altro per i nostri scopi. Il fatto di dover calcolare anche una radice quadrata in fondo è un dettaglio sopportabile, se la scelta è vantaggiosa.
Per una valutazione più generale, calcoliamo gli scarti rispetto a un qualsiasi
valore  , anche diverso da
, anche diverso da 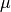 . Studiamo cioè la funzione
. Studiamo cioè la funzione
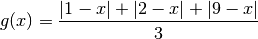
Per 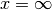 la funzione assume valori infiniti. Lo stesso avviene per
la varianza
la funzione assume valori infiniti. Lo stesso avviene per
la varianza
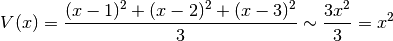
e di conseguenza anche la deviazione standard, che è 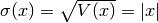 ,
per valori infiniti assume valori infiniti, di modo che
,
per valori infiniti assume valori infiniti, di modo che
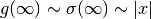 . All’infinito le due funzioni hanno
lo stesso comportamento asintotico. Ci aspettiamo che esista
anche un valore di
. All’infinito le due funzioni hanno
lo stesso comportamento asintotico. Ci aspettiamo che esista
anche un valore di  per il quale le due funzioni hanno un minimo, come
accade a tutte le funzioni continue. Cerchiamo ora questo minimo.
per il quale le due funzioni hanno un minimo, come
accade a tutte le funzioni continue. Cerchiamo ora questo minimo.
Nel caso di 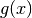 distinguiamo i casi e poi procediamo per via grafica.
distinguiamo i casi e poi procediamo per via grafica.
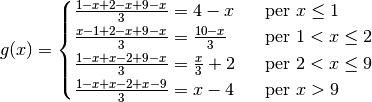
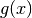 ha quindi il minimo in
ha quindi il minimo in 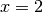 , dove assume il valore
, dove assume il valore 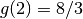 .
.
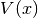 è una funzione ovunque derivabile. Cerchiamo il minimo di
è una funzione ovunque derivabile. Cerchiamo il minimo di 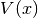 invece di quello di
invece di quello di 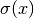 per semplicità di calcoli, dato che le due
funzioni devono avere minimo per lo stesso valore di
per semplicità di calcoli, dato che le due
funzioni devono avere minimo per lo stesso valore di  .
.
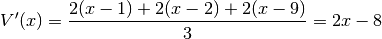
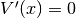 per
per 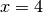 . Il risultato suggerisce l’idea che la deviazione
standard abbia minimo assoluto in corrispondenza della media dei valori.
Se questo risultato non è casuale, si tratta di una proprietà rilevante, da
approfondire. Per farlo, studiamo il caso generale.
. Il risultato suggerisce l’idea che la deviazione
standard abbia minimo assoluto in corrispondenza della media dei valori.
Se questo risultato non è casuale, si tratta di una proprietà rilevante, da
approfondire. Per farlo, studiamo il caso generale.
Consideriamo una successione 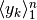 e cerchiamo il valore
per il quale la varianza è minima. Perciò scriviamo la funzione
e cerchiamo il valore
per il quale la varianza è minima. Perciò scriviamo la funzione 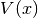 ,
ne calcoliamo la derivata e cerchiamo il valore per cui si annulla:
,
ne calcoliamo la derivata e cerchiamo il valore per cui si annulla:
![&V(x)=\frac{1}{n}\sum_1^n(x-y_k)^2\\
&V'(x)=\frac{1}{n}\sum_1^n2(x-y_k)=\frac{2}{n}\left[\sum_1^n x-\sum_1^n y_k \right]=
\frac{2}{n}\left[n x-\sum_1^n y_k \right]\\
&V'(x)=0\ \to \ n x=\sum_1^n y_k\ \to \ x=\frac{1}{n}\sum_1^n y_k=\mu](../../../_images/math/83ba2b43e838b4cac097fbef3f6865edda4554b5.png)
Si tratta di una proprietà generale: la varianza, e di conseguenza la deviazione standard, sono funzioni che hanno il minimo assoluto in coincidenza del valore medio. Sono quindi funzioni particolarmente indicate per esprimere la dispersione dei valori attorno alla media.
Il baricentro¶
Il baricentro è un punto particolarmente importante di un corpo o di un sistema di masse: è un punto di equilibrio per la distribuzione delle masse del corpo. Il calcolo della posizione del baricentro coinvolge il concetto di media e per questo ce ne occupiamo qui. A rigore, si usa distinguere il baricentro (letteralmente: centro dei pesi) dal centro di massa, ma la distinzione diventa significativa se masse uguali del sistema hanno peso diverso. Questo potrebbe accadere per esempio se due masse identiche sono collocate una vicino alla superficie terrestre e l’altra molto lontano, cosa che non è abituale. Quindi, nel seguito del nostro discorso, useremo il termine baricentro come se coincidesse con il centro di massa.
Il caso discreto¶
Iniziamo da un caso semplice, nel discreto. Due masse 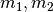 sono
collocate nei punti
sono
collocate nei punti 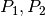 , di posizione
, di posizione 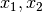 .
Il baricentro è il punto
.
Il baricentro è il punto 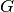 , di coordinata
, di coordinata 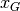 , che divide
il segmento
, che divide
il segmento 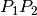 in parti inversamente proporzionali alle masse.
Cioè:
in parti inversamente proporzionali alle masse.
Cioè:
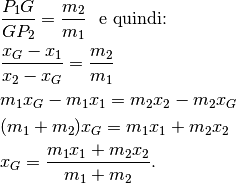
Si tratta della media pesata delle coordinate: ogni coordinata viene contata tante volte quante sono indicate dalla massa che vi risiede.
Il concetto si estende al caso di 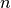 punti
punti 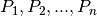 di coordinate
di coordinate 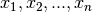 , con masse
, con masse 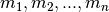 .
.
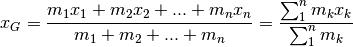
Una proprietà importante di questa formula è l’additività: il baricentro non
cambia se all’interno del sistema si isolano due o più gruppi di termini e
nella formula si inseriscono al loro posto le loro masse complessive
e loro baricentri. In pratica significa che ogni sistema di masse può
essere pensato come concentrato nel suo baricentro. Ecco i calcoli,
per un sistema di 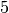 masse:
masse:
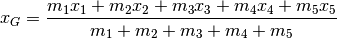
Calcoliamo ora i baricentri 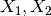 di due diversi sottosistemi: il
primo è costituito dalle prime tre masse, il secondo dalle altre due. Al
termine calcoliamo il baricentro del sistema dei due baricentri.
di due diversi sottosistemi: il
primo è costituito dalle prime tre masse, il secondo dalle altre due. Al
termine calcoliamo il baricentro del sistema dei due baricentri.
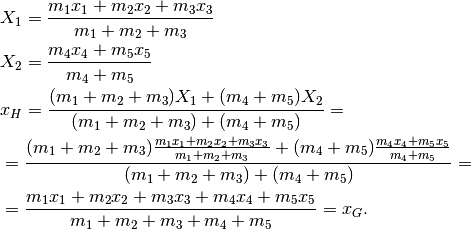
Il caso continuo¶
Pensiamo una barra omogenea di lunghezza 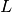 . Il suo modello geometrico
è un segmento
. Il suo modello geometrico
è un segmento ![[0,L]](../../../_images/math/0ed2ff58ba619efee64e6030e2b127eb4d07fb05.png) . Se la barra è sottile e omogenea, la
massa è distribuita ugualmente in tutta la lunghezza e il baricentro si trova
necessariamente in
. Se la barra è sottile e omogenea, la
massa è distribuita ugualmente in tutta la lunghezza e il baricentro si trova
necessariamente in 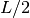 . Se la massa è omogenea, in ogni punto la massa
ha densità media, data dal rapporto
. Se la massa è omogenea, in ogni punto la massa
ha densità media, data dal rapporto
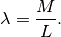
Se la massa non è omogenea, la densità varia da punto a punto e abbiamo
bisogno di una descrizione dettagliata di come la densità è distribuita lungo la
barra. La massa è quindi una funzione della distanza da un estremo:
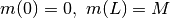 . Dividiamo la lunghezza della barra in
. Dividiamo la lunghezza della barra in 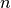 parti
mediante i punti di suddivisione
parti
mediante i punti di suddivisione 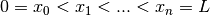 e consideriamo
la massa di ogni parte
e consideriamo
la massa di ogni parte 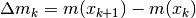 e la densità lineare
media di quel tratto come
e la densità lineare
media di quel tratto come 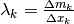 .
Come primo approccio possiamo pensare che i punti siano in progressione aritmetica
e quindi le porzioni di barra siano di uguale lunghezza. Ma la suddivisione può
diventare più fitta e, come abbiamo già visto in tanti altri casi, la
funzione che descrive la densità ha un grafico a scalini che si avvicina ad
una curva continua.
.
Come primo approccio possiamo pensare che i punti siano in progressione aritmetica
e quindi le porzioni di barra siano di uguale lunghezza. Ma la suddivisione può
diventare più fitta e, come abbiamo già visto in tanti altri casi, la
funzione che descrive la densità ha un grafico a scalini che si avvicina ad
una curva continua.
La massa è rappresentata dall’area sottesa al grafico della densità, e si ottiene da
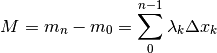
che rispecchia il teorema fondamentale del calcolo delle somme.
Se invece affiniamo l’analisi della densità lineare, dandone una descrizione
punto per punto, in modo che 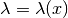 , allora possiamo dividere
la barra in tratti infiniresimi
, allora possiamo dividere
la barra in tratti infiniresimi ![[x,x+dx]](../../../_images/math/7fd8b77420413377b5c15e07665dceb1fa6465a7.png) , ciascuno com massa
, ciascuno com massa
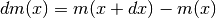 . La densità in ogni punto sarà allora la parte standard
del rapporto differenziale
. La densità in ogni punto sarà allora la parte standard
del rapporto differenziale
![st\left[\frac{dm(x)}{dx}\right]=\left[\frac{m(x+dx)-m(x)}{dx}\right]=m'(x).](../../../_images/math/3dc4ff7088bc24edac5025e1ec83350bfe759a8f.png)
Nel caso continuo, la massa della parte di barra definita dall’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) si può esprimere in due modi: sia come
si può esprimere in due modi: sia come 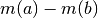 , cioè come
differenza fra le masse relative a
, cioè come
differenza fra le masse relative a ![[0,b]](../../../_images/math/dcdd994c8578367ecdce1a5e316169cd71160233.png) e
e ![[0,a]](../../../_images/math/49da8af216f71dca04c3f6ecc108ea8b991d433c.png) , sia come
, sia come
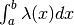 . Questo corrisponde, ovviamente, al teorema
fondamentale del calcolo integrale nel caso continuo:
. Questo corrisponde, ovviamente, al teorema
fondamentale del calcolo integrale nel caso continuo:
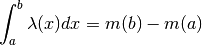
Possiamo dare un’immagine geometrica della densità lineare variabile: stiriamo la barra in senso trasversale, in modo da trasformarla in una lastra dal profilo ondulato. La stiriamo maggiormente dove la massa era più concentrata, e quindi la densità era maggiore, e così facendo otteniamo una lastra omogenea, cioè con densità uguale in tutti punti. In questo modo, quello che prima era il profilo della densità ora è diventato il profilo della lastra e l’area della lastra corrisponde alla massa della barra.
Il baricentro della barra si calcola, allora, come la media pesata, rispetto alla massa, delle posizioni delle varie masse. Cioè:
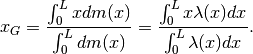
Due esempi¶
- Calcola il baricentro del segmento
![[0,2]](../../../_images/math/0d3e992e11627ec756395967c4f8bbab66cc2a67.png) , sapendo che la densità cresce secondo
la funzione quadratica:
, sapendo che la densità cresce secondo
la funzione quadratica: 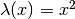 .
.
Per prima cosa calcoliamo la massa totale, poi il baricentro.
![&M=\int_0^2\lambda(x)dx=\int_0^2x^2dx=\left[\frac{x^3}{3} \right]_0^2=\frac{8}{3}\\
&\int_0^2x\lambda(x)dx=\int_0^2x^3dx=\left[\frac{x^4}{4} \right]_0^2=\frac{16}{4}=4\\
&x_G=\frac{4}{8/3}=\frac{3}{2}.](../../../_images/math/e4ed6c32542cd34f36a6b534c2e1a217bd7c4379.png)
Dato che la densità cresce secondo 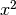 , la massa sarà più concentrata
nella zona destra del segmento e quindi è giusto che il baricentro si trovi oltre
il punto medio.
, la massa sarà più concentrata
nella zona destra del segmento e quindi è giusto che il baricentro si trovi oltre
il punto medio.
- Calcola il baricentro del segmento
![\left[0,\frac{\pi}{2}\right]](../../../_images/math/458a7a49f3e3ce0fb27ba788808a67b5215b483f.png) , sapendo
che la massa cresce secondo la funzione
, sapendo
che la massa cresce secondo la funzione 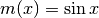 .
.
Note
La funzione 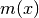 che rappresenta la massa è positiva e non può
decrescere, nell’intervallo considerato. Si tratta di un’evidenza
fisica: la massa è
che rappresenta la massa è positiva e non può
decrescere, nell’intervallo considerato. Si tratta di un’evidenza
fisica: la massa è  all’estremo iniziale del segmento e poi
progressivamente si aggiunge, o per lo meno non decresce, anche se la
densità può diminuire.
all’estremo iniziale del segmento e poi
progressivamente si aggiunge, o per lo meno non decresce, anche se la
densità può diminuire.
Questa volta la massa cresce sempre più lentamente nell’intervallo considerato e quindi il baricentro deve trovarsi nella prima metà del segmento. La soluzione:
![&M=\int_0^{\frac{\pi}{2}}d\sin x=[\sin x]_0^{\frac{\pi}{2}}=1\\
&x_G=\int_0^{\frac{\pi}{2}}xd\sin x=[x\sin x]_0^{\frac{\pi}{2}}
-\int_0^{\frac{\pi}{2}}\sin xdx=\frac{\pi}{2}-1=0,57.](../../../_images/math/90450b2b498fb97f4b9404363b9c9453a822cbb0.png)
Ovviamente, nella formula per il calcolo di 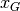 manca il denominatore,
dato il risultato della riga precedente.
manca il denominatore,
dato il risultato della riga precedente.
Il baricentro di una figura piana¶
Iniziamo da un trapezoide, cioè una regione piana, limitata dal grafico di una
funzione, in questo caso nel primo quadrante:
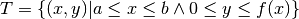 , con
, con ![f:[a,b]\to \mathbf{R}](../../../_images/math/b1987d338915627988b2ad15b000206c66ca022b.png) .
.
Per semplificare il problema, dobbiamo pensare di riferirci ad una lastra piana
omogenea, cioè con la massa ugualmente distribuita e quindi con un rapporto,
fra la massa di una qualsiasi porzione e l’area della sua superficie,
sempre costante e uguale al rapporto medio, detto densità superficiale 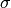 :
:
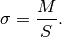
Per determinare il baricentro dividiamo la superficie in strisce verticali di
larghezza infinitesima 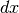 , di altezza
, di altezza  e di massa
e di massa
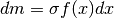 . La media pesata delle ascisse ci dà l’ascissa del
baricentro:
. La media pesata delle ascisse ci dà l’ascissa del
baricentro:
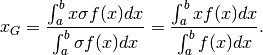
Trattandosi del baricentro di una superficie, ci serve anche la seconda dimensione.
Nel caso verticale però la suddivisione dell’intervallo non è in parti infinitesime,
perché ogni striscia ha altezza pari a  . Però ha larghezza infinitesima
e quindi può essere considerata come un segmento omogeneo di lunghezza
. Però ha larghezza infinitesima
e quindi può essere considerata come un segmento omogeneo di lunghezza  .
Il baricentro di una striscia si trova perciò a metà altezza e la coordinata
.
Il baricentro di una striscia si trova perciò a metà altezza e la coordinata 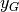 si calcola come media pesata di
si calcola come media pesata di 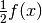 su tutto l’intervallo:
su tutto l’intervallo:
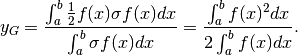
È da notare che la densità 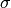 si semplifica nei calcoli e questo ha
un senso perché la lastra piana è omogenea e perciò contano solo le questioni
geometriche.
si semplifica nei calcoli e questo ha
un senso perché la lastra piana è omogenea e perciò contano solo le questioni
geometriche.
Vediamo qualche applicazione.
Il baricentro di un semicerchio¶
Consideriamo il semicerchio definito nel semipiano superiore dalla circonferenza
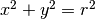 . La funzione del trapezoide allora sarà
. La funzione del trapezoide allora sarà 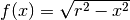 ,
con
,
con 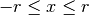 . Per ragioni di simmetria, è inutile svolgere i calcoli per
. Per ragioni di simmetria, è inutile svolgere i calcoli per
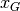 : è ovvio che
: è ovvio che 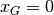 . Quanto a
. Quanto a 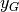 , calcoliamo
separatamente il numeratore e il denominatore della formula precedente:
, calcoliamo
separatamente il numeratore e il denominatore della formula precedente:
![\int_a^b f(x)^2dx=\int_{-r}^r (r^2-x^2)dx=\left[r^2x-\frac{x^3}{3} \right]_{-r}^r=
\frac{4}{3}r^3.](../../../_images/math/60ada8b7431fbac598b2aa3b466704a2c63e0a87.png)
L’integrale del denominatore, che fornisce la superficie del semicerchio, viene
lasciato per esercizio. In ogni caso il risultato non può che essere 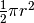 .
Alla fine abbiamo:
.
Alla fine abbiamo:
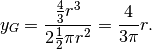
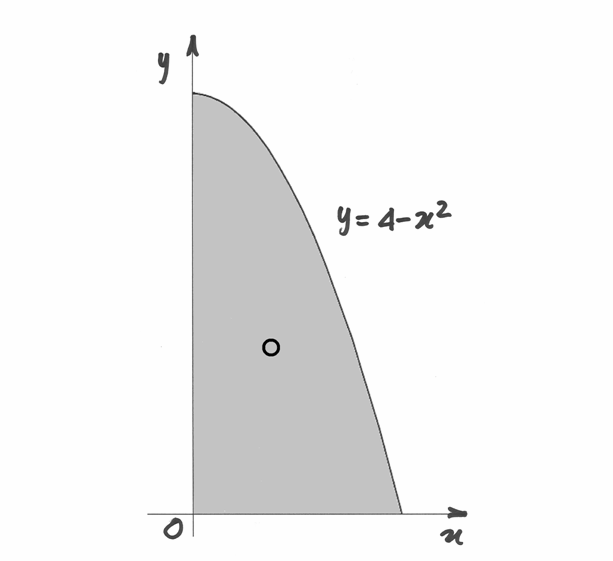
Il baricentro di un trapezoide parabolico¶
Cerchiamo il baricentro del trapezoide compreso, nel primo quadrante,
fra il grafico della funzione 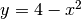 e gli assi cartesiani.
Questa volta occorre calcolare entrambe le coordinate. Per l’ascissa:
e gli assi cartesiani.
Questa volta occorre calcolare entrambe le coordinate. Per l’ascissa:
![&\int_a^b f(x)dx=\int_0^2(4-x^2)dx=\left[4x-\frac{x^3}{3}\right]_0^2=\frac{16}{3}.\\
&\int_a^b xf(x)dx=\int_0^2(4x-x^3)dx=\left[2x^2-\frac{x^4}{4}\right]_0^2=4.\\
&x_G=\frac{\int_a^bx f(x)dx}{\int_a^b f(x)dx}=\frac{4}{\frac{16}{3}}=\frac{3}{4}.](../../../_images/math/5f25582e946cb4251523e048452267d5fd8d7279.png)
Per l’ordinata:
![&\int_a^bf(x)^2dx= \int_0^2(4-x^2)^2dx= \int_0^2f(16-8x^2+x^4)dx=
\left[16x-\frac{8x^3}{3}+\frac{x^5}{5} \right]_0^2=\frac{256}{15}.\\
&y_G=\frac{\int_a^b f(x)^2dx}{2\int_a^b f(x)dx}=
\frac{\frac{256}{15}}{\frac{32}{3}}=\frac{8}{5}.](../../../_images/math/cbb23c920aa6f9c960ab7f334369b39d5b33437f.png)
Quindi il baricentro si trova nel punto 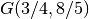 .
.
Il baricentro di un grafico¶
Pensiamo al grafico di una funzione come a un filo omogeneo disteso nel piano
cartesiano. Se consideriamo un intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , la lunghezza
, la lunghezza 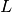 del filo sarà
del filo sarà 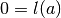 al primo estremo e pari a
al primo estremo e pari a 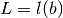 al secondo,
dove la funzione
al secondo,
dove la funzione 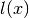 esprime la lunghezza del filo nel punto
esprime la lunghezza del filo nel punto  dell’intervallo. Definiamo anche con
dell’intervallo. Definiamo anche con 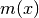 la funzione che esprime la
massa del grafico nel punto
la funzione che esprime la
massa del grafico nel punto  , a partire da
, a partire da 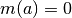 . Il filo è
omogeneo, quindi la massa è distribuita uniformemente e la densità lineare
. Il filo è
omogeneo, quindi la massa è distribuita uniformemente e la densità lineare
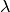 è costante e uguale alla densità media
è costante e uguale alla densità media
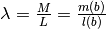 .
.
Per determinare il baricentro del grafico, dividiamo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) in infiniti
intervallini infinitesimi di ampiezza
in infiniti
intervallini infinitesimi di ampiezza 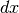 . Le coordinate del baricentro
del grafico sono allora le medie pesate delle coordinate dei tratti infinitesimi.
Il tratto che va da
. Le coordinate del baricentro
del grafico sono allora le medie pesate delle coordinate dei tratti infinitesimi.
Il tratto che va da  a
a 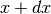 ha una lunghezza
ha una lunghezza 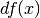 e
una massa
e
una massa 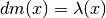 · Il suo baricentro è infinitamente vicino al
punto
· Il suo baricentro è infinitamente vicino al
punto 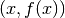 . Quindi:
. Quindi:
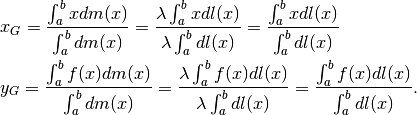
Se la funzione è derivabile, allora il tratto infinitesimo 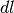 del grafico
è indistinguibile da un tratto rettilineo:
del grafico
è indistinguibile da un tratto rettilineo:
^2.](../../../_images/math/a160557246fcc7cf6b443d4de390e2eea6cabf1a.png)
Ne segue che 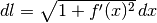 e la lunghezza del grafico è:
e la lunghezza del grafico è:
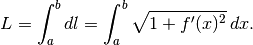
Moltiplicando 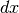 per il coefficiente
per il coefficiente 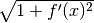 si ottiene
la lunghezza infinitesima
si ottiene
la lunghezza infinitesima 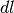 del tratto di grafico. Passiamo cioè dalla
lunghezza del tratto orizzontale a quella del tratto, che in genere è obliquo,
attraverso un coefficiente di dilatazione contenente la derivata. Infatti
(e ovviamente se la funzione è derivabile), maggiore è il valore della derivata
e maggiore è la lunghezza del tratto di grafico in rapporto alla lunghezza
del tratto di grafico. Passiamo cioè dalla
lunghezza del tratto orizzontale a quella del tratto, che in genere è obliquo,
attraverso un coefficiente di dilatazione contenente la derivata. Infatti
(e ovviamente se la funzione è derivabile), maggiore è il valore della derivata
e maggiore è la lunghezza del tratto di grafico in rapporto alla lunghezza 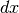 .
Per fare un esempio, se il grafico in quella posizione fosse un segmento inclinato
di
.
Per fare un esempio, se il grafico in quella posizione fosse un segmento inclinato
di 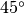 , la derivata varrebbe
, la derivata varrebbe 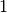 e il coefficiente
e il coefficiente 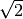 .
Le equazioni per il baricentro sono allora:
.
Le equazioni per il baricentro sono allora:
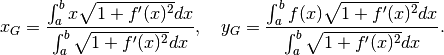
Baricentro di una semicirconferenza¶
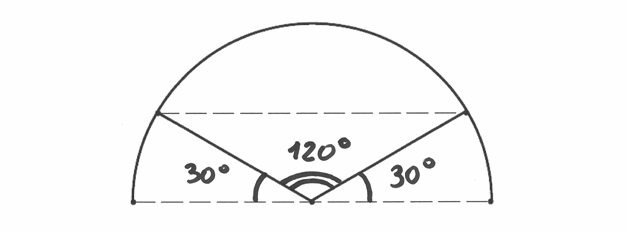
Cerchiamo il baricentro della funzione
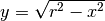
Data la simmetria del grafico, il baricentro si trova sull’asse  e dobbiamo calcolare solo
e dobbiamo calcolare solo  . Procediamo con ordine, un calcolo dopo
l’altro, fino al risultato.
. Procediamo con ordine, un calcolo dopo
l’altro, fino al risultato.
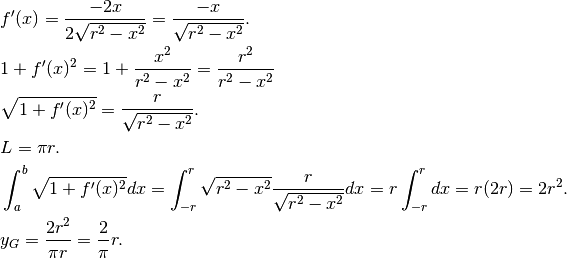
Si vede anche dal disegno che la posizione verticale del baricentro deve superare la metà del raggio, perchè l’arco superiore è lungo il doppio dei due archi laterali.
Riassunto¶
La media fra più numeri è quel valore che tutti loro avrebbero, se fossero uguali. Si calcola sommando i numeri e dividendo poi la somma per quanti sono i valori da sommare.
La media di una successione
 è data da
è data da
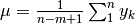 .
.  è detto valore medio
della successione.
è detto valore medio
della successione.Per una funzione a dominio discreto:
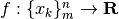 , con
, con
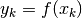 , il valore medio:
, il valore medio: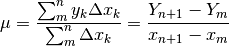
L’ultima uguaglianza deriva dal teorema fondamentale del calcolo delle somme.
Nelle funzioni continue
![f:[a,b]\to \mathbf{R}](../../../_images/math/86bbcc1e6fd1ad5fca5cf93f9037be22a7432370.png) , il valore medio è dato da
, il valore medio è dato da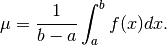
che corrisponde, per il teorema fondamentale del calcolo integrale, a
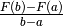 . L’interpretazione geometrica del valore medio
è la seguente: il valore medio di una funzione è l’altezza del rettangolo, di
base
. L’interpretazione geometrica del valore medio
è la seguente: il valore medio di una funzione è l’altezza del rettangolo, di
base ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , equiesteso alla regione di piano sottesa al grafico della
funzione.
, equiesteso alla regione di piano sottesa al grafico della
funzione.Se la funzione è continua, nell’intervallo dato assume almeno una volta il suo valore medio, che è compreso fra il minimo e il massimo dei valori che la funzione assume nell’intervallo. Mentre una funzione a dominio discreto non è detto che assuma il suo valore medio.
La deviazione standard
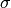 è un indice di quanto la distribuzione
dei valori è dispersa. Si calcola secondo le seguenti formule, adatte al caso
discreto e al caso continuo
è un indice di quanto la distribuzione
dei valori è dispersa. Si calcola secondo le seguenti formule, adatte al caso
discreto e al caso continuo![&\sigma=\sqrt{\frac{1}{n-m+1}\sum_m^n(y_k-\mu)^2\Delta x_k}
\quad \mbox{, per }f:\{x_k\}_m^n\to \mathbf{R}\\
&\sigma=\sqrt{\frac{1}{b-a}\int_a^b[f(x)-\mu]^2dx}
\quad \mbox{, per }f:[a,b]\to \mathbf{R}](../../../_images/math/a25d83db6cb1783db808df9f7a528279a5c51b8c.png)
Rispetto a altri indici di dispersione, uno dei pregi maggiori di
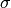 è che viene calcolata rispetto al valore medio della funzione e per questo ha
valore minimo.
è che viene calcolata rispetto al valore medio della funzione e per questo ha
valore minimo.Il baricentro di un sistema di masse è un punto di equilibrio per il sistema. La posizione delle masse rispetto a questo punto teorico viene contata tante volte quante è indicato dal valore della massa. Si tratta infatti di una media pesata. Nei casi ordinari baricentro e centro di massa sono equivalenti.
Nel caso discreto, di un sistema di
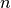 masse allineate su una retta, si ha:
masse allineate su una retta, si ha: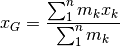
Una delle proprietà della formula è l’additività: isolando un gruppo di masse all’interno del sistema, nel calcolo della posizione del baricentro si può inserire il baricentro del gruppo al posto di queste masse.
Il baricentro di una distribuzione continua di masse dipende da quale densità ha la massa nelle varie posizioni. Per una distribuzione lineare si ha:
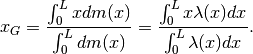
dove
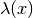 è la densità lineare.
è la densità lineare.Nel caso di una distribuzione omogenea (cioè di densità costante
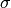 )
di masse in una superficie, trovare il baricentro è come trovare il centro
geometrico della figura piana che contiene le masse. La posizione del baricentro
è
)
di masse in una superficie, trovare il baricentro è come trovare il centro
geometrico della figura piana che contiene le masse. La posizione del baricentro
è 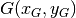 .
.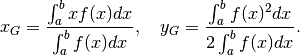
Si può calcolare il baricentro anche per il grafico di una funzione su un intervallo
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) . Le formule sono:
. Le formule sono: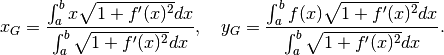
Esercizi¶
- Inventa una successione di tre valori aventi per media
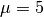 e ripeti i
calcoli del paragrafo 3 per verificare che
e ripeti i
calcoli del paragrafo 3 per verificare che 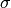 è un indice della
dispersione vantaggioso rispetto alla media dei valori assoluti degli scarti.
è un indice della
dispersione vantaggioso rispetto alla media dei valori assoluti degli scarti.
.png)