Integrali notevoli¶
Integrali notevoli¶
Ricaviamo le primitive di alcune funzioni notevoli. Si tratta di integrali in genere piuttosto difficili, il cui calcolo ci serve per esemplificare l’uso combinato di più tecniche risolutive.
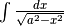 ¶
¶
Prima di affrontare il caso generale, iniziamo da un esempio:
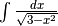 .
L’integrale ricorda
.
L’integrale ricorda 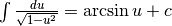 . Lo possiamo
utilizzare con questa semplice tecnica:
. Lo possiamo
utilizzare con questa semplice tecnica:
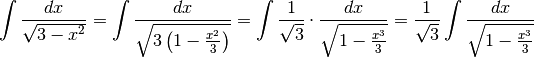
Poniamo 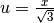 , da cui
, da cui 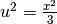 . Quindi
. Quindi
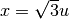 e
e 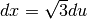 .
.
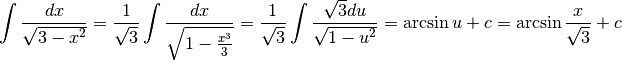
Da questo calcolo risaliamo alla formula che vale per
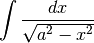
con 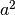 necessariamente positivo.
necessariamente positivo.
Dato che
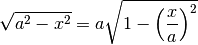
usiamo le seguenti posizioni 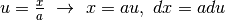
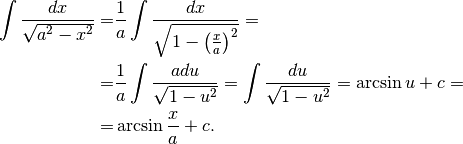
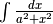 ¶
¶
Con la solita tecnica, raccogliere al denominatore il primo addendo e poi usare le sostituzioni dell’esercizio precedente, si ha:
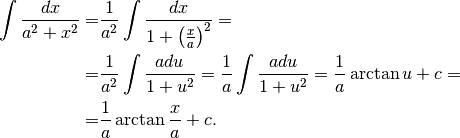
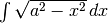 ¶
¶
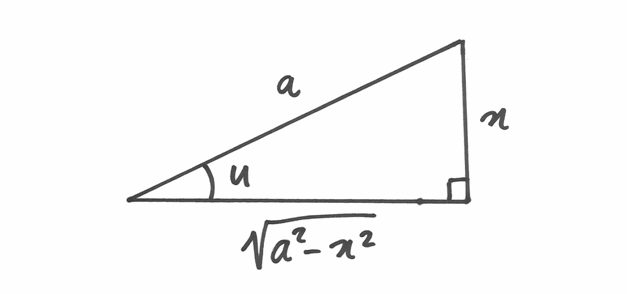
La funzione integranda corrisponde geometricamente alla misura  di un
cateto, in un triangolo rettangolo con l’ipotenusa di lunghezza
di un
cateto, in un triangolo rettangolo con l’ipotenusa di lunghezza  . È
utile operare una sostituzione dopo avere indicato con
. È
utile operare una sostituzione dopo avere indicato con 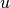 l’angolo
opposto al lato di misura
l’angolo
opposto al lato di misura  .
.
Avremo 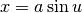 ,
, 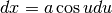 e
e 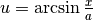 .
.
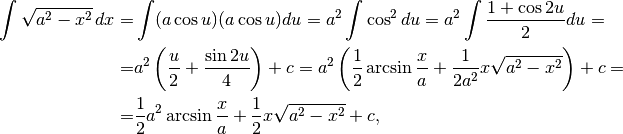
dato che: 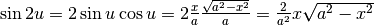 .
.
C’è un ragionamento geometrico che conduce alla stessa soluzione.
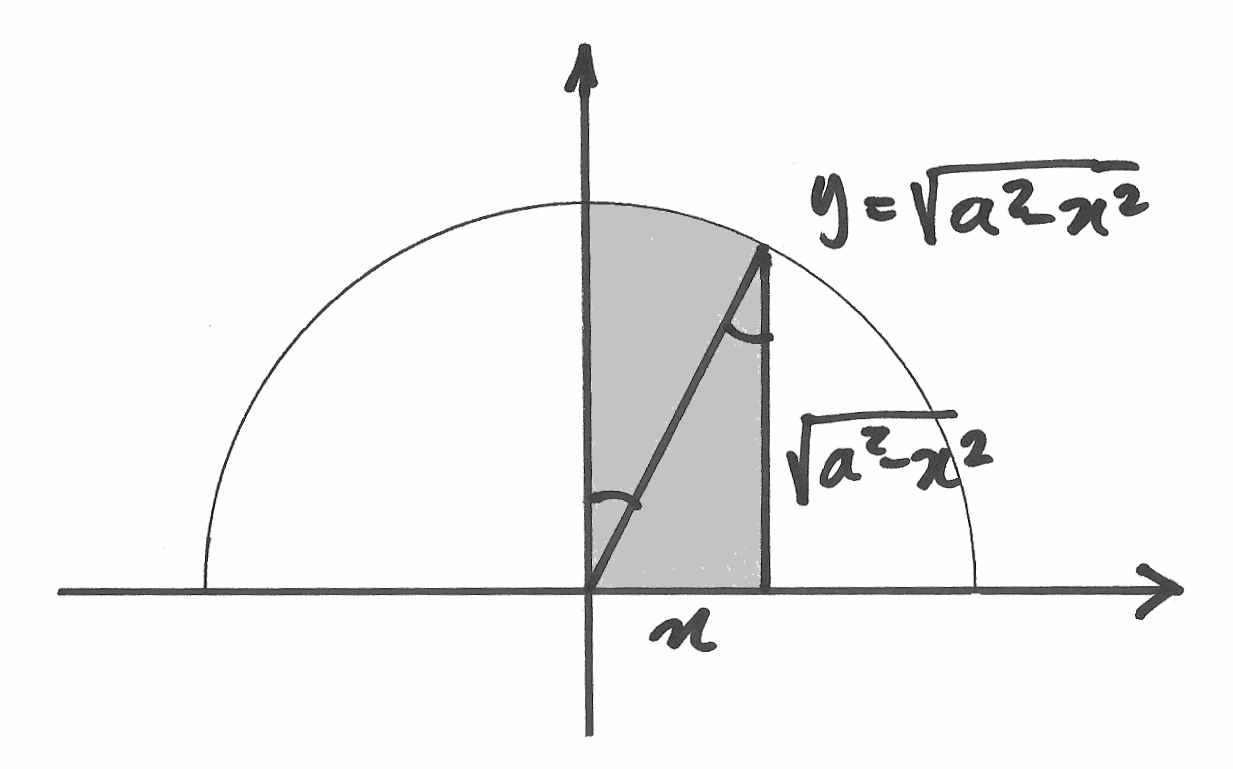
La funzione 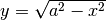 rappresenta, per
rappresenta, per 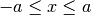 , la
semicirconferenza positiva di raggio
, la
semicirconferenza positiva di raggio  , centrata nell’origine. L’integrale
ha quindi, come una delle primitive, l’area del semicerchio che , per
, centrata nell’origine. L’integrale
ha quindi, come una delle primitive, l’area del semicerchio che , per 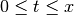 ,
vale
,
vale
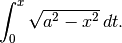
L’area in questione è l’area di due figure: un triangolo di base  e altezza
e altezza
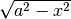 e un settore di angolo
e un settore di angolo 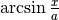 . Le aree
delle due figure sono
. Le aree
delle due figure sono 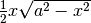 e
e
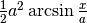 . Così abbiamo che
. Così abbiamo che
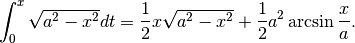
Questa è una particolare primitiva. Per ottenere il risultato generale
basta aggiungere  .
.
Note
Questa soluzione esemplifica un metodo: se l’integrale indefinito è difficile
da calcolare, si può procedere alla ricerca di una primitiva per via geometrica,
attraverso il calcolo dell’area sottesa alla curva nell’intervallo ![[0,x]](../../../_images/math/90dfc020d493988ead9effbec6499d200a315545.png) e poi si generalizza il risultato.
e poi si generalizza il risultato.
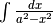 ¶
¶
In questi integrali è opportuna una trasformazione algebrica:
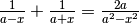 , per cui:
, per cui:
![&\int\frac{dx}{a^2-x^2}=\frac{1}{2a}\left[\int\frac{dx}{a-x}+\int\frac{dx}{a+x}\right]](../../../_images/math/6ccc56fe3b4cc8a79d05c49a7bf4852eeb7a829d.png)
Poniamo per il primo integrale 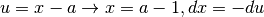 , quindi:
, quindi:
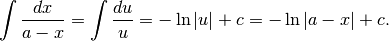
Per il secondo integrale: 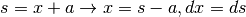 , quindi:
, quindi:
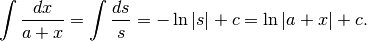
In conclusione:
![\int\frac{dx}{a^2-x^2}=&
\frac{1}{2a}\left[\int\frac{dx}{a-x}+\int\frac{dx}{a+x}\right]=\\
=&\frac{1}{2a}\left(-\ln|a-x|+\ln|a+x|\right)+c =
\frac{1}{2a}\ln\left|\frac{a+x}{a-x}\right|+c=\\
=&\frac{1}{2a}\ln\left|\frac{x+a}{x-a}\right|+c.](../../../_images/math/e8774f3e6f4044acf3e89e2ba6f026105f11ef34.png)
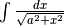 ¶
¶
Potremmo ricorrere di nuovo al triangolo rettangolo, ma, per cambiare, calcoliamo
questo integrale con una sostituzione diversa dalle solite.
Poiché 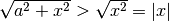 , risulta
, risulta 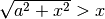 e
quindi è sempre positiva la differenza
e
quindi è sempre positiva la differenza 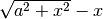 .
La sostituzione è:
.
La sostituzione è: 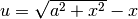 , da cui
, da cui 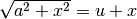 .
Per sostituire
.
Per sostituire  e
e 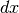 svolgiamo i passaggi seguenti:
svolgiamo i passaggi seguenti:
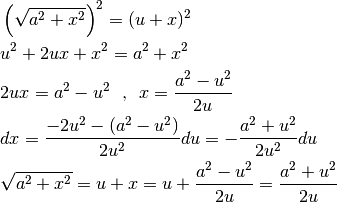
Ora possiamo integrare:
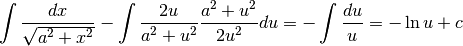
(ricordiamo che 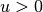 ).
).
Siccome
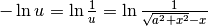 , razionalizzando
otteniamo:
, razionalizzando
otteniamo:
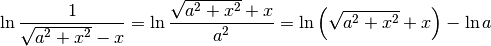
e così, finalmente:
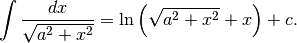
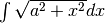 ¶
¶
Anche in questo caso sarebbe utile ricorrere al Teorema di Pitagora, ma vogliamo insistere con tecniche algebriche. Questa volta integriamo per parti e ricordiamo il risultato precedente.
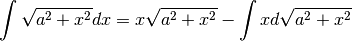
Consideriamo che
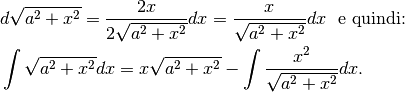
Ora, manipoliamo algebricamente:
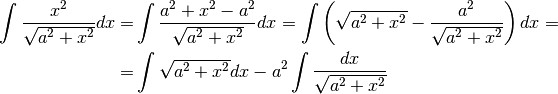
e possiamo concludere con i passaggi seguenti:
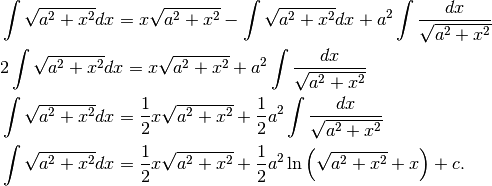
Note
Questi esercizi sono stati illustrati a scopo dimostrativo. Non si pretende che lo studente arrivi a questo livello di difficoltà, anche perché questi e altri integrali anche molto più complessi si possono risolvere usando software dedicato di larga diffusione. Allo studente resta il compito di imparare a memoria gli integrali immediati e di tenere a disposizione l’elenco di quelli notevoli, per avere un riferimento in caso di difficoltà.
Ulteriori casi notevoli¶
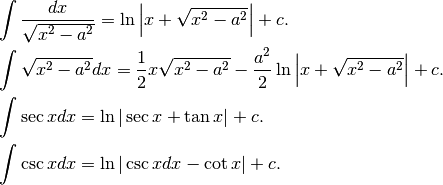
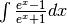 ¶
¶
Operiamo la sostituzione 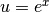 , da cui
, da cui 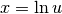 e
e 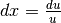 Abbiamo quindi:
Abbiamo quindi:
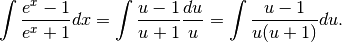
Nell’esempio 7.1.4 avevamo un caso simile a questo: il denominatore era, come adesso, un prodotto e abbiamo trasformato l’espressione in modo da separare i due fattori. Cerchiamo quindi di definire due frazioni, la cui somma dia la funzione integranda. Non conoscendo i numeratori, al loro posto indichiamo due costanti generiche. La tecnica è la seguente:
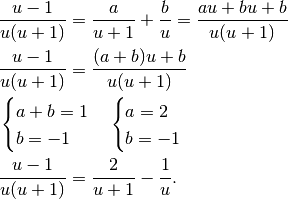
ora possiamo integrare facilmente:
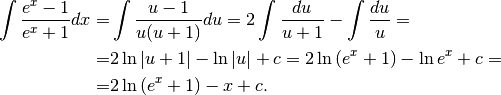
I valori assoluti non servono perché gli argomenti sono positivi.
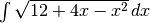 ¶
¶
Fra gli esercizi precedenti, quello che meglio si adatta a risolvere quest’ultimo
è l’es.7.1.4. Cerchiamo quindi di trasformare la funzione integranda in modo
da seguire lo schema di quell’esercizio. Osserviamo che 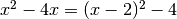 ,
per cui
,
per cui
![12+4x-x^2=12-(x^2-4x)=12-[(x-2)^2-4]=16-(x-2)^2](../../../_images/math/d39ef41a34a8e574418cb4e79bdac7da40220c44.png)
Ponendo 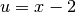 , si ha:
, si ha:
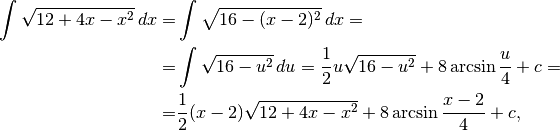
in cui si è fatto uso del risultato dell’es.7.1.4.
Integrare le funzioni inverse¶
All’inizio concentriamoci su un paio di esempi, per introdurre poi la regola generale.
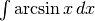 ¶
¶
- Proviamo a integrare per parti:
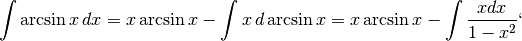
A questo punto sembra utile la sostituzione 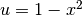 , che comporta i
passaggi seguenti:
, che comporta i
passaggi seguenti:
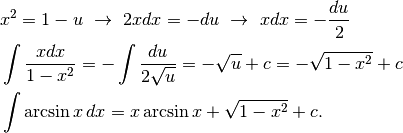
- Cambiamo strategia: proviamo subito la sostituzione:
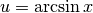 , per cui
, per cui
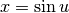 e
e 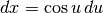 . Ne consegue
. Ne consegue
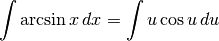
Siamo al punto di dover integrare per parti:
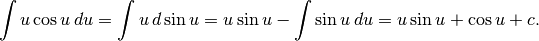
Poiché 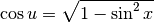 è positiva, perché la funzione inversa
del seno esiste in un’intervallo nel quale il coseno è positivo, possiamo
scrivere:
è positiva, perché la funzione inversa
del seno esiste in un’intervallo nel quale il coseno è positivo, possiamo
scrivere: 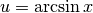 ,
, 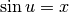 ,
, 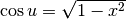 ,
da cui
,
da cui
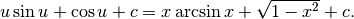
 ¶
¶
Integriamo prima per parti, poi operiamo una sostituzione.
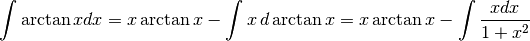
Ora poniamo 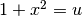 , quindi
, quindi 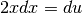 e
e 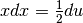 .
.
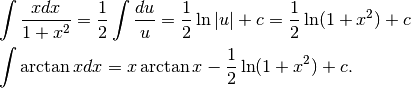
Negli esercizi di fine capitolo è richiesta l’integrazione per sostituzione e per parti. Ovviamente il risultato sarà uguale.
E ora la regola¶
Negli esempi precedenti, sembra evidente che integrare le funzioni inverse
comporti una procedura con alcuni passi inevitabili. Quando abbiamo integrato
prima per parti e poi per sostituzione, per calcolare 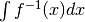 abbiamo dovuto calcolare
abbiamo dovuto calcolare 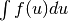 , cioè per integrare
la funzione inversa siamo passati per l’integrale della funzione diretta.
Infatti:
, cioè per integrare
la funzione inversa siamo passati per l’integrale della funzione diretta.
Infatti:
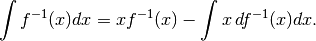
Sostituendo con 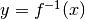 si ha
si ha 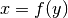 e per il secondo
integrale vale:
e per il secondo
integrale vale:
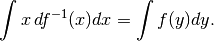
Quindi
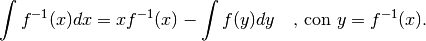
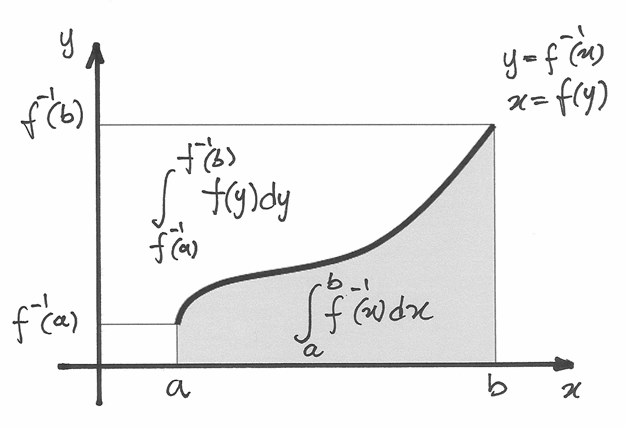
Una rappresentazione geometrica¶
Possiamo leggere il significato dell’ultima formula utilizzando il teorema fondamentale del calcolo integrale:
![\int_a^b f^{-1}(x)dx=\left[xf^{-1}(x)\right]_a^b-\int_{f^{-1}(a)}^{f^{-1}(b)} f(y)dy](../../../_images/math/f0c3d3242f3c4c704adb92317f44cfab450ca0b8.png)
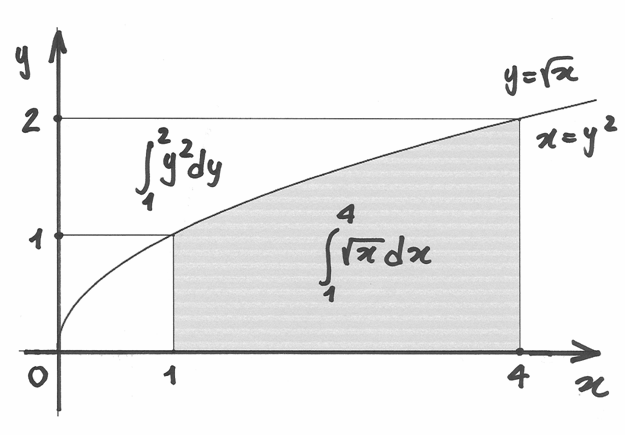
Immaginiamo, per esempio, di non conoscere la primitiva di 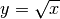 e di dovere calcolare
e di dovere calcolare 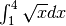 .
.
L’area richiesta è in evidenza nel disegno e si ricava per sottrazione: dal
rettangolo di base 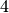 e altezza
e altezza 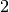 si sottrae il quadrato di lato
si sottrae il quadrato di lato
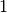 e anche l’area contrassegnata con
e anche l’area contrassegnata con 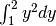 .
.
![\int_1^4\sqrt{x}dx=&4\times 2- 1\times 1-\int_1^2 y^2dy=
8-1-\left[\frac{y^3}{3}\right]_1^4=8-1-\frac{7}{3}=\frac{14}{3}.\\
=&\left[x\sqrt{x}\right]_1^4-\int_{\sqrt{1}}^{\sqrt{4}}y^2 dy=
\left[ x^\frac{3}{2}\right]_1^4-\int_1^2 y^2 dy.](../../../_images/math/2ebf5a46b363aca40af751e6b6b24e0066bc5ec1.png)
Confrontiamo questo calcolo con quello che effettivamente eseguiamo, conoscendo la primitiva:
Generalizziamo l’esempio e riportiamoci al caso di una funzione qualsiasi.
L’integrale definito dell’inversa di una funzione di cui si conosce l’integrale
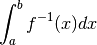
ha il significato geometrico dell’area che si ottiene sottraendo dall’area
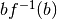 (del rettangolo di lati
(del rettangolo di lati 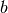 e
e 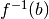 ) l’area
) l’area
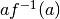 (del rettangolo di lati
(del rettangolo di lati  e
e 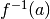 ) e
l’area data da
) e
l’area data da 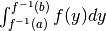 .
.
Note
Non serve imparare a memoria questa formula: abbiamo visto che si è obbligati ad usarla quando si integra prima per parti e poi con una sostituzione.
Riassunto¶
- Riassumiamo gli integrali notevoli, immediati e non, calcolati fin qui, comprendendo quelli del capitolo precedente.
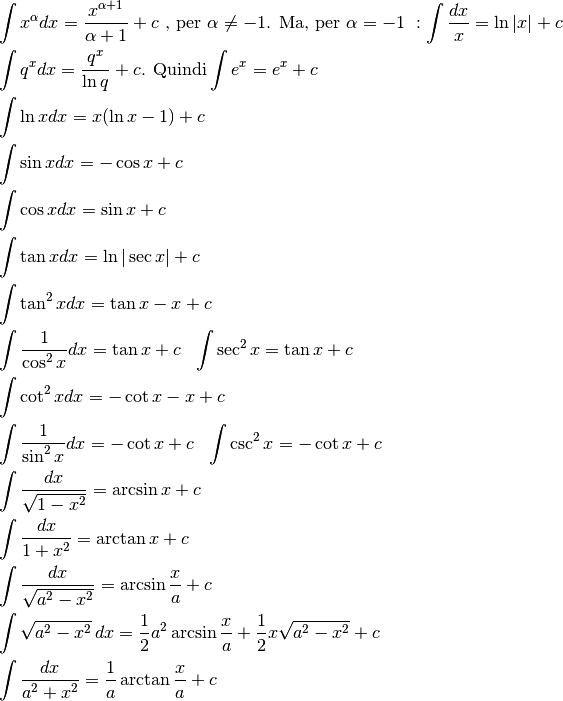
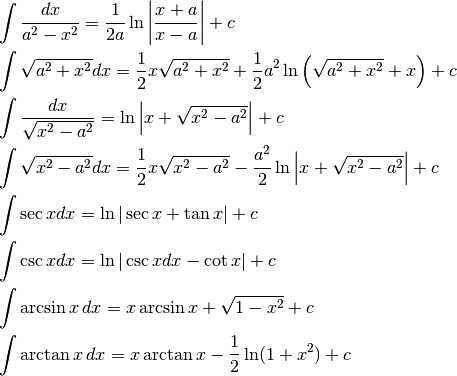
- L’integrale di una funzione inversa segue la formula:
![\int_a^b f^{-1}(x)dx=\left[xf^{-1}(x)\right]_a^b-\int_{f^{-1}(a)}^{f^{-1}(b)} f(y)dy](../../../_images/math/f0c3d3242f3c4c704adb92317f44cfab450ca0b8.png)
Esercizi¶
- Calcola:
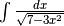
- Calcola:
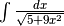
- Calcola:
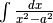
- Integrando, dimostra che
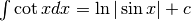 .
. - Risolvi l’es.7.1.9 riscrivendo la frazione integranda come differenza di due frazioni.
- Calcola:
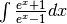 .
. - Risolvi l’es.7.2.2 integrando prima per sostituzione e poi per parti.
- Calcola
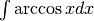 .
. - Verifica, derivando, tutti i risultati degli integrali notevoli elencati nel Riassunto.
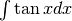
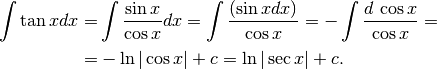
![\int_1^4\sqrt{x}dx=\int_1^4 x^{\frac{1}{2}}dx=\left[\frac{2}{3}x^{\frac{3}{2}} \right]_1^4=
\frac{2}{3}\left(4^{\frac{3}{2}}-1^{\frac{3}{2}} \right)= \frac{2}{3}(8-1)=
(8-1)-\frac{8-1}{3}=\frac{14}{3}.](../../../_images/math/45f723bf47a838653b92ac96997ddc135046c5ff.png)