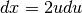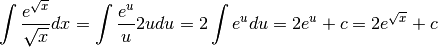L’integrale indefinito¶
La ricerca di un metodo per trovare le primitive di una funzione è arrivata al punto decisivo: pensare una primitiva come inversa di una derivata è un metodo potente, molto di più che pensarla come somma infinita di incrementi infinitesimi, a partire da un valore iniziale. Un se condo vantaggio è poi che, grazie al Teorema fondamentale, gli integrali definiti si calcolano più facilmente.
La notazione per la primitiva¶
Se 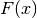 è una primitiva allora
è una primitiva allora 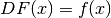 . Si può quindi
usare, almeno provvisoriamente, il simbolo
. Si può quindi
usare, almeno provvisoriamente, il simbolo 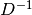 per indicare
il calcolo della primitiva.
per indicare
il calcolo della primitiva.
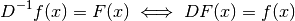
Con questo simbolo possiamo esprimere facilmente la linearità di 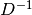 ,
che consegue dalla linearità di
,
che consegue dalla linearità di 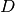 . In pratica devono valere le due condizioni
. In pratica devono valere le due condizioni
![D^{-1}[f(x)+ g(x)]=D^{-1}&f(x)+D^{-1}g(x)=F(x)+G(x) \\
D^{-1}[kf(x)]&=kD^{-1}f(x)=kF(x)](../../../_images/math/17a5f93eed6a5f5ab2908b730551cedacaf325ed.png)
Note
Ricordiamo che la linearità si esprime attraverso l’operazione di somma e
di prodotto per una costante. Una funzione è lineare se
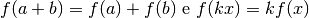 come avviene appunto per le funzioni il cui grafico è una retta per l’origine.
come avviene appunto per le funzioni il cui grafico è una retta per l’origine.
Per tutto quanto visto finora, fra le due operazioni valgono anche:
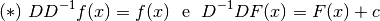
cioè la derivazione e la ricerca delle primitive non sono
esattamente l’una il contrario dell’altra, perché la costante  ,
rende l’applicazione dei due operatori non commutativa.
,
rende l’applicazione dei due operatori non commutativa.
La parte sostanziale dei calcoli nella ricerca della primitiva è l’integrale.
Nel caso discreto abbiamo indicato una generica primitiva con il simbolo della
somma senza indici, perché le sue proprietà sono quelle della somma e il suo
valore si esprime attraverso la somma. Seguendo lo stesso filo logico, diamo
al simbolo 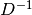 , nel caso continuo, il contenuto legato alla sostanza
del calcolo:
, nel caso continuo, il contenuto legato alla sostanza
del calcolo: 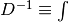 , cioè al segno di integrazione, senza
indici.
, cioè al segno di integrazione, senza
indici.
Le proprietà dell’integrale discendono dalle proprietà della somma. Per esempio, a proposito della linearità, si ricava che, dati
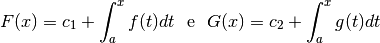
vale
![&F(x)+G(x)=\left(c_1+\int_a^xf(t)dt\right)+\left(c_2+\int_a^xg(t)dt\right)=\\
&=(c_1+c_2)+\int_a^x[f(t)+g(t)]dt=c+\int_a^x[f(t)+g(t)]dt](../../../_images/math/8ba082fa4b810c003bb5a421223bdcbf90ae5f69.png)
Per cui la somma di due primitive è la primitiva della somma. Ma vale anche il contrario, infatti:
![c+\int_a^x[f(t)+g(t)]dt=c+\int_a^xf(t)dt+\int_a^xg(t)dt](../../../_images/math/f66e3c0bff12dbc4073c5c1ef6311d19cae1e178.png)
e quindi è vero che ![D^{-1}[f(x)+ g(x)]=D^{-1}f(x)+D^{-1}g(x)](../../../_images/math/f8d319f22dc71d2ee059b175e9d1e5420ee868bb.png) . In modo
analogo si dimostra (vedi Esercizi) che
. In modo
analogo si dimostra (vedi Esercizi) che
![D^{-1}[kf(x)]=kD^{-1}f(x)](../../../_images/math/c41627a1869009e500c04a8a36266ff61ed9ab45.png)
Con l’integrale indefinito possiamo facilmente verificare le proprietà 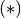 .
Infatti
.
Infatti

L’integrale indefinito¶
In conclusione, indichiamo una generica primitiva della funzione  con
con
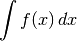
che chiameremo integrale indefinito della funzione 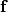 .
.
Non si tratta solo di eliminare degli indici e rendere più agile la notazione: l’integrale definito è un numero, quello indefinito è l’espressione di una generica primitiva. Il legame fra i due è il Teorema fondamentale.
Le formule sulla linearità si traducono quindi in queste due righe:
![&\int[f(x)\pm g(x)]dx=\int f(x)dx \pm \int g(x)dx\\
&\int kf(x)dx=k\int f(x)dx](../../../_images/math/e7dffca9aed8a9f683893dfbf7de3422e0dd59fd.png)
È facile inoltre verificare che
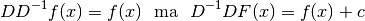
e lo lasciamo per esercizio.
Integrali immediati¶
Rivediamo con la nuova notazione alcuni calcoli già svolti nel capitolo precedente e aggiungiamo i ragionamenti utili a cercare le generiche primitive di altre funzioni notevoli. Questi casi, che sono tipici e per questo si utilizzano in esercizi più complessi, si dicono integrali immediati.
Integrare 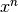 ¶
¶
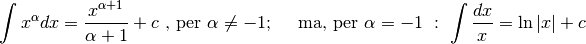
Integrare le funzioni circolari¶
Per la dimostrazione delle prossime due formule facciamo riferimento al Cap.5.
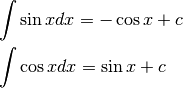
A proposito della tangente, da 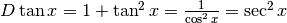 ,
ricaviamo:
,
ricaviamo:
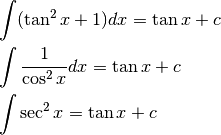
Il primo integrale è utile solo in quanto ![D[\tan x-x]= 1+ \tan^2x -1= \tan^2 x](../../../_images/math/28e188ae93b8e3ef93208217a1a5fe2243792cfe.png) ,
per cui:
,
per cui:
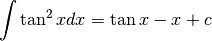
Per la cotangente si procede in modo analogo e si ricava:
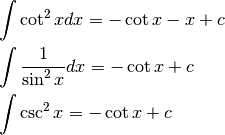
Da 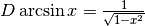 e da
e da 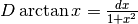 ricaviamo
ricaviamo
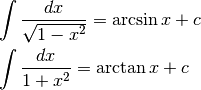
Integrale definito e integrale indefinito¶
Ricordando come è stato fatto per le successioni, adottiamo una notazione più
sintetica per rappresentare la differenza 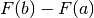 :
:
![F(b)-F(a)=\left[F(x)\right]_a^b](../../../_images/math/47b849fbca3960ea508173fd98910988baf20b96.png)
e riscriviamo in questo modo il Teorema fondamentale:
![\int_a^bf(x)dx=\left[F(x)\right]_a^b](../../../_images/math/4158a2f00cf2aa7bc07f86e55049f208a883ef70.png)
che significa:
![\int_a^bf(x)dx=\left[\int f(x)dx)\right]_a^b](../../../_images/math/019f4f1be97564897efd6ef84a8cbf06085e2704.png)
L’ultimo termine indica la regola e la precedenza nelle operazioni: per calcolare un integrale definito si calcola prima l’integrale indefinito, cioè una generica primitiva della funzione integranda, e poi si fa la differenza fra i valori di una primitiva negli estremi di integrazione. Per esempio:
![&\int_0^\frac{\pi}{2}(3x+5\sin x)dx=\left[3\int xdx+5\int\sin x dx\right]_0^\frac{\pi}{2}=
\left[3\frac{x^2}{2}+5(-\cos x) +c\right]_0^\frac{\pi}{2}=\\
&=\left[\frac{3}{2}x^2-5\cos x +c\right]_0^\frac{\pi}{2}=
\left[\frac{3}{2}\left(\frac{\pi}{2}\right)^2-5\cos \frac{\pi}{2} +c\right]-[0-5\cos 0+ c]=\frac{3\pi^2}{8}+5.](../../../_images/math/08a5f1b9e1edac78acfbbd0b437a55f48fdd31ba.png)
In realtà nello svolgimento si può tralasciare la costante  , perchè
viene comunque eliminata dalla differenza. Applichiamo anche queste ultime
nozioni nei prossimi esercizi.
, perchè
viene comunque eliminata dalla differenza. Applichiamo anche queste ultime
nozioni nei prossimi esercizi.
Esercizi svolti¶
Calcola l’integrale definito di una funzione esponenziale.¶
![\int_a^bq^xdx=\left[\frac {q^x}{\ln q}\right]_a^b=\frac{q^b-q^a}{\ln q}`](../../../_images/math/1e829178f6df20d63818b16468a21e693e150110.png)
Calcola 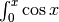 e visualizza il suo significato geometrico.¶
e visualizza il suo significato geometrico.¶
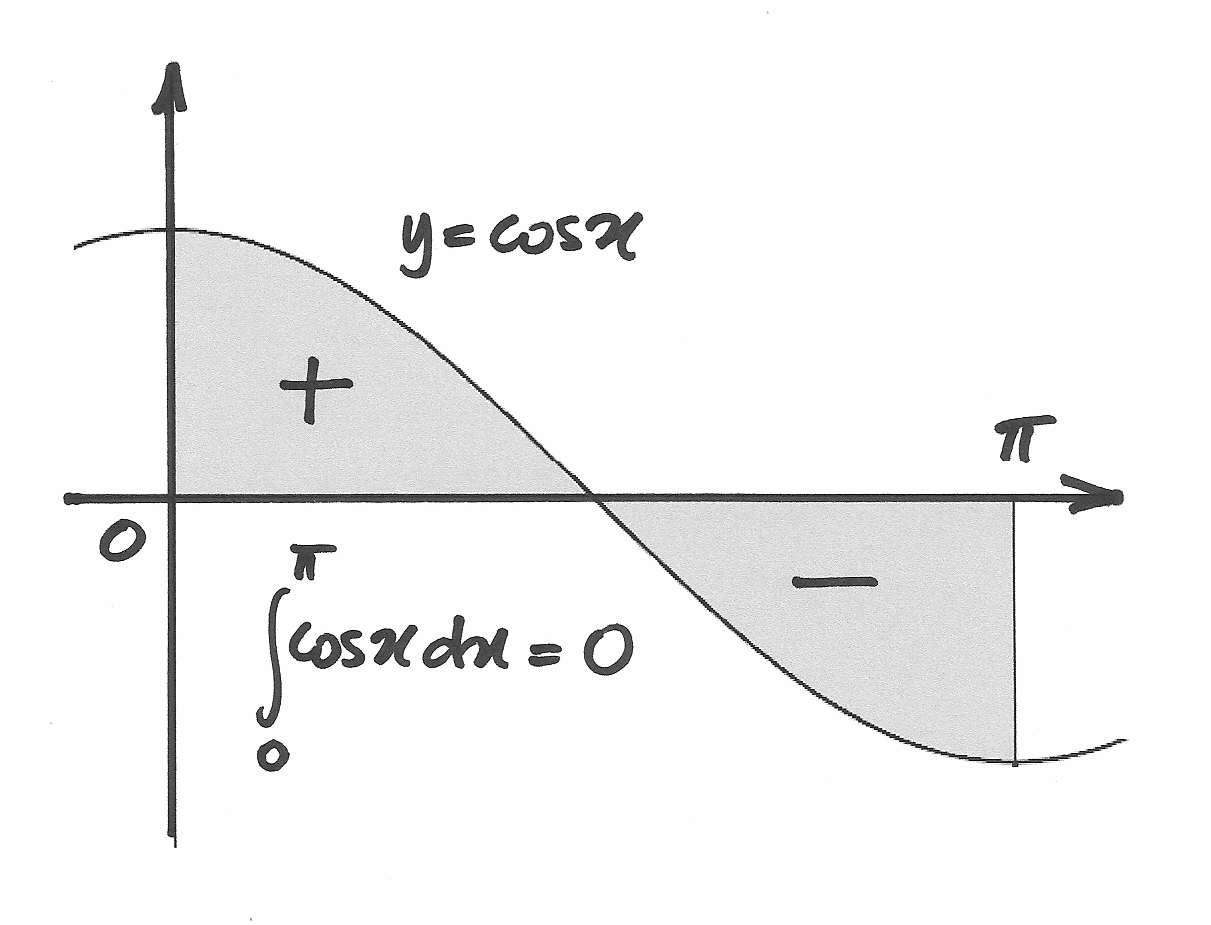
![\int_0^\pi\cos x=\left[\sin x +c\right]_0^\pi=\sin \pi-\sin 0=0](../../../_images/math/6cb206b444423214fc641f7cd0d526f2405a6906.png)
Il fatto che il risultato sia nullo poteva essere previsto da considerazioni di simmetria: nell’intervallo considerato l’area sottesa alla curva è per metà positiva e per metà negativa.
Calcola 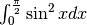 .¶
.¶
b) una soluzione sbagliata¶
Si potrebbe pensare: visto che 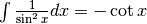 allora
allora
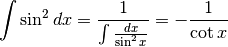
Purtroppo, il principio che la primitiva della reciproca di una funzione sia la
reciproca della primitiva è sbagliato. Confronta per esempio 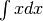 e
e 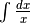 . D’altra parte questa ipotesi non vale neanche nel
calcolo delle somme: la somma dei reciproci non è il reciproco della somma.
. D’altra parte questa ipotesi non vale neanche nel
calcolo delle somme: la somma dei reciproci non è il reciproco della somma.
c) la soluzione elegante¶
Nell’intervallo ![[0,\frac{\pi}{2}]](../../../_images/math/4dbe0601d7c7db8b873cdac7e69beeb2b234c186.png) il seno e il coseno assumono gli stessi
valori, anche se nell’ordine inverso. Lo stesso avviene per i loro quadrati, per cui
il seno e il coseno assumono gli stessi
valori, anche se nell’ordine inverso. Lo stesso avviene per i loro quadrati, per cui
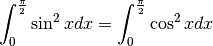
e quindi la loro somma fa il doppio del numero cercato.
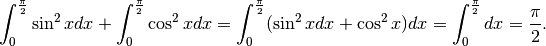
Essendo questo il doppio del numero cercato, è facile avere il risultato corretto.
Note
Le considerazioni sulla simmetria della funzione e delle aree sottese al suo grafico sono di grande aiuto nell’evitare i calcoli. Tuttavia non sempre sono possibili. In questo esercizio, per esempio, sarebbe bastato dover svolgere l’integrale su un intervallo diverso per rendere non applicabili questi ultimi ragionamenti.
Sostituire la variabile¶
Nella soluzione diretta dell’ultimo esercizio si utilizza 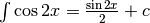 .
La correttezza dell’uguaglianza è semplice da verificare: basta derivare il suo
secondo membro. Ma ragioniamo sulla tecnica che abbiamo applicato, in modo che ci
sia utile anche in casi più difficili.
.
La correttezza dell’uguaglianza è semplice da verificare: basta derivare il suo
secondo membro. Ma ragioniamo sulla tecnica che abbiamo applicato, in modo che ci
sia utile anche in casi più difficili.
Il ragionamento sottinteso è:  e
e
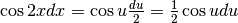 .
Quindi
.
Quindi 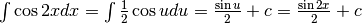 .
.
In realtà scrivere questi dettagli nei casi semplici diventa ben presto superfluo
dopo i primi esercizi, ma ora è giusto mettere in evidenza ogni cosa.
Per esempio, se si dovesse calcolare 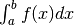 e si rendesse necessaria
un’analoga sostituzione di variabile, il ragionamento sarebbe:
e si rendesse necessaria
un’analoga sostituzione di variabile, il ragionamento sarebbe:
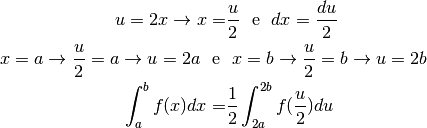
Il cambio di variabile nell’ultimo integrale trova spiegazione nel disegno.
L’asse verticale inferiore è l’asse degli 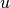 , dove gli intervallini
infinitesimi
, dove gli intervallini
infinitesimi 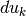 corrispondono agli intervallini infinitesimi dimezzati
corrispondono agli intervallini infinitesimi dimezzati 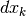 attraverso la relazione
attraverso la relazione 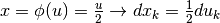 .
Così, facendo uso della rappresentazione originale dell’integrale definito, la
trasformazione diventa:
.
Così, facendo uso della rappresentazione originale dell’integrale definito, la
trasformazione diventa:
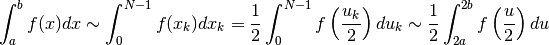
Come abbiamo già detto, in casi semplici come questo tutta la rappresentazione può
essere superflua. È però necessario ricordare che la trasformazione del differenziale
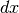 nel differenziale
nel differenziale 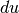 dipende dalla funzione matematica desiderata.
Nel caso in esame si è preferito che gli intervalli sull’asse
dipende dalla funzione matematica desiderata.
Nel caso in esame si è preferito che gli intervalli sull’asse 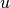 siano doppi
dei corrispondenti intervalli sull’asse
siano doppi
dei corrispondenti intervalli sull’asse  , quindi si tratta di un rapporto
costante. Ma di solito è necessaria una dipendenza diversa e variabile.
, quindi si tratta di un rapporto
costante. Ma di solito è necessaria una dipendenza diversa e variabile.
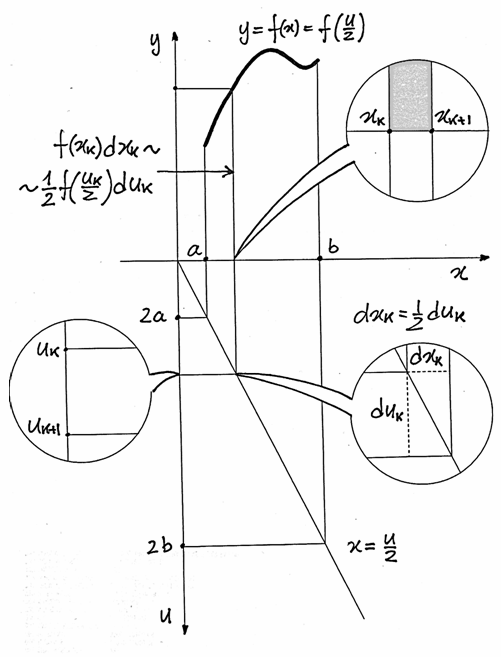
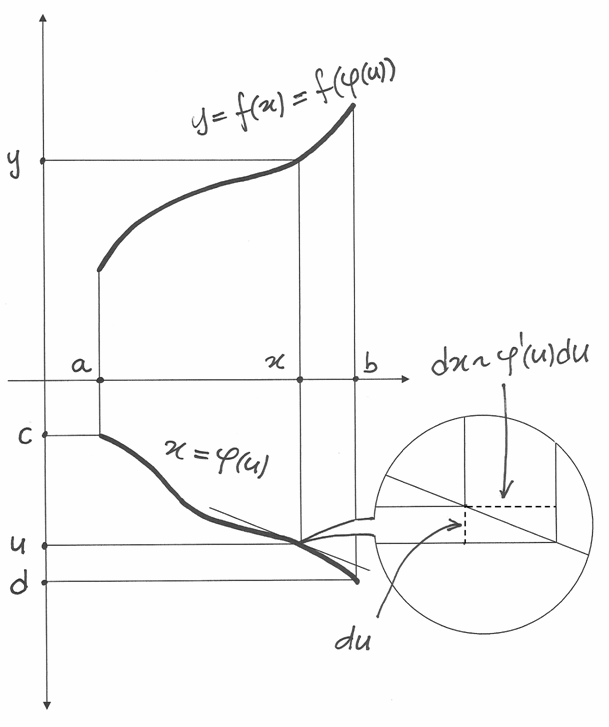
Se quindi utilizziamo una funzione di trasformazione che chiamiamo genericamente
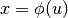 , con
, con ![x\in [a,b]](../../../_images/math/cb9ed72f8db4b1233bb65701d2fc295ba6138b74.png) e
e ![u\in [c,d]](../../../_images/math/332ef1f272e4799e5839f82b78e1df15e631ec22.png) , avremo
, avremo
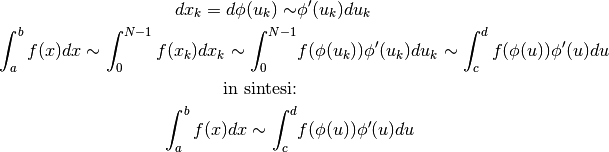
Anche gli estremi degli intervalli seguono la regola di trasformazione:
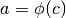 e
e 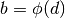 . Il problema è che però se
. Il problema è che però se 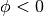 ,
cioè se la funzione di trasformazione è decrescente, l’integrale precedente
ha segno opposto rispetto a quando la funzione è crescente:
,
cioè se la funzione di trasformazione è decrescente, l’integrale precedente
ha segno opposto rispetto a quando la funzione è crescente:
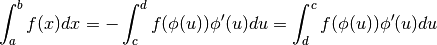
In questa formula 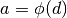 e
e 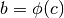 . In pratica, se
. In pratica, se 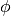 è crescente
è crescente 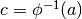 e
e 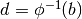 , mentre, se è
decrescente,
, mentre, se è
decrescente, 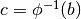 e
e 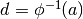
Quindi vale in ogni caso la formula seguente, detta formula di sostituzione per gli integrali definiti:
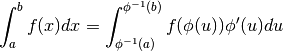
Questa invece è l’equivalente formula per l’integrale indefinito:
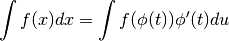
Esercizi svolti con sostituzione¶
Calcola 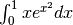 ¶
¶
Poniamo 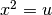 . Ne consegue
. Ne consegue
![&x=\sqrt{u}\ \mbox{, }\ dx=\frac{1}{2\sqrt{u}}.\ \mbox{ Per }x=0\to u=0^2=0;\ \mbox{ Per }x=1\to u=1^2=1\\
&\int_0^1 xe^{x^2}dx=\int_0^1\sqrt{u}e^u\frac{du}{2\sqrt{u}}=\frac{1}{2}\int_0^1e^udu
=\frac{1}{2}\left[e^u\right]_0^1=\frac{e-1}{2}.](../../../_images/math/afffbf90b393e38f5713d283aee1ca0f6e8ca285.png)
Un altro modo, equivalente, è quello di cercare prima la primitiva e poi applicarla all’integrale definito:
![&\int xe^{x^2}dx=\int\sqrt{u}e^u\frac{du}{2\sqrt{u}}=\frac{1}{2}\int e^udu=\frac{1}{2}e^u+c=
\frac{1}{2}e^{x^2}+c\\
&\int_0^1 xe^{x^2}dx=\left[\frac{1}{2}e^{x^2} \right]_0^1 =\frac{1}{2}e-\frac{1}{2}=\frac{e-1}{2}](../../../_images/math/4132d1febefe959c64ef8e98fb8fdde464c9090f.png)
Calcola 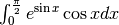 ¶
¶
Si pone 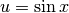 , da cui deriva che
, da cui deriva che
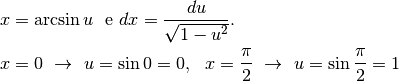
Dato che abbiamo scelto di sostituire il seno, occorre trasformare il coseno
in modo da usare la sostituzione, cioè  .
Teniamo il segno positivo perchè il seno si inverte nell’intervallo
.
Teniamo il segno positivo perchè il seno si inverte nell’intervallo ![[-\frac{\pi}{2},\frac{\pi}{2}]](../../../_images/math/a9f15de39a1357d19d371a10d56e1d2eccf3c114.png) ,
dove il coseno è positivo. Quindi:
,
dove il coseno è positivo. Quindi:
![\int_0^{\frac{\pi}{2}}e^{\sin x}\cos xdx=\int_0^1 e^u\sqrt{1-u^2}\frac{du}{\sqrt{1-u^2}}=
\int_0^1e^udu=\left[e^u \right]_0^1=e-1.](../../../_images/math/916131355c57ef6191bed86e4016fc3df6840889.png)
Note
Come vedremo più avanti, l’esercizio si risolve anche senza sostituire il
coseno. Basta rilevare che 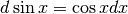 per cui
per cui
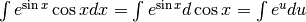 .
.
Integrare per parti¶
Iniziamo da un esempio: calcolare 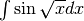 . Poniamo
. Poniamo 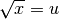 e
e
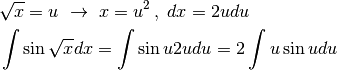
Sappiamo già, dalle somme, che non esiste una regola semplice per
l’integrale di un prodotto: in particolare 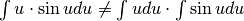 .
.
Ricorriamo ai differenziali noti: 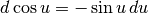 , perciò
, perciò
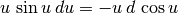 . L’obiettivo era ottenere
. L’obiettivo era ottenere 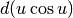 ,
molto più facile da integrare, perché
,
molto più facile da integrare, perché 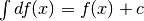 . Vediamo di
quanto ci siamo avvicinati:
. Vediamo di
quanto ci siamo avvicinati:
![&d(u\cos u)=du\cos u+ud\cos u \mbox{, e quindi:}\\
&ud\cos u=d(u\cos u)-du\cos u .\\
&2\int u\sin u du=-2\int u\,d\,\cos u=-2\int[\d(u\cos u)-du\cos u]=\\
&=-2\int\d(u\cos u)+2\int\cos u du=-2u\cos u+2\sin u +c](../../../_images/math/ed1e49efb1c8fc46589956f5d77da57457572f02.png)
Concludiamo che
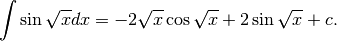
La tecnica illustrata nell’esempio si chiama dell’integrazione indefinita per parti, che ora descriviamo in modo più formale:
- Ci è richiesto l’integrale di un prodotto
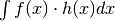
- Nel prodotto individuiamo una parte infinitesima:
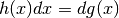 .
Questo è possibile se conosciamo una primitiva
.
Questo è possibile se conosciamo una primitiva 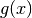 di
di 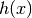 .
. - Applichiamo la formula:
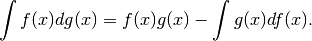
 e
e 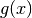 si chiamano parti finite, mentre
si chiamano parti finite, mentre 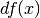 e
e 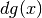 si chiamano parti infinitesime.
si chiamano parti infinitesime.
La formula dice che l’integrale di una parte finita per una infinitesima è uguale al prodotto delle parti finite meno l’integrale delle parti scambiate fra loro.
La ragione della formula, come si è visto nell’esempio, è :
![d[f(x)g(x)]=& df(x)g(x)+f(x)dg(x)\\
f(x)dg(x)=& d[f(x)g(x)]-df(x)g(x)\\
\int f(x)\cdot h(x)dx=\int f(x)dg(x)=&\int d[f(x)g(x)]-\int g(x)df(x)=\\
=f(x)g(x)-&\int g(x)df(x).](../../../_images/math/f0601e0b4fcd3ee00afbd77c34029b7cd1185463.png)
Nell’uso della formula, i punti importanti sono due: si deve essere in grado di
trovare la primitiva 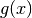 e l’ultimo integrale deve essere calcolabile
direttamente.
Come vedremo nei prossimi esempi, però, talora si può porre rimedio alla mancanza
di quest’ultima condizione.
e l’ultimo integrale deve essere calcolabile
direttamente.
Come vedremo nei prossimi esempi, però, talora si può porre rimedio alla mancanza
di quest’ultima condizione.
Esempi¶
 ¶
¶
Gli integrali del tipo 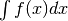 possono essere trattati per parti. Allora
applicare la formula è particolarmente semplice.
possono essere trattati per parti. Allora
applicare la formula è particolarmente semplice.  sarà la parte finita
relativa a
sarà la parte finita
relativa a 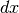 .
.
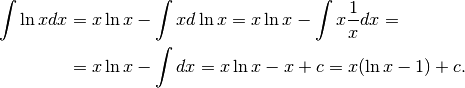
Derivando, è facile verificare la correttezza del risultato.
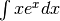 ¶
¶
Qui abbiamo effettivamente un prodotto fra due funzioni e dobbiamo scegliere
la parte infinitesima: può essere 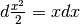 oppure
oppure 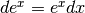 .
Nel primo caso abbiamo:
.
Nel primo caso abbiamo:
![\int e^xxdx=\int e^xd\frac{x^2}{2}=\frac{1}{2}\int e^x dx^2=
\frac{1}{2}\left[x^2e^x-\int x^2de^x \right]=\frac{1}{2}\left[x^2e^x-\int x^2e^xdx \right]](../../../_images/math/fca8575796627efd54d8742891a3757f9dcb3ad5.png)
Dato che l’ultimo integrale è peggiore del primo, non abbiamo ottenuto vantaggi. Proviamo la seconda scelta.
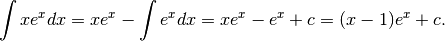
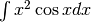 ¶
¶
In questo integrale, l’integrazione per parti non porta direttamente alla soluzione, ma semplifica l’esercizio, che viene completato con una seconda integrazione per parti.
Scartiamo senz’altro la scelta di 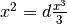 come parte infinitesima:
abbiamo già visto nell’esempio precedente che non migliora la situazione.
Non resta che
come parte infinitesima:
abbiamo già visto nell’esempio precedente che non migliora la situazione.
Non resta che 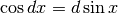 .
.
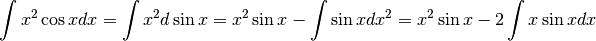
L’ultimo integrale non è facile, ma è migliore del primo. Lo risolviamo per parti.
![\int x\sin xdx=\int xd(-\cos x)=-\int xd\cos x=-\left[x\cos x-\int \cos x dx \right]
=-x\cos x+\sin x +c.](../../../_images/math/500c615867d66bb35cd3f7226d20fabfa94e57b7.png)
Quindi:
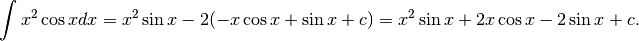
Il risultato si può verificare derivando.
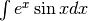 ¶
¶
Scegliamo la parte infinitesima: 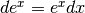 .
.
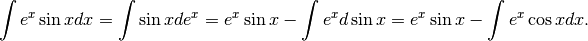
Insistiamo, calcolando per parti l’ultimo integrale.
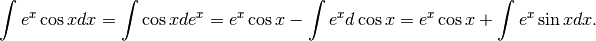
Abbiamo ottenuto:
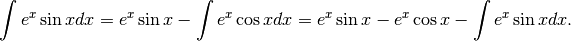
Ora possiamo risolvere:
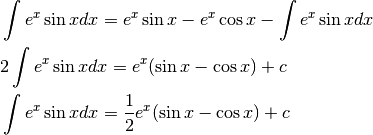
In quest’ultimo esempio il metodo dell’integrazione per parti, anche se ripetuto, non porta alla soluzione in modo diretto. Infatti non semplifica l’esercizio, anzi lo ripropone uguale in una sua parte. Questo porta ad un’equazione e, risolvendola, si ottiene il risultato.
La costante  ¶
¶
Come già sappiamo, la costante  rappresenta gli infiniti valori
possibili che distinguono una dall’altra le primitive della funzione data.
rappresenta gli infiniti valori
possibili che distinguono una dall’altra le primitive della funzione data.
 è parte di ogni integrale indefinito e per
questo si aggiunge al termine del calcolo. Nell’ultimo esempio,
è parte di ogni integrale indefinito e per
questo si aggiunge al termine del calcolo. Nell’ultimo esempio,  compare nelle due ultime righe e rappresenta in realtà due costanti diverse,
che dovrebbero essere espresse da
compare nelle due ultime righe e rappresenta in realtà due costanti diverse,
che dovrebbero essere espresse da  e da
e da 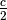 . Ma, in
questo caso come in tutti i precedenti, non abbiamo distinto i nomi delle
costanti perché entrambe coprono lo stesso arco di valori, dovendo variare
infinitamente.
. Ma, in
questo caso come in tutti i precedenti, non abbiamo distinto i nomi delle
costanti perché entrambe coprono lo stesso arco di valori, dovendo variare
infinitamente.
Il segno di integrale indefinito 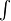 corrisponde alla richiesta:
“Trova tutte le possibili primitive” e quindi prevede già la somma
corrisponde alla richiesta:
“Trova tutte le possibili primitive” e quindi prevede già la somma 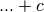 inglobata al suo interno.
Infatti si scrive
inglobata al suo interno.
Infatti si scrive 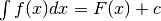 . Il fatto che
. Il fatto che  rappresenti
una variazione infinita e non un numero si può capire dagli esempi seguenti.
rappresenti
una variazione infinita e non un numero si può capire dagli esempi seguenti.
- Calcoliamo in due modi diversi
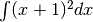 .
.
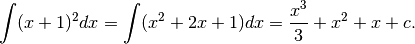
invece, ponendo 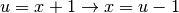 e
e 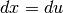 , abbiamo
, abbiamo
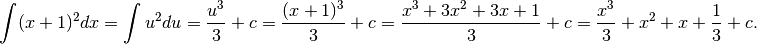
Sono due primitive che differiscono per  , ma si equivalgono.
Infatti, basta pensare che
, ma si equivalgono.
Infatti, basta pensare che  del primo risultato, nel suo variare, assume
valori di
del primo risultato, nel suo variare, assume
valori di  più grandi rispetto a quelli che assume nel secondo
risultato.
più grandi rispetto a quelli che assume nel secondo
risultato.
- Calcoliamo per parti
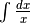 .
.
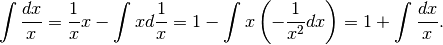
Abbiamo un paradosso: 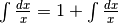 . Se considerassimo
i due integrali come numeri, sarebbe lecito eliminarli dall’uguaglianza e
resterebbe l’assurdo
. Se considerassimo
i due integrali come numeri, sarebbe lecito eliminarli dall’uguaglianza e
resterebbe l’assurdo 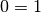 . Ma si tratta invece di due insiemi infiniti
di primitive, che in sè contengono due costanti di volta in volta diverse per
una unità.
. Ma si tratta invece di due insiemi infiniti
di primitive, che in sè contengono due costanti di volta in volta diverse per
una unità.
Ancora qualche dettaglio su  . Ricaviamo di nuovo la formula
dell’integrazione per parti.
. Ricaviamo di nuovo la formula
dell’integrazione per parti.
![&[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x) \mbox{, quindi, integrando:}\\
&\int[f'(x)g(x)+f(x)g'(x)]dx=f(x)g(x)+c\\
&\int f'(x)g(x)dx + \int f(x)g'(x)dx=f(x)g(x)+c\\
&\int f'(x)g(x)dx= f(x)g(x)- \int f(x)g'(x)dx](../../../_images/math/ab24cd6c7816de8d4e594f5925cfbc4446de1d5d.png)
Nell’ultimo passaggio  è sparita perchè inglobata nell’integrale a destra.
Invece nel secondo passaggio la costante è comparsa perchè a sinistra si
chiede, con l’integrazione, di ricavare tutte le possibili primitive.
è sparita perchè inglobata nell’integrale a destra.
Invece nel secondo passaggio la costante è comparsa perchè a sinistra si
chiede, con l’integrazione, di ricavare tutte le possibili primitive.
Note
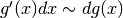 e
e 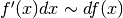 . Per questo, la
formula appena ricavata corrisponde alle regola dell’integrazione per parti
illustrata in precedenza.
. Per questo, la
formula appena ricavata corrisponde alle regola dell’integrazione per parti
illustrata in precedenza.
L’area nell’integrazione per parti¶
Il teorema fondamentale si applica anche all’integrale per parti, ottenendo il risultato che segue:
![&\int_a^b[f'(x)g(x)+f(x)g'(x)]dx=[f(x)g(x)]_a^b\\
&\int_a^b f'(x)g(x)dx+ \int_a^bf(x)g'(x)dx=[f(x)g(x)]_a^b\\
&\int_a^bf(x)g'(x)dx=[f(x)g(x)]_a^b- \int_a^b f'(x)g(x)dx](../../../_images/math/63a25ac508659e13279600a0eb3b37f579b342cd.png)
L’ultima uguaglianza è analoga a :
![\int_a^bf(x)dg(x)=[f(x)g(x)]_a^b- \int_a^b g(x)df(x)](../../../_images/math/0a19b2672c81ac8f4c2965e07e9594126acccd0e.png)
ed è la formula di integrazione definita per parti.
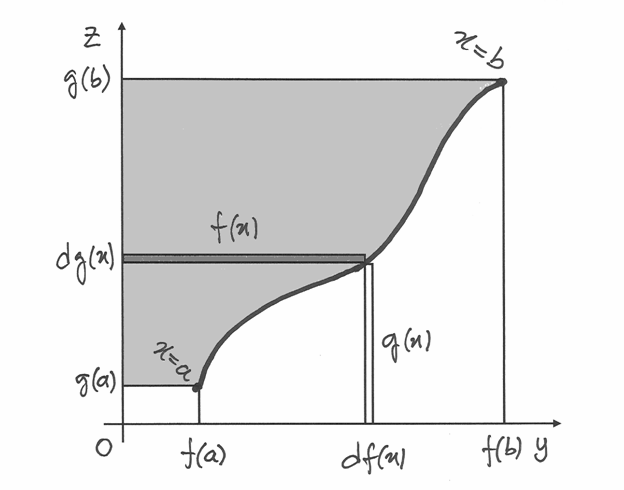
Possiamo immaginare una rappresentazione geometrica di questa formula, almeno
nel caso di funzioni con valori positivi e differenziali positivi.
Possiamo immaginare che i valori di  siano in ascissa e crescano
verso destra e lo stesso avvenga per i valori di
siano in ascissa e crescano
verso destra e lo stesso avvenga per i valori di 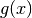 sulle ordinate,
crescenti verso l’alto. Le coppie
sulle ordinate,
crescenti verso l’alto. Le coppie 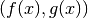 sono i punti del piano
che tracciano la curva che, al variare di
sono i punti del piano
che tracciano la curva che, al variare di  , va da
, va da 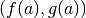 a
a 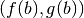 . È la curva di equazioni parametriche
. È la curva di equazioni parametriche
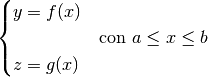
L’area in evidenza corrisponde a 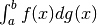 ,
formata dalle strisce indistinguibili dai rettangoli di base
,
formata dalle strisce indistinguibili dai rettangoli di base  e altezza
infinitesima
e altezza
infinitesima 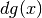 . Ma la stessa area si ottiene dall’intero rettangolo
(di area
. Ma la stessa area si ottiene dall’intero rettangolo
(di area 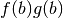 ) sottraendo due parti: il piccolo rettangolo vicino
all’origine (area
) sottraendo due parti: il piccolo rettangolo vicino
all’origine (area 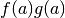 ) e l’integrale delle strisce verticali
indistinguibili dai rettangoli di base infinitesima
) e l’integrale delle strisce verticali
indistinguibili dai rettangoli di base infinitesima 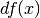 e altezza
e altezza
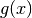 .
.
Quindi:
![&\int_a^bf(x)dg(x)=f(b)g(b)-f(a)g(a) - \int_a^b g(x)df(x)\\
&\mbox {e infine}\\
&\int_a^bf(x)dg(x)=[f(x)g(x)]_a^b- \int_a^b g(x)df(x)](../../../_images/math/a7dc21e56766df1ae31dcd0b23b5d9344fbe306b.png)
Riassunto¶
- La primitiva conserva la linearità: la primitiva di una somma è la somma delle primitive e la primitiva di una funzione moltiplicata per una costante è anch’essa moltiplicata dalla stessa costante.
- La primitiva non è esattamente l’operazione inversa della derivata, perché derivare la primitiva di una funzione non è come cercare la primitiva della derivata di una funzione.
- Il simbolo
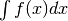 è detto integrale indefinito di
è detto integrale indefinito di  e
rappresenta le primitive
e
rappresenta le primitive 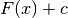 . L’integrale si calcola pensando
. L’integrale si calcola pensando
 come derivata della funzione incognita.
come derivata della funzione incognita. - La relazione fra integrale indefinito e integrale definito è il
Teorema fondamentale del calcolo integrale:
![\int_a^bf(x)dx=\left[\int f(x)dx)\right]_a^b](../../../_images/math/7ac55c0058f3bef498832850f4333ca1b46559e4.png) . La formula indica il
procedimento per calcolare un integrale definito: basta calcolare la differenza
fra le due primitive agli estremi di integrazione.
. La formula indica il
procedimento per calcolare un integrale definito: basta calcolare la differenza
fra le due primitive agli estremi di integrazione. - Una tecnica di calcolo della primitiva assai utile è la sostituzione della
variabile. Si tratta in pratica di riscrivere la funzione integranda, operando
una opportuna trasformazione della variabile
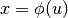 . La conseguenza
è che l’integrale viene trasformato:
. La conseguenza
è che l’integrale viene trasformato: 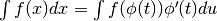 .
. - L’integrazione per parti è una tecnica utile nell’integrare il prodotto
di due funzioni. Segue questa formula:
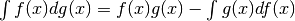 .
.
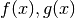 si chiamano parti finite.
si chiamano parti finite. 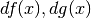 si dicono
parti infinitesime. Il punto di partenza è accorgersi che uno dei due fattori,
dei quali si vuole integrare il prodotto, è una parte infinitesima, cioè esprime
un differenziale e quindi si può riconoscere la sua primitiva. L’integrazione
per parti non garantisce di facilitare il calcolo. Le difficoltà sono legate,
in particolare, all’ultimo integrale della formula.
si dicono
parti infinitesime. Il punto di partenza è accorgersi che uno dei due fattori,
dei quali si vuole integrare il prodotto, è una parte infinitesima, cioè esprime
un differenziale e quindi si può riconoscere la sua primitiva. L’integrazione
per parti non garantisce di facilitare il calcolo. Le difficoltà sono legate,
in particolare, all’ultimo integrale della formula. - La costante
 che si esprime in
che si esprime in 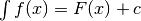 è implicita
nel segno di integrazione, cioè fa parte di tutti gli integrali indefiniti.
Esprime il fatto che la soluzione di un integrale indefinito non è una funzione
ma un insieme infinito di funzioni, diverse una dall’altra per il variare di
è implicita
nel segno di integrazione, cioè fa parte di tutti gli integrali indefiniti.
Esprime il fatto che la soluzione di un integrale indefinito non è una funzione
ma un insieme infinito di funzioni, diverse una dall’altra per il variare di  .
. - Mentre l’integrale definito è un numero, l’integrale indefinito è una famiglia infinita di primitive.
Esercizi¶
- Dimostra che la primitiva della differenza vale la differenza delle primitive.
- Dimostra che cercare il prodotto fra una costante e la primitiva di una funzione equivale a cercare la primitiva del prodotto fra la costante e la funzione. Svolgi la dimostrazione nei due sensi.
- Perchè non si può scrivere
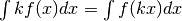 ?
? - Dimostra le tre formule che coinvolgono la cotangente.
- Calcola
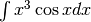
- Calcola
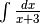 , facendo uso di una opportuna sostituzione.
, facendo uso di una opportuna sostituzione.
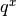
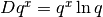 ricaviamo
ricaviamo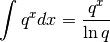
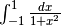 e visualizza il suo significato geometrico.
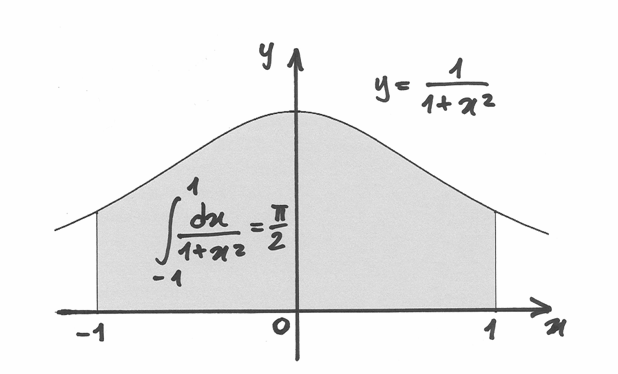
e visualizza il suo significato geometrico.![\int_{-1}^1\frac{dx}{1+x^2}=\left[\arctan x +c\right]_{-1}^1=\arctan 1-\arctan(-1)=
\frac{\pi}{4}- \frac{-\pi}{4}= \frac{\pi}{2}](../../../_images/math/5736bb7567bad9809deeefb1f3fada978c529574.png)
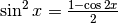 .
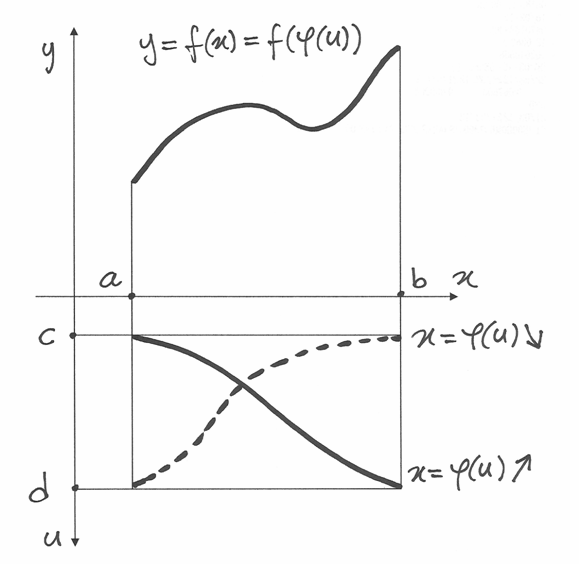
.![\int \sin^2 xdx=\int \frac{1-\cos 2x}{2}dx=&\frac{1}{2}\int(1-\cos 2x)dx=
\frac{1}{2}\int dx-\frac{1}{2}\int \cos 2x dx=\frac{x}{2}-\frac{1}{2}\frac{\sin 2x}{2}+c\\
&\mbox{quindi: }\\
\int_0^\frac{\pi}{2} \sin^2 xdx=&\left[\frac{x}{2}-
\frac{\sin 2x}{4} \right]_0^\frac{\pi}{2}=\frac{\pi}{4}.](../../../_images/math/c4b7163647815e5f78ad17be3830cb12361ccbf7.png)
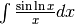
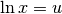 , da cui deriva che
, da cui deriva che 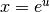 e
e 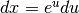 .
.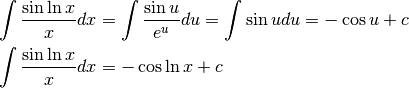
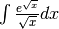
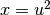 e
e