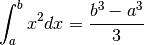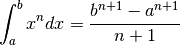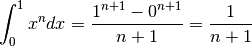L’integrale definito¶
Le primitive di una funzione a dominio continuo¶
Supponiamo di conscere i valori di una funzione  , definita su un
intervallo
, definita su un
intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , che sappiamo essere la derivata di una funzione
incognita
, che sappiamo essere la derivata di una funzione
incognita 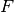 , dfinita sempre su
, dfinita sempre su ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) . Il problema che ci
poniamo è se sia possibile risalire ai valori di
. Il problema che ci
poniamo è se sia possibile risalire ai valori di 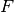 , a partire dai
vlori della sua derivata
, a partire dai
vlori della sua derivata  . Da un punto di vista geometrico si tratta
di ricostruire il grafico (o uno dei grafici) di una funzione, conoscendone
la pendenza in corrispondenza di ogni valore di
. Da un punto di vista geometrico si tratta
di ricostruire il grafico (o uno dei grafici) di una funzione, conoscendone
la pendenza in corrispondenza di ogni valore di  . L’analogo cinematico
è ricostruire la posizione di un corpo mobile, conoscendone la velocità.
. L’analogo cinematico
è ricostruire la posizione di un corpo mobile, conoscendone la velocità.
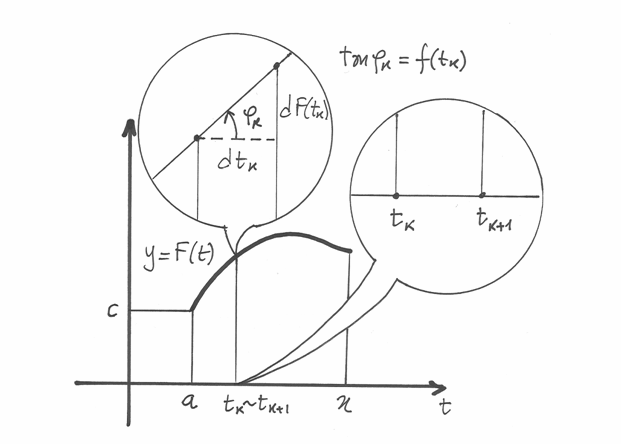
Si tratta di un problema con infinite soluzioni perché la posizione ad ogni istante dipende anche dalla posizione che il mobile aveva inizialmente. Questo, nel caso geometrico, significa che otterremo grafici paralleli diversi in corrispondenza di diversi valori iniziali in ordinata.
Supponiamo che sia 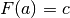 . Conoscendo
. Conoscendo  (a meno di infinitesimi
di ordine superiore a
(a meno di infinitesimi
di ordine superiore a 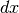 ) possiamo ricavare
) possiamo ricavare 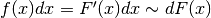 ,
cioè possiamo ricavare il valore di
,
cioè possiamo ricavare il valore di 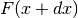 conoscendo quello di
conoscendo quello di 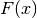 .
Per ricostruire il valore di
.
Per ricostruire il valore di 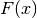 a partire da
a partire da 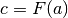 , dividiamo
l’intervallo
, dividiamo
l’intervallo ![[a,x]](../../../_images/math/fc48bc5c76e6c928e4c1c9a33f641fc6b2a4091b.png) in infiniti intervallini infinitesimi, individuati
dai punti
in infiniti intervallini infinitesimi, individuati
dai punti 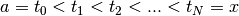 con
con 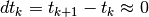 .
Ne consegue
.
Ne consegue
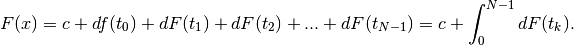
Ma, dato che 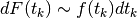 , si ha
, si ha
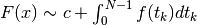 .
.
Seguendo l’analogia cinematica, è come dire che la posizione all’istante
 di un punto su una retta si ottiene in base allo spostamento effettuato
a partire dalla posizione iniziale. Lo spostamento, poi, è calcolabile con
l’integrale degli spostamenti infinitesimi
di un punto su una retta si ottiene in base allo spostamento effettuato
a partire dalla posizione iniziale. Lo spostamento, poi, è calcolabile con
l’integrale degli spostamenti infinitesimi 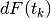 effettuati in
corrispondenza degli intervalli infinitesimi di tempo
effettuati in
corrispondenza degli intervalli infinitesimi di tempo 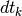 . Gli
spostamenti infinitesimi sono stati approssimati, in modo indistinguibile,
dai prodotti delle velocità iniziali
. Gli
spostamenti infinitesimi sono stati approssimati, in modo indistinguibile,
dai prodotti delle velocità iniziali 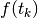 per le corrispondenti durate
infinitesime
per le corrispondenti durate
infinitesime 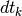 .
.
L’interpretazione geometrica è: 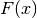 è un numero, che fornisce
l’ordinata di una funzione definita su un intervallo
è un numero, che fornisce
l’ordinata di una funzione definita su un intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , della quale conosciamo
l’ordinata iniziale
, della quale conosciamo
l’ordinata iniziale  e la pendenza
e la pendenza  in ogni punto.
in ogni punto.
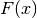 si ottiene sommando a
si ottiene sommando a  gli infiniti
incrementi infinitesimi
gli infiniti
incrementi infinitesimi 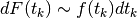 che
che 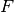 realizza
negli infiniti intervalli infinitesimi che suddividono
realizza
negli infiniti intervalli infinitesimi che suddividono ![[a,x]](../../../_images/math/fc48bc5c76e6c928e4c1c9a33f641fc6b2a4091b.png) .
.
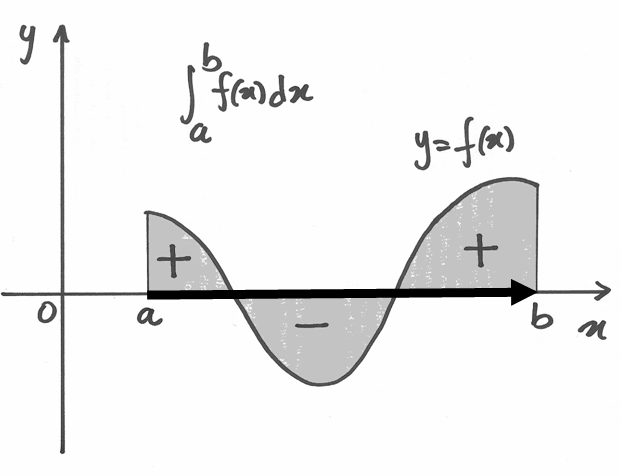
L’integrale e l’area¶
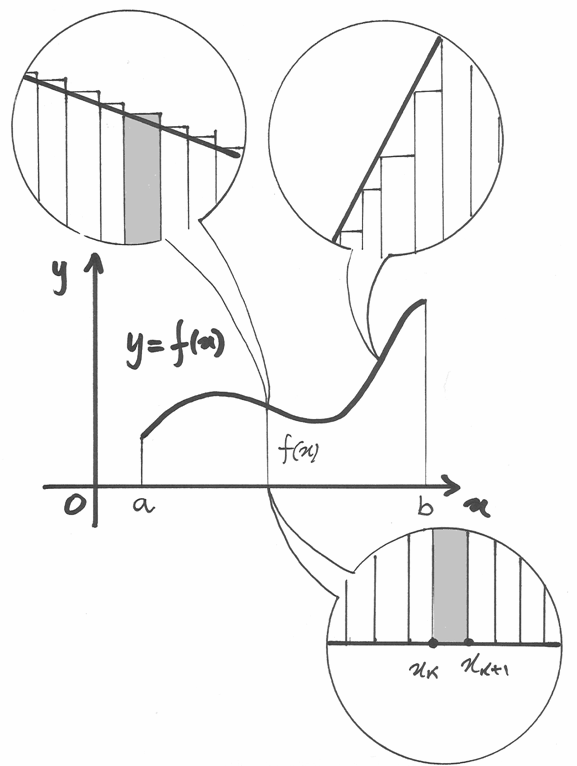
Siamo arrivati al punto che i valori di una primitiva si ottengono tramite il calcolo di
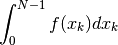
dove  è definita su un certo intervallo
è definita su un certo intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , che viene suddiviso
in infinite porzioni infinitesime
, che viene suddiviso
in infinite porzioni infinitesime 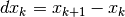 segnate dai punti
segnate dai punti
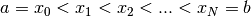 .
.
Quale è il significato geometrico di tale integrale ed è un signifato valido generalmente oppure dipende dalla suddivisione che abbiamo operato nell’intervallo?
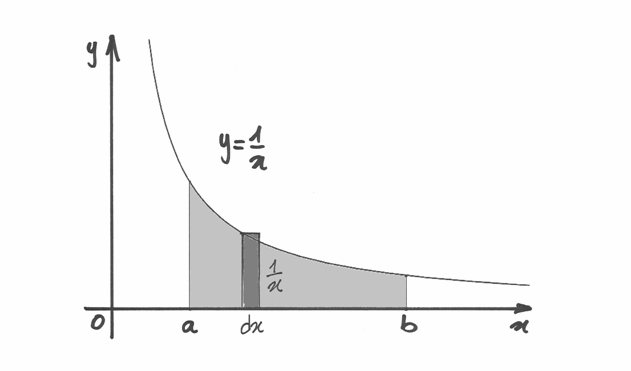
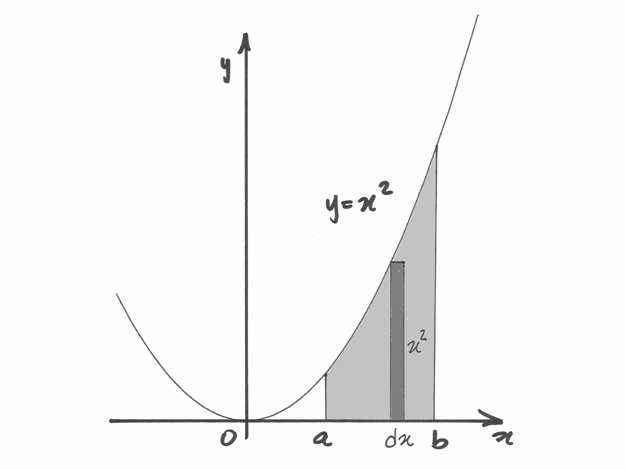
Consideriamo il grafico della funzione 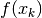 . Il prodotto
. Il prodotto 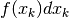 corrisponde all’area del rettangolo di base infinitesima
corrisponde all’area del rettangolo di base infinitesima 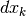 (corrisponde all’ampiezza dell’intervallo
(corrisponde all’ampiezza dell’intervallo ![[x_k,x_{k+1}]](../../../_images/math/5446057f54ec360dabac9be7e526d7787a2a6a0f.png) ) e altezza
pari all’ordinata
) e altezza
pari all’ordinata 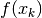 (cioè il segmento verticale da
(cioè il segmento verticale da 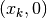 a
a 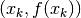 . Tale ordinata può anche essere negativa e quindi
il rettangolo può svilupparsi, infinitamente sottile, sopra o sotto l’asse
. Tale ordinata può anche essere negativa e quindi
il rettangolo può svilupparsi, infinitamente sottile, sopra o sotto l’asse  .
Se la funzione è continua, allora l’integrale
.
Se la funzione è continua, allora l’integrale
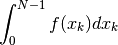
è indistinguibile dall’area della regione di piano compresa tra il grafico della
funzione, l’asse delle ascisse e le rette vericali 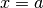 e
e 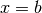 .
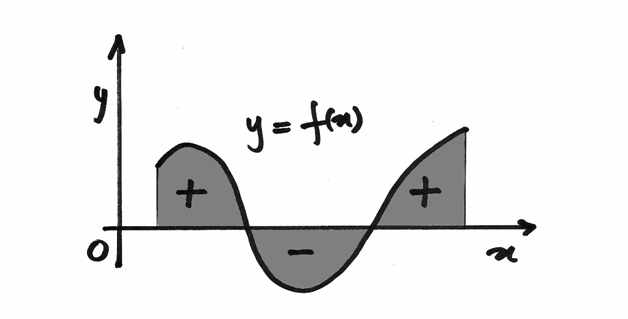
L’area è presa con il segno positivo nel semipiano superiore e negativo
nel semipiano inferiore.
.
L’area è presa con il segno positivo nel semipiano superiore e negativo
nel semipiano inferiore.
La parte standard dell’integrale non dipende dalla particolare scelta dei
punti di suddivisione 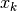 , nè dal loro numero ipernaturale infinito
, nè dal loro numero ipernaturale infinito
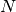 , ma solo dalla funzione e dagli estremi dell’intervallo.
, ma solo dalla funzione e dagli estremi dell’intervallo.
Possiamo quindi tralasciare i dettagli, scrivere
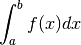
e chiamarlo integrale definito della funzione  nell’intervallo
nell’intervallo
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) .
.
Primi esempi¶
La funzione è una retta¶
Il primo esempio è volutamente molto semplice e ha soluzione immediata. Ma ci serve per verificare tutti i punti della trattazione precedente. Calcoliamo
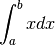
Il risultato sarà il numero che si ottiene dividendo l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) in infinite parti infinitesime, mediante i punti
in infinite parti infinitesime, mediante i punti 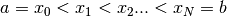 ,
e prendendo la parte standard dell’integrale
,
e prendendo la parte standard dell’integrale 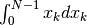 .
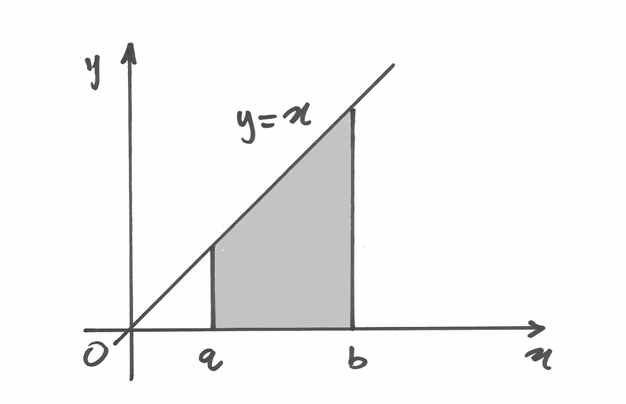
Possiamo anticipare il risultato del calcolo osservando la figura: si tratta
di un trapezio di basi
.
Possiamo anticipare il risultato del calcolo osservando la figura: si tratta
di un trapezio di basi  e
e 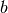 e altezza
e altezza 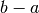 , quindi
di area
, quindi
di area 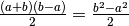 . Ma applichiamo il
procedimento esattamente come lo abbiamo descritto, in due modi diversi.
. Ma applichiamo il
procedimento esattamente come lo abbiamo descritto, in due modi diversi.
Suddivisione in progressione aritmetica¶
Dividiamo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) nel modo più semplice, cioè in infiniti intervalli di uguale
ampiezza
nel modo più semplice, cioè in infiniti intervalli di uguale
ampiezza 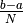 . I punti di suddivisione sono
. I punti di suddivisione sono
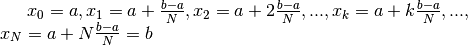 .
L’ampiezza è costante
.
L’ampiezza è costante 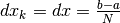 per
per 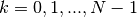 .
Applichiamo la definizione di integrale:
.
Applichiamo la definizione di integrale:
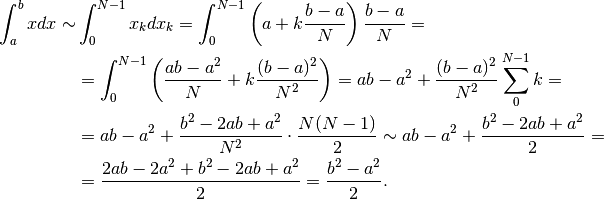
Suddivisione in progressione geometrica¶
Ora ricalcoliamo l’integrale con una suddivisione diversa, segnata dai punti
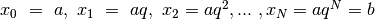 . Ricaviamo da quest’ultima che
. Ricaviamo da quest’ultima che
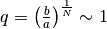 , per cui
, per cui 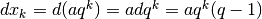 quindi
quindi
![\int_a^b x dx\sim &\int_0^{N-1}x_kdx_k=\int_0^{N-1}aq^k\cdot aq^k(q-1)=a^2(q-1)\sum_0^{N-1}q^{2k}=\\
&=a^2(q-1)\sum_0^{N-1}(q^2)^k=a^2(q-1)\left[\frac{q^{2k}}{q^2-1}\right]_0^N=a^2(q-1)\frac{q^{2N}-1}{q^2-1}=\\
&=a^2(q-1)\frac{\left(\frac{b}{a}\right)^2-1}{(q-1)(q+1)}=a^2\frac{\frac{b^2-a^2}{a^2}}{q+1}
=\frac{b^2-a^2}{q+1}\sim\frac{b^2-a^2}{2}.](../../../_images/math/b73d17b0aea252608fc3b80679bf22947d16d37a.png)
Con questo doppio calcolo abbiamo dimostrato che il risultato non dipende dal tipo di suddivisione adottata. Inoltre si vede bene che anche l’esercizio più semplice non è di svolgimento immediato.
Integrale definito di 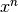 ¶
¶
Sappiamo che (usiamo per brevità il segno di uguaglianza)
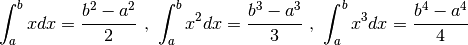
(quest’ultimo risultato è dato negli esercizi). Per cui potremmo aspettarci:
Infatti:
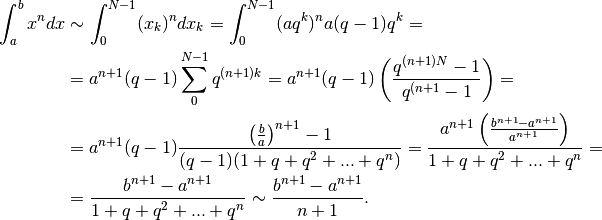
Se l’esponente è nullo o negativo¶
La formula dell’integrale definito di funzioni potenza si applica anche in caso
di esponente nullo o negativo. Infatti, per 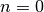 si ha (ed è un’uguaglianza
esatta perchè si ottiene la lunghezza dell’intervallo):
si ha (ed è un’uguaglianza
esatta perchè si ottiene la lunghezza dell’intervallo):
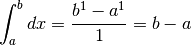
Ricaviamo il risultato per i casi 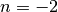 e
e 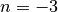 applicando la definizione di integrale,
mentre lasciamo per esercizio la verifica dei risultati con l’uso della formula generale delle
funzioni potenza. Notiamo, in premessa, che se l’esponente è negativo l’intervallo
applicando la definizione di integrale,
mentre lasciamo per esercizio la verifica dei risultati con l’uso della formula generale delle
funzioni potenza. Notiamo, in premessa, che se l’esponente è negativo l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) non può includere l’origine.
non può includere l’origine.
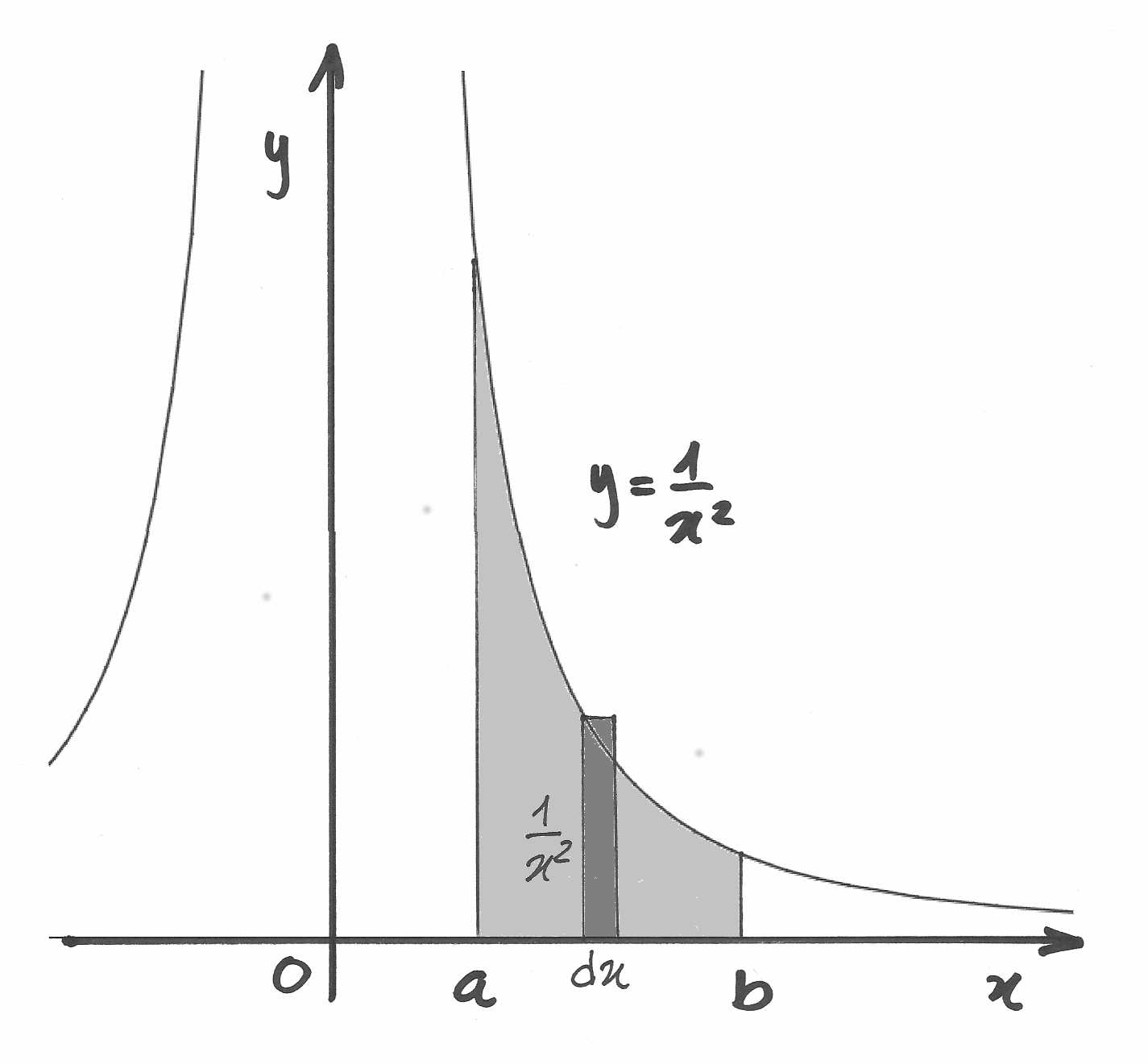
Se 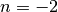 si ha:
si ha:
![\int_a^bx^{-2}dx&=\int_a^b\frac{dx}{x^2}\sim \int_0^{N-1}\frac{dx_k}{x_k^2}=
\int_0^{N-1}\frac{a(q-1)q^k}{(aq^k)^2}=\int_0^{N-1}\frac{(q-1)}{aq^k}=
\frac{q-1}{a}\sum_0^{N-1}\left(\frac{1}{q}\right)^k=\\
&=\frac{q-1}{a}\left[\frac{\left(\frac{1}{q}\right)^k}{1-\frac{1}{q}}\right]_0^N=
\frac{q-1}{a}\cdot\frac{\left(\frac{1}{q}\right)^N -1}{1-\frac{1}{q}}=
\frac{q-1}{a}\cdot \frac{\frac{a}{b}-1}{\frac{q-1}{q}}=q\left(\frac{1}{b}-\frac{1}{a}\right)
\sim\frac{1}{b}-\frac{1}{a}.](../../../_images/math/a768765f599c5960e7f2c46f13ee8194fbb00fe5.png)
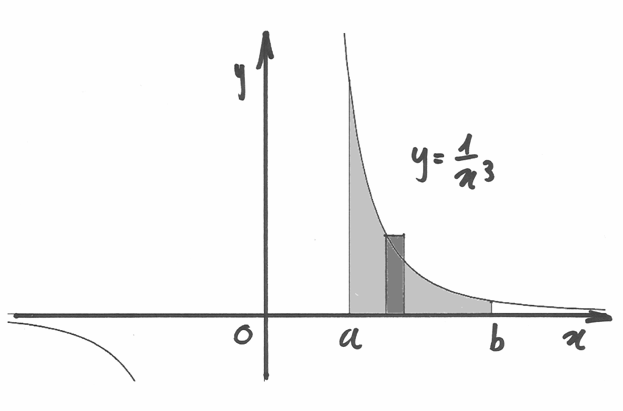
Se 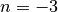 si ha:
si ha:
![\int_a^bx^{-3}dx&=\int_a^b\frac{dx}{x^3}\sim \int_0^{N-1}\frac{dx_k}{x_k^3}=
\int_0^{N-1}\frac{a(q-1)q^k}{(aq^k)^3}=
\frac{q-1}{a^2}\sum_0^{N-1}\frac{1}{q^{2k}}=\\
&=\frac{q-1}{a^2}\left[\frac{q^{\frac{1}{2N}-1}}{\frac{1}{q^2}-1}\right]=
\frac{q-1}{a^2}\frac{\left(\frac{a}{b}\right)^2-1}{\frac{1-q^2}{q^2}}=
\frac{q-1}{a^2}\frac{\frac{a^2-b^2}{b^2}}{\frac{(1-q)(1+q)}{q^2}}=\\
&=\frac{b^2-a^2}{a^2b^2}\frac{q^2}{1+q}\sim\frac{b^2-a^2}{2a^2b^2}=
\frac{1}{2}\left(\frac{1}{a^2}-\frac{1}{b^2}\right).](../../../_images/math/c2f836f304685998391417c8a946eecae2a9b60f.png)
Integrale definito di 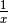 ¶
¶
Se l’esponente della funzione potenza è 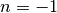 abbiamo un problema:
basta applicare la regola generale per rendersene conto. Cerchiamo quindi
l’integrale definito attraverso la definizione.
abbiamo un problema:
basta applicare la regola generale per rendersene conto. Cerchiamo quindi
l’integrale definito attraverso la definizione.
![\int_0^b\frac{dx}{x}\sim\int_0^{N-1}\frac{dx_k}{x_k}=\int_0^{N-1}\frac{a(q-1)q^k}{aq^k}=
\sum_0^{N-1}(q-1)=N(q-1)=N\left[\left(\frac{b}{a}\right)^{\frac{1}{n}}-1\right].](../../../_images/math/7bff234931ed8df38be2726e9cc267000d1a2551.png)
Il risultato è una forma indeterminata, che deve essere risolvibile perchè
anche il disegno ci mostra l’esistenza della parte standard del risultato.
Poniamo che questo sia  . Abbiamo allora
. Abbiamo allora
![N\left[\left(\frac{b}{a}\right)^{\frac{1}{n}}-1\right]\sim s\ \to\
\left(\frac{b}{a}\right)^{\frac{1}{n}}-1\sim\frac{s}{N}\ \to\
&\left(\frac{b}{a}\right)^{\frac{1}{n}}\sim 1+\frac{s}{N}\ \to\
\frac{b}{a}\sim \left(1+\frac{s}{N}\right)^N\ \sim e^s\\
\frac{b}{a}= e^s\ \to\ &s=\ln\frac{b}{a}\\
\int_a^b\frac{dx}{x}=&\ln\frac{b}{a}](../../../_images/math/ae2ff5b5dc96c8e7f420f6d635d33092e2851d3c.png)
Aree sottese alle curve 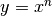 ¶
¶
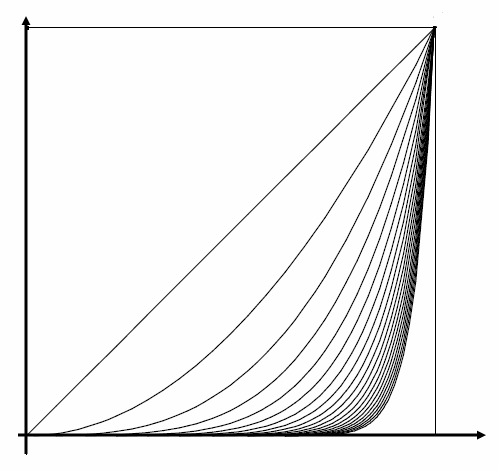
Le funzioni 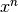 , con
, con 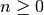 hanno grafici progressivamente più
adagiati sull’asse
hanno grafici progressivamente più
adagiati sull’asse  , nell’intervallo
, nell’intervallo ![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) , man mano che cresce
l’esponente. Se consideriamo le aree sottese alle diverse curve in quest’intervallo
possiamo notare come esse siano sempre più piccole al crescere dell’esponente.
Per
, man mano che cresce
l’esponente. Se consideriamo le aree sottese alle diverse curve in quest’intervallo
possiamo notare come esse siano sempre più piccole al crescere dell’esponente.
Per 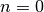 l’area è quella di un quadrato di lato
l’area è quella di un quadrato di lato 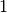 , quindi l’area vale
, quindi l’area vale 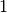 .
Per
.
Per 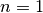 l’area è quella di metà quadrato, vale quindi
l’area è quella di metà quadrato, vale quindi  .
Nel caso generale l’area vale
.
Nel caso generale l’area vale
Area sottesa all’iperbole equilatera¶
Nel caso della funzione 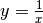 , l’area compresa fra il grafico,
l’asse orizzontale e la retta
, l’area compresa fra il grafico,
l’asse orizzontale e la retta 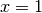 e
e 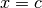 , con
, con  , è
, è
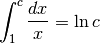
Il fatto che il logaritmo naturale sia così legato all’iperbole equilatera è da considerare importante e sarà approfondito più avanti.
Integrale definito di 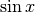 ¶
¶
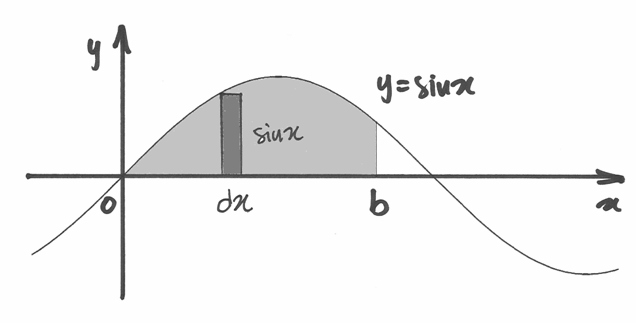
Per questo calcolo suddividiamo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) con punti in progressione aritmetica
e inizalmente scegliamo
con punti in progressione aritmetica
e inizalmente scegliamo 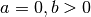 . Gli
. Gli 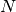 intervalli infinitesimi sono
contrasseganti dai punti
intervalli infinitesimi sono
contrasseganti dai punti 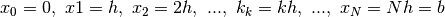 ,
con
,
con 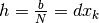 . Possiamo scrivere:
. Possiamo scrivere:
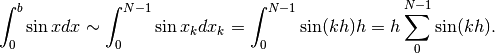
Il calcolo dell’ultima somma, che chiamiamo
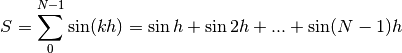
si esegue moltiplicato per  e poi ricorrendo alla formula
di Werner
e poi ricorrendo alla formula
di Werner 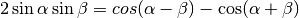
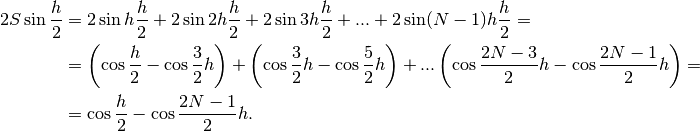
In sintesi:
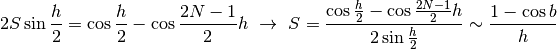
perché
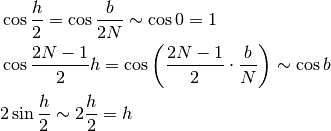
Concludiamo che
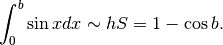
Il caso in cui 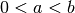 si deduce dal caso precedente pensando al significato
geometrico dell’integrale definito:
si deduce dal caso precedente pensando al significato
geometrico dell’integrale definito:
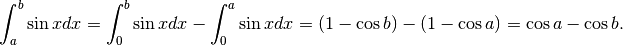
Se poi  , il risultato non cambia perché il seno è una funzione
periodica. Infatti basta prendere un intero
, il risultato non cambia perché il seno è una funzione
periodica. Infatti basta prendere un intero  abbastanza grande
per cui
abbastanza grande
per cui 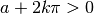 e il risultato sarà:
e il risultato sarà:
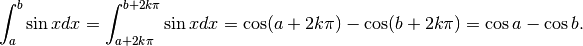
Proprietà dell’integrale definito¶
Dalle proprietà delle somme deriviamo direttamente le proprietà dell’integrale definito:
![&\int_a^bcdx=c(b-a)\\
&\int_a^b[cf(x)]dx=c\int_a^bf(x)dx\\
&\int_a^b[f(x)\pm g(x)]dx=\int_a^bf(x)dx\pm\int_a^bg(x)dx\\
&\mbox{se }f(x)\le g(x)\mbox{ allora }\int_a^bf(x)dx\le\int_a^bg(x)dx\\
&\left|\int_a^bf(x)dx\right|\le\int_a^b|f(x)|dx](../../../_images/math/2a41e0b5962fc9a116167f2d0cb26c43e96f40ab.png)
Un esempio¶
Con queste proprietà possiamo calcolare, per esempio l’integrale definito di
funzioni polinomiali, come nel caso semplice seguente: ![\int_1^2[6x^2-8x+3]dx](../../../_images/math/3fa3d44ae09e57078e0f2d2645ac74fcd615da4d.png) .
.
![&\int_1^2[6x^2-8x+3]dx= \int_1^2 6x^2dx-\int_1^2 8xdx+\int_1^2 3dx=
6\int_1^2 x^2dx-8\int_1^2 xdx+3(2-1)=\\
&=6\frac{2^3-1^3}{3}-8\frac{2^2-1^2}{2}+3=14-12+3=5](../../../_images/math/8d60a54d3b3966d3e3119fd3d60015922841d619.png)
Sull’integrale definito vi sono due altri dettagli importanti da approfondire
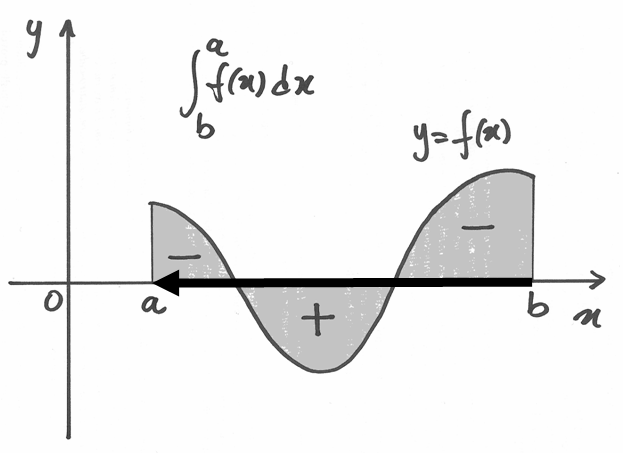
Il segno dell’integrale¶
Le somme, e quindi l’integrale, e quindi le primitive, hanno senso per  .
Se
.
Se  dovremmo integrare per così dire ‘a ritroso’, cioè da destra verso
sinistra, togliendo strisce di area infinitesima a partire dal valore F(a) che
in questo caso rappresenterebbe il risultato finale.
Infatti:
dovremmo integrare per così dire ‘a ritroso’, cioè da destra verso
sinistra, togliendo strisce di area infinitesima a partire dal valore F(a) che
in questo caso rappresenterebbe il risultato finale.
Infatti:
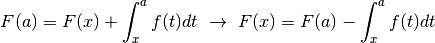
Infatti, l’integrazione a partire dall’estremo superiore significa utilizzare
intervalli infinitesimi di ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) per i quali il secondo estremo è a
sinistra del primo, quindi le differenze
per i quali il secondo estremo è a
sinistra del primo, quindi le differenze 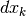 hanno segno negativo,
il che rende negative le aree dei rettangoli, come se fossero situati al
di sotto dell’asse
hanno segno negativo,
il che rende negative le aree dei rettangoli, come se fossero situati al
di sotto dell’asse  . Insomma, le aree di cui stiamo trattando non
sono le aree sempre positive delle figure geometriche tradizionali. Sono
aree orientate, il cui segno dipende sia dal segno di f in quegli intervalli,
sia dal verso di percorrenza dell’asse orizzontale.
. Insomma, le aree di cui stiamo trattando non
sono le aree sempre positive delle figure geometriche tradizionali. Sono
aree orientate, il cui segno dipende sia dal segno di f in quegli intervalli,
sia dal verso di percorrenza dell’asse orizzontale.
In conclusione è più semplice non cambiare la regola. Quindi la conserviamo, con queste precisazioni:
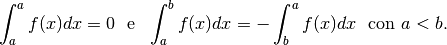
La somma di integrali¶
Una volta chiarita la situazione in cui l’integrale è nullo, possiamo utilizzarla come elemento neutro della somma e quindi trarre la relazione
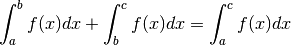
con 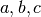 qualsiasi. La regola vale in ogni caso: per
qualsiasi. La regola vale in ogni caso: per 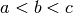 e
per
e
per 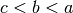 abbiamo già detto. Immaginiamo un terzo caso:
abbiamo già detto. Immaginiamo un terzo caso: 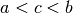 .
Allora
.
Allora
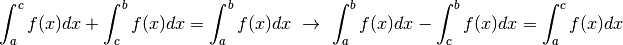
perché 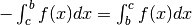 .
.
Risalire alla primitiva¶
Dopo i primi calcoli, torniamo a concentrarci sul problema della ricerca
della primitiva.
Sappiamo che se  è continua ed è la derivata di
è continua ed è la derivata di 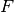 in
in ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) ,
allora
,
allora
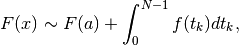
con 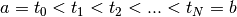 e
e 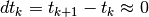 . Fissato
tutto questo, possiamo scrivere
. Fissato
tutto questo, possiamo scrivere
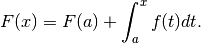
La continuità di  e la derivabilità di
e la derivabilità di 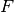 ci consentono di
esprimere tutto questo. Il fatto importante è che una funzione continua può
sempre essere pensata come derivata di un’altra funzione. Come nel caso discreto
chiameremo primitiva della funzione continua
ci consentono di
esprimere tutto questo. Il fatto importante è che una funzione continua può
sempre essere pensata come derivata di un’altra funzione. Come nel caso discreto
chiameremo primitiva della funzione continua  , definita in un intervallo,
ogni funzione
, definita in un intervallo,
ogni funzione 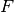 definita sullo stesso intervallo e avente f come tasso
di variazione, cioè come derivata. Esprimiamo tutto questo in termini più
matematici:
definita sullo stesso intervallo e avente f come tasso
di variazione, cioè come derivata. Esprimiamo tutto questo in termini più
matematici:
sia I un intervallo di numeri reali e sia 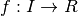 una funzione continua,
allora una qualsiasi funzione
una funzione continua,
allora una qualsiasi funzione 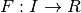 è una primitiva per f se
è una primitiva per f se
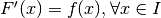 .
.
Abbiamo già ricavato l’espressione di F: 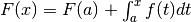 . Ora
dobbiamo dimostrare questa espressione ci garantisce che
. Ora
dobbiamo dimostrare questa espressione ci garantisce che 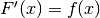 .
.
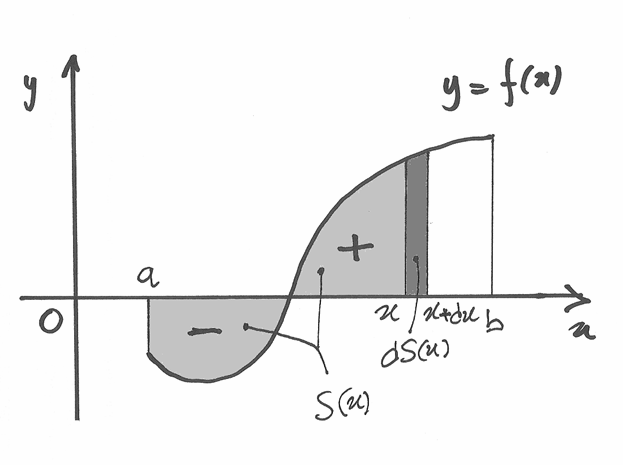
Chiamiamo 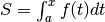 l’integrale che associa al numero
l’integrale che associa al numero 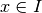 l’area della regione compresa fra il grafico di f, l’asse delle ascisse e le
rette verticali
l’area della regione compresa fra il grafico di f, l’asse delle ascisse e le
rette verticali 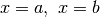 (l’area è negativa nel semipiano inferiore).
Allora
(l’area è negativa nel semipiano inferiore).
Allora 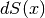 è l’area orientata della striscia di base dx, indistinguibile
dal rettangolo di area f(x)dx:
è l’area orientata della striscia di base dx, indistinguibile
dal rettangolo di area f(x)dx:
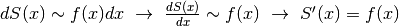 .
Poiché abbiamo definito
.
Poiché abbiamo definito 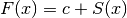 , è facile constatare che F’(x)=S’(x)=f(x).
, è facile constatare che F’(x)=S’(x)=f(x).
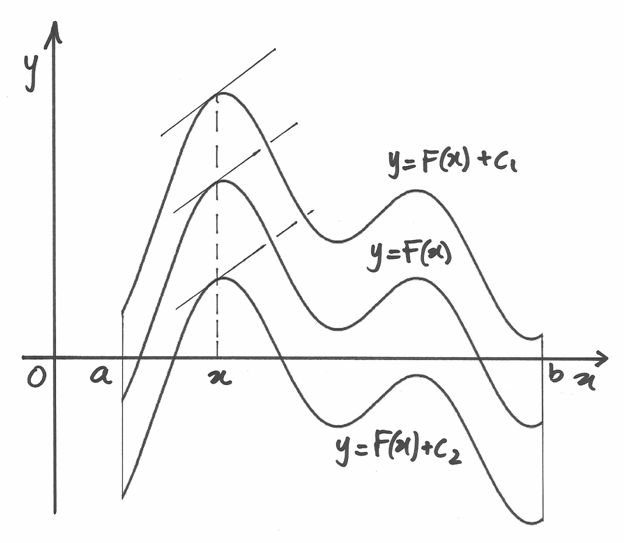
Quindi ogni funzione continua, definita su un intervallo, si può pensare come
derivata di infinite altre funzioni che differiscono fra loro solo per la scelta
della costante c. Questa rappresenta il valore della primitiva in a. 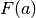 è un valore iniziale, sul quale si accumula la somma infinita.
Cambiare
è un valore iniziale, sul quale si accumula la somma infinita.
Cambiare 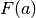 non influisce sul risultato della somma infinita,
ma solo sul risultato finale.
non influisce sul risultato della somma infinita,
ma solo sul risultato finale.
Quindi le primitive della stessa funzione sono infinite e i loro valori differiscono
per una costante. I loro grafici sono curve che si sviluppano parallelamente
nel piano cartesiano, a distanze diverse dall’asse  .
.
Un esempio¶
Cerchiamo tutte le primitive di 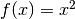 su R. Applichiamo la formula
con
su R. Applichiamo la formula
con 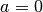
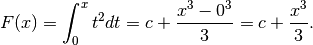
È facile verificare che ![D\left[c+\frac{x^3}{3}\right]=\frac{1}{3}(3x^2)=x^2](../../../_images/math/8154b9d00091f6a26dcf8cfad08a63e21c0eea36.png) .
.
Proviamo ora con a diverso. per esempio se 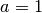
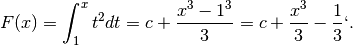
Al variare di 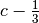 si trovano tutti i possibili valori che si
troverebbero variando il solo
si trovano tutti i possibili valori che si
troverebbero variando il solo  , quindi le due soluzioni si equivalgono.
La scelta di uno specifico valore
, quindi le due soluzioni si equivalgono.
La scelta di uno specifico valore  ha senso solo quando viene richiesta
una specifica primitiva. In questo caso si fa riferimento al fatto che
ha senso solo quando viene richiesta
una specifica primitiva. In questo caso si fa riferimento al fatto che 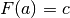 (vedi per esempio l’esercizio 8).
(vedi per esempio l’esercizio 8).
Il Teorema fondamentale¶
Finora abbiamo integrato solo poche funzioni semplici e ricavato
solo le regole di tre integrali notevoli: delle funzioni potenza, dell’iperbole
equilatera e della funzione seno. Grazie alle proprietà, possiamo svolgere esercizi
che prevedono varie combinazioni di queste funzioni, ma non possediamo un criterio
generale per integrare qualsiasi funzione. Anzi è giustificato il timore che
l’integrazione di una funzione diversa, per esempio una banale radice cubica,
comporti la complicata ricerca di una suddivisione opportuna di ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) e una difficile applicazione delle somme infinite. Come si è già
visto nel caso discreto, la conclusione è che non conviene calcolare gli integrali
per ottenere le primitive. Anzi, al contrario, conviene servirsi delle primitive
per calcolare gli integrali.
e una difficile applicazione delle somme infinite. Come si è già
visto nel caso discreto, la conclusione è che non conviene calcolare gli integrali
per ottenere le primitive. Anzi, al contrario, conviene servirsi delle primitive
per calcolare gli integrali.
Partiamo dalla formula 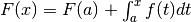 e poniamo
e poniamo 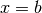 ,
usando x come variabile di integrazione. Allora
,
usando x come variabile di integrazione. Allora
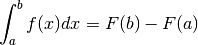
Si tratta del cosiddetto Teorema fondamentale del calcolo integrale, che indica che un integrale definito si può calcolare semplicemente con la differenza fra i valori della primitiva calcolati agli estremi di integrazione.
Il significato del Teorema fondamentale¶
Il significato geometrico del Teorema fondamentale è semplice: l’incremento
complessivo 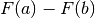 di una funzione
di una funzione 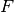 , primitiva di
, primitiva di  ,
nell’intervallo
,
nell’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , è l’integrale
, è l’integrale 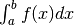 degli incrementi
infinitesimi che
degli incrementi
infinitesimi che  subisce negli infiniti intervallini infinitesimi in cui
subisce negli infiniti intervallini infinitesimi in cui
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) è stato suddiviso. Questi incrementi infinitesimi si ottengono, in
ogni intervallo, dal prodotto fra la pendenza iniziale di
è stato suddiviso. Questi incrementi infinitesimi si ottengono, in
ogni intervallo, dal prodotto fra la pendenza iniziale di  e la lunghezza
infinitesima dell’intervallino.
e la lunghezza
infinitesima dell’intervallino.
C’è un corrispondente significato cinematico, supponendo che 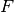 rappresenti
la legge oraria del moto e
rappresenti
la legge oraria del moto e  sia la velocità: lo spostamento complessivo
sia la velocità: lo spostamento complessivo
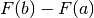 dall’istante
dall’istante  all’istante
all’istante 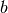 è l’integrale
è l’integrale
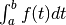 degli spostamenti infinitesimi che il punto mobile ha
compiuto negli infiniti intervalli infinitesimi in cui è stata suddivisa la durata.
degli spostamenti infinitesimi che il punto mobile ha
compiuto negli infiniti intervalli infinitesimi in cui è stata suddivisa la durata.
Dalle derivate alle primitive¶
Resta il problema di come ottenere le primitive senza integrare. C’e una strada spesso
non difficile, ricordando che ![D[F(x)]=f(x)](../../../_images/math/8451d9e6d225c8ea90e50534fb25034b613e787c.png) . Per esempio...
. Per esempio...
Esempi guida¶
1- Calcola 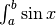 .
.
Ricordando che 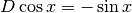 , si può immaginare che
, si può immaginare che 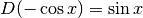 e quindi in questo caso
e quindi in questo caso 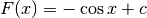 . Dal Teorema fondamentale abbiamo
subito la soluzione:
. Dal Teorema fondamentale abbiamo
subito la soluzione:
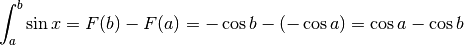
nello scrivere la soluzione abbiamo posto 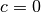 . Anche in caso di scelte diverse,
comunque,
. Anche in caso di scelte diverse,
comunque,  si sarebbe annullato nella differenza.
si sarebbe annullato nella differenza.
Il nuovo metodo è questo: occorre pensare a quale sia la funzione 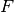 da
derivare per ottenere
da
derivare per ottenere  . Ricavata questa, si applica il Teorema fondamentale.
. Ricavata questa, si applica il Teorema fondamentale.
2- Calcola: 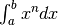 .
.
Ricordando la regola di derivazione ![D[x^n]=n x^{n-1}](../../../_images/math/fe4d3fc24129ae6e769731a200f787fb7a9112b1.png) , cerchiamo di ottenere
, cerchiamo di ottenere
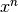 dalla derivata:
dalla derivata: ![D[x^{n+1}]=(n+1)x^n \ \to \ \frac{D[x^n]}{(n+1)}=x^n](../../../_images/math/e9847886149a82d6d53a3ee5980202862ca97f44.png) .
.
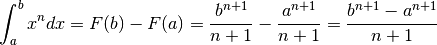
che non vale se 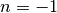 . Infatti...
. Infatti...
3- Calcola: 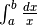 .
.
Poiché 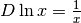 , una primitiva per
, una primitiva per  è
è 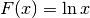 .
.
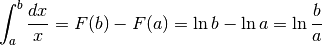
Riassunto¶
- Una funzione
 a dominio continuo in un intervallo
a dominio continuo in un intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) ha per primitive
ha per primitive 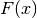 se
se 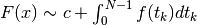 .
. - Trovare le primitive ha il significato di ricostruire i valori di una funzione conoscendo i valori delle sue derivate.
- Se
 è continua, l’integrale precedente ha il significato geometrico
dell’area sottesa al grafico di
è continua, l’integrale precedente ha il significato geometrico
dell’area sottesa al grafico di  nell’intervallo considerato. Negli
intervalli per i quali
nell’intervallo considerato. Negli
intervalli per i quali 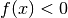 l’area assume segno negativo.
La parte standard dell’integrale non dipende dalla scelta operata su come
suddividere l’intervallo
l’area assume segno negativo.
La parte standard dell’integrale non dipende dalla scelta operata su come
suddividere l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) in parti infinitesime
in parti infinitesime 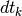 .
. - Con queste convenzioni, l’integrale si chiama integrale definito di
 fra
fra  e
e 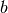 e si scrive
e si scrive 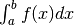 .
. - Applicando la definizione si dimostrano alcuni risultati importanti (le uguaglianze valgono per le parti standard):
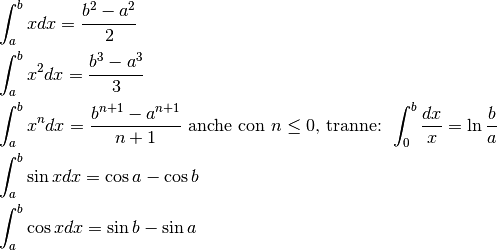
L’integrale definito relativo all’intervallo
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) ha senso con
ha senso con  .
Nei casi
.
Nei casi 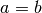 e
e 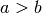 si ricavano le regole seguenti, che dipendono
dal verso di percorrenza dell’intervallo sull’asse
si ricavano le regole seguenti, che dipendono
dal verso di percorrenza dell’intervallo sull’asse 
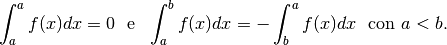
Vale inoltre la regola per la somma:
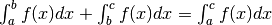 .
.Il Teorema fondamentale del calcolo integrale consente di calcolare gli integrali ricorrendo alle primitive:
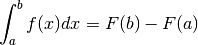
A questo punto è più conveniente calcolare le primitive senza far uso di integrali. Il metodo per ottenerle è di ragionare all’inverso rispetto all’operazione di derivazione.
Esercizi¶
- Dimostra, seguendo gli esempi nel dettaglio, che
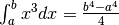 .
Per semplicità, usa la suddivisione in progressione geometrica.
.
Per semplicità, usa la suddivisione in progressione geometrica. - Applica la regola delle funzioni potenza nei seguenti casi:
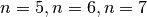
- Applica la regola delle funzioni potenza nei seguenti casi:
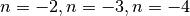
- Quanto vale l’area fra i grafici di due successive funzioni potenza
nell’intervallo
![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) ? Ricava il risultato tramite alcuni
esempi, poi formula la regola.
? Ricava il risultato tramite alcuni
esempi, poi formula la regola. - Calcola l’area sottesa all’iperbole equilatera nel caso di
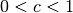 .
. - Dimostra che
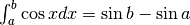 , seguendo punto per
punto il ragionamento usato per dimostrare la formula dell’integrale definito
della funzione seno.
, seguendo punto per
punto il ragionamento usato per dimostrare la formula dell’integrale definito
della funzione seno. - Esprimi la regola della somma di integrali definiti con
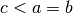 .
. - Cerca, fra le infinite primitive di
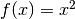 , quella che vale 2
per
, quella che vale 2
per 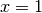 .
. - Calcola
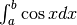 applicando il Teorema fondamentale.
applicando il Teorema fondamentale. - Se l’intervallo
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) è di numeri negativi, vale ancora l’ultimo
esempio del capitolo?
è di numeri negativi, vale ancora l’ultimo
esempio del capitolo?
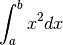
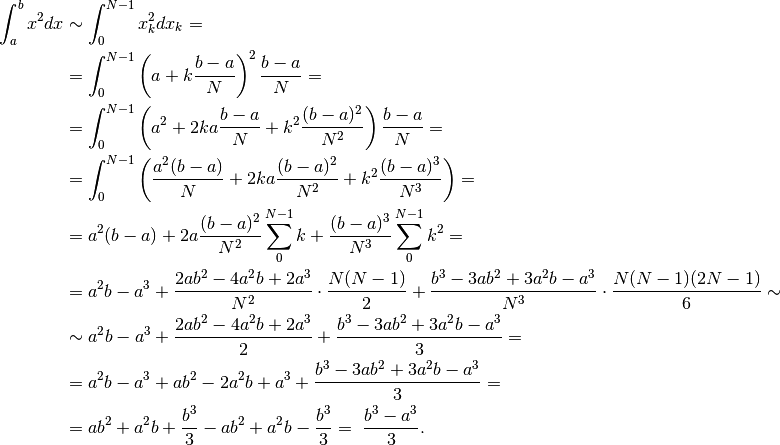
![\int_a^bx^2dx& \sim \int_0^{N-1}x^2_kdx_k = \int_0^{N-1}(aq^k)^2aq^k(q-1)=
a^3(q-1)\sum_0^{N-1}q^{3k}=\\
&=a^3(q-1)\left[\frac{q^3}{^3-1}\right]_0^{N-1}=a^3(q-1)\frac{q^{3N}-1}{q^3-1}=
a^3\frac{\frac{b^3}{a^3}-1}{q^2+q+1}=\frac{b^3-a^3}{q^2+q+1}.](../../../_images/math/20d2b25915480cb585a006ba259900d90cfb156c.png)
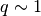 , concludiamo che:
, concludiamo che: