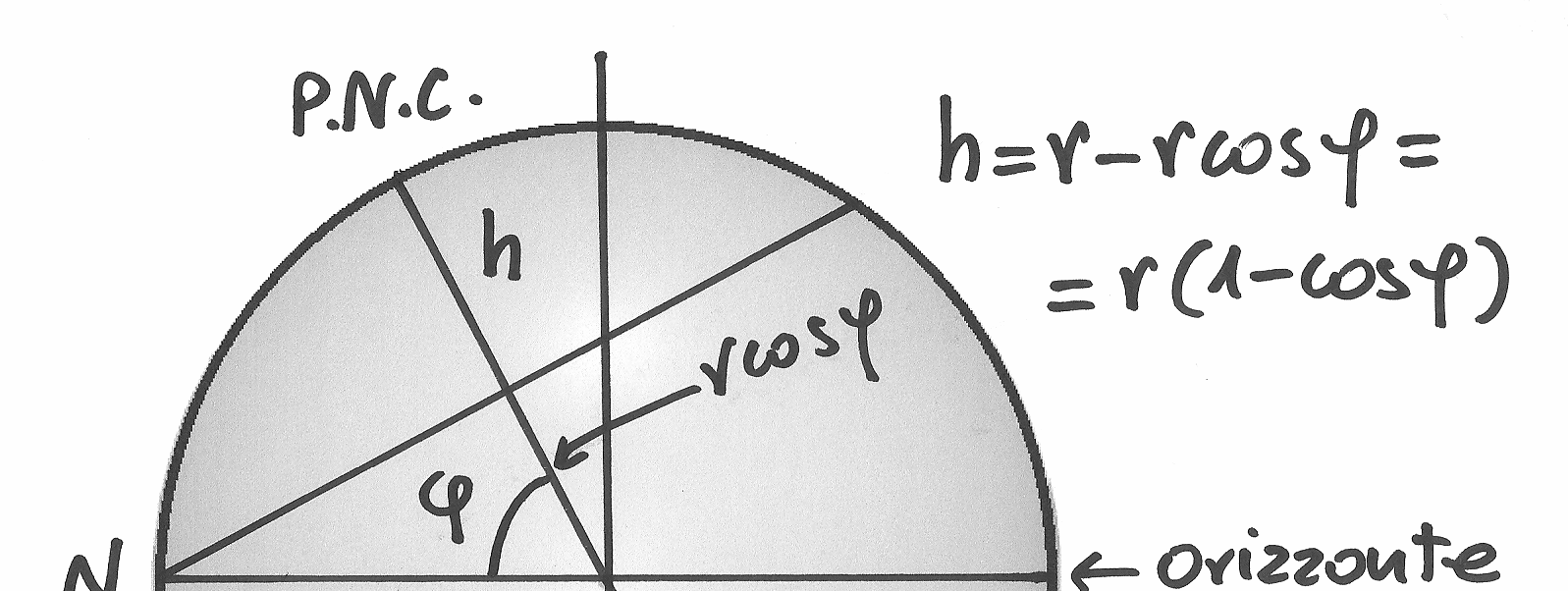Le primitive delle funzioni e l’integrale¶
Le primitive delle funzioni a dominio discreto¶
Come già visto nel libro del calcolo differenziale, chiamiamo funzione a
dominio discreto una funzione a valori reali 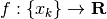 il cui dominio è una successione crescente di valori distinti
il cui dominio è una successione crescente di valori distinti  .
Si tratta quindi di una funzione il cui grafico è dato da una successione di
punti distinti
.
Si tratta quindi di una funzione il cui grafico è dato da una successione di
punti distinti  , con
, con 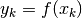 . Per queste funzioni
abbiamo definito il tasso di variazione come il rapporto incrementale relativo
all’indice
. Per queste funzioni
abbiamo definito il tasso di variazione come il rapporto incrementale relativo
all’indice  , cioè il numero
, cioè il numero 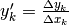 .
.
La primitiva della funzione 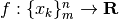 è la funzione
è la funzione
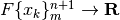 che ha la funzione
che ha la funzione  come tasso
di variazione. Se poniamo
come tasso
di variazione. Se poniamo 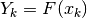 , allora la precedente definizione
di primitiva ha per conseguenza
, allora la precedente definizione
di primitiva ha per conseguenza 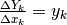 ,
e quindi
,
e quindi 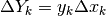 . Una generica primitiva sarà quindi
. Una generica primitiva sarà quindi
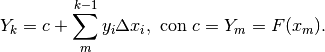
Tutto questo somiglia alla ricerca della primitiva di una
successione, ma nel caso attuale il valore 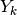 si riferisce al numero reale
si riferisce al numero reale 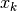 , non all’indice intero
, non all’indice intero  .
.
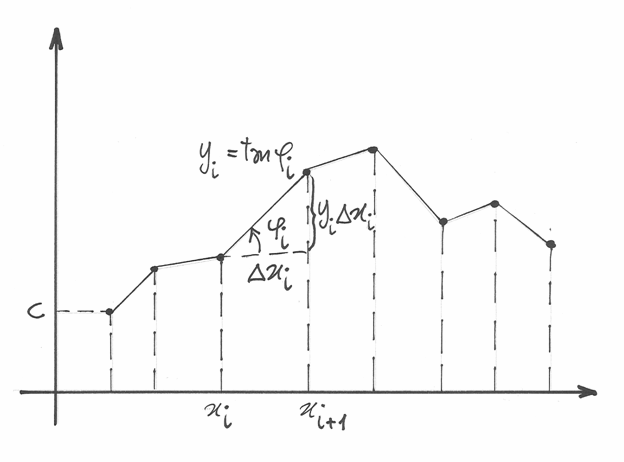
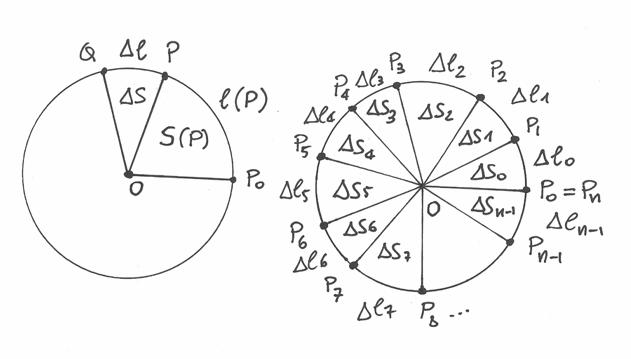
Dal punto di vista geometrico, ricercare i valori di una funzione a dominio
discreto a partire dai suoi tassi di variazione significa ricostruire una
spezzata a partire dalle pendenze dei suoi segmenti. Infatti nei vari
intervalli da 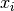 a
a 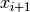 , gli incrementi della funzione
lungo l’asse delle ordinate sono dati dai vari
, gli incrementi della funzione
lungo l’asse delle ordinate sono dati dai vari 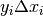 .
.
A partire da un arbitrario valore  , il k_esimo valore della
primitiva risulterà dalla somma di tutti gli incrementi precedenti, cioè
, il k_esimo valore della
primitiva risulterà dalla somma di tutti gli incrementi precedenti, cioè
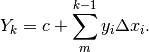
C’è un secondo modo, assai espressivo, di rappresentare geometricamente
questa somma se immaginiamo, per un momento, di trascurare la costante
 , per esempio ponendola uguale a zero.
, per esempio ponendola uguale a zero.
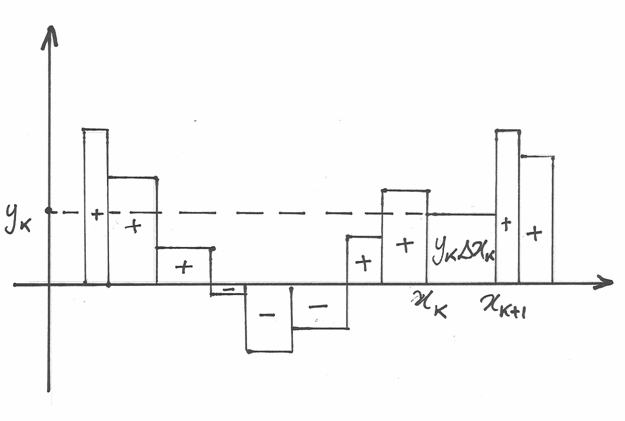
Un generico prodotto 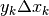 rappresenta l’area di un
rettangolino di base
rappresenta l’area di un
rettangolino di base 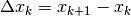 e altezza
e altezza 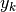 ,
sicché
,
sicché 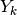 , secondo la formula precedente, rappresenta l’area
complessiva del plurirettangolo, nel quale alcune parti possono anche avere
area negativa, come illustra l’immagine.
, secondo la formula precedente, rappresenta l’area
complessiva del plurirettangolo, nel quale alcune parti possono anche avere
area negativa, come illustra l’immagine.
Definizione di integrale¶
A questo punto, i concetti appresi si potrebbero trasferire alle funzioni che hanno dominio continuo. Si tratterebbe di ricostruire i valori della primitiva (delle primitive) di una funzione, conoscendo i suoi tassi di variazione, cioè le derivate, relativi a intervalli infinitesimi, di riscrivere le somme precedenti nel modo opportuno e di visualizzare graficamente il significato di quanto risulta.
Questa volta, però, preferiamo partire da una definizione più generale, cioè utile sia per i problemi che stiamo affrontando, sia in altri casi.
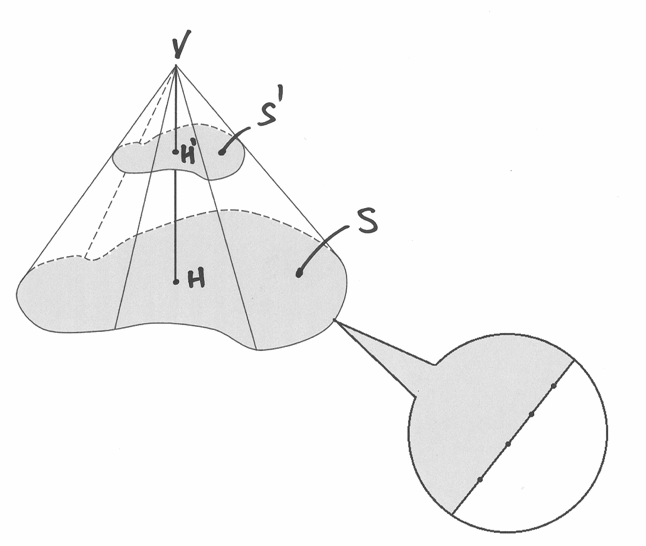
Definiamo integrale la somma di un numero ipernaturale infinito di numeri
infinitesimi, cioè una somma del tipo 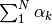 (gli
(gli
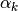 sono infinitesimi,
sono infinitesimi, 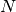 è un numero ipernaturale infinito).
È un concetto così importante che, come per la derivata, è identificato da un
particolare simbolo, questo:
è un numero ipernaturale infinito).
È un concetto così importante che, come per la derivata, è identificato da un
particolare simbolo, questo: 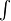 , cioè una esse stilizzata, usata
storicamente per esprimere questa particolare somma. Scriveremo quindi
, cioè una esse stilizzata, usata
storicamente per esprimere questa particolare somma. Scriveremo quindi
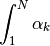
invece di 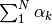 . Il risultato di una tale somma può essere di
qualsiasi tipo, come si capisce da questi esempi elementari:
. Il risultato di una tale somma può essere di
qualsiasi tipo, come si capisce da questi esempi elementari:
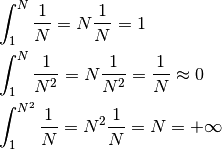
Non si tratta quindi di una forma sempre indeterminata, come dovrebbe essere per un semplice prodotto tra infiniti e infinitesimi.
Primi esempi di calcolo¶
La circonferenza¶
Sappiamo già che 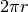 è la formula che fornisce la misura di una
circonferenza di raggio
è la formula che fornisce la misura di una
circonferenza di raggio  . Vediamo come ricavarla.
. Vediamo come ricavarla.
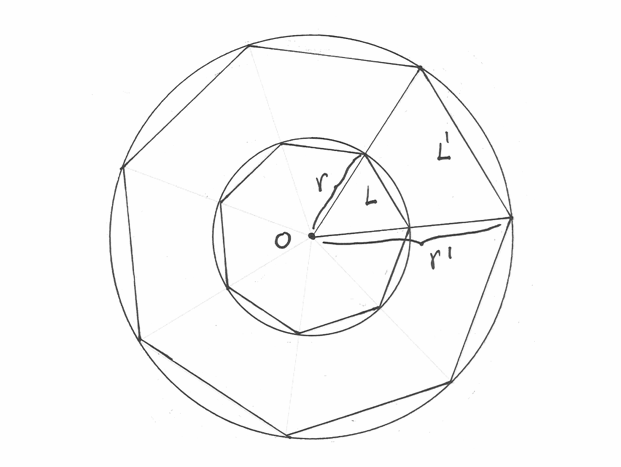
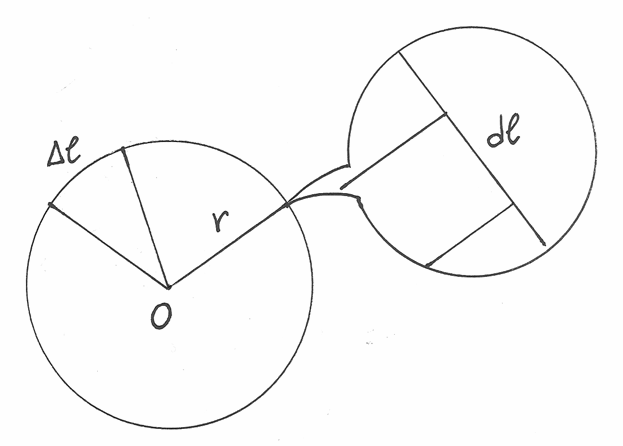
Disegniamo due circonferenze concentriche e un poligono di 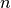 lati
inscritto in ciascuna in modo che i loro vertici siano allineati lungo i raggi .
Per ogni triangolo isoscele vale
lati
inscritto in ciascuna in modo che i loro vertici siano allineati lungo i raggi .
Per ogni triangolo isoscele vale 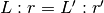 , cioè il rapporto fra
il lato e il raggio non cambia qualsiasi sia la circonferenza considerata.
Passando ai perimetri, si ha:
, cioè il rapporto fra
il lato e il raggio non cambia qualsiasi sia la circonferenza considerata.
Passando ai perimetri, si ha:
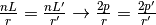
Supponiamo ora che il numero dei lati sia infinito (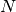 ). In questo
caso ogni lato è indistinguibile dall’arco di circonferenza corrispondente.
Allora il perimetro del poligono è indistinguibile dalla circonferenza
). In questo
caso ogni lato è indistinguibile dall’arco di circonferenza corrispondente.
Allora il perimetro del poligono è indistinguibile dalla circonferenza 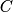 :
:
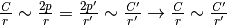
Il primo e l’ultimo termine di questa catena sono quindi indistinguibili.
Trattandosi di due numeri standard, abbiamo che i due rapporti sono uguali.
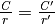 . Dato che questo rapporto
ha il medesimo valore per ogni circonferenza, gli si dà un nome particolare,
come sappiamo:
. Dato che questo rapporto
ha il medesimo valore per ogni circonferenza, gli si dà un nome particolare,
come sappiamo: 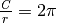 .
Come si vede, il ragionamento, che si sviluppa a partire
dal perimetro con infiniti lati, viene esteso alla circonferenza perché è
indistinguibile dal poligono di infiniti lati.
.
Come si vede, il ragionamento, che si sviluppa a partire
dal perimetro con infiniti lati, viene esteso alla circonferenza perché è
indistinguibile dal poligono di infiniti lati.
Ma vediamo di fare uso della definizione di integrale.
Fissiamo sulla circonferenza un punto iniziale 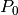 . A partire da questo
consideriamo gli
. A partire da questo
consideriamo gli 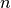 archi (orientati, per esempio, in senso antiorario) che
hanno per secondo estremo un altro punto
archi (orientati, per esempio, in senso antiorario) che
hanno per secondo estremo un altro punto 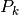 sulla circonferenza, con
sulla circonferenza, con
 che varia da
che varia da  a
a 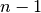 . I punti possono anche essere
distribuiti in modo irregolare. Definiamo la funzione
. I punti possono anche essere
distribuiti in modo irregolare. Definiamo la funzione 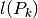 che calcola
la lunghezza di questi possibili archi. L’arco fra due punti successivi
che calcola
la lunghezza di questi possibili archi. L’arco fra due punti successivi
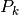 e
e 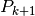 avrà per lunghezza la differenza
avrà per lunghezza la differenza
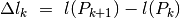 .
.
L’intera circonferenza è allora 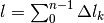 e poiché non
dipende dalla scelta dei punti nè dal loro numero, possiamo riscriverla come
e poiché non
dipende dalla scelta dei punti nè dal loro numero, possiamo riscriverla come
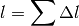
Non si tratta della primitiva di una successione, ma effettivamente di una somma, cioè del numero che fornisce la misura della circonferenza.
Se ora pensiamo che i punti di suddivisione siano infiniti (e quindi gli archi
siano infinitesimi), le differenze 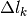 diventano differenziali
diventano differenziali
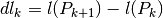 e la circonferenza risulterà dalla somma di
un numero infinito
e la circonferenza risulterà dalla somma di
un numero infinito 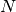 di queste differenze infinitesime:
di queste differenze infinitesime:
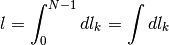
Anche in questo caso omettiamo gli indici perchè il risultato non dipende dal numero di punti, purché sia infinito, nè dalla misura dei singoli archi, purché siano infinitesimi. Non siamo però ancora in grado di dedurre il risultato del calcolo. Per arrivarci facciamo uso di una proprietà che sarà spiegata più avanti:
Se persi ha che
, allora anche
.
Quali sono i termini 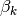 indistinguibili agli
indistinguibili agli 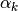 nel
nostro caso? Sono i lati del poligono di infiniti lati, indistinguibili dagli
archi infinitesimi corrispondenti sulla circonferenza circoscritta. Per questa
via si ricava il rapporto
nel
nostro caso? Sono i lati del poligono di infiniti lati, indistinguibili dagli
archi infinitesimi corrispondenti sulla circonferenza circoscritta. Per questa
via si ricava il rapporto 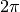 calcolato nelle righe precedenti e si ottiene
il risultato.
calcolato nelle righe precedenti e si ottiene
il risultato.
L’esempio illustra il ragionamento abituale in questo tipo di calcolo: in genere calcolare un integrale è difficile. Le difficoltà si superano riducendo il problema in parti infinitesime e riportandolo su altri infinitesimi, indistinguibili dai precedenti.
L’area del cerchio¶
Seguiamo il percorso precedente. Fissiamo un punto 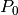 sulla circonferenza
e fissiamo gli altri punti in senso antiorario. Definiamo la funzione
sulla circonferenza
e fissiamo gli altri punti in senso antiorario. Definiamo la funzione 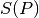 che associa a ogni punto
che associa a ogni punto 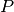 l’area del settore circolare
l’area del settore circolare 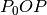 .
.
Immaginando 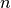 punti consecutivi
punti consecutivi 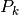 , da
, da 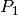 a
a 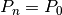 ,
avremo per il generico settore da
,
avremo per il generico settore da 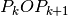 un’area data da
un’area data da
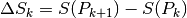 , per cui l’area del cerchio risulta
, per cui l’area del cerchio risulta
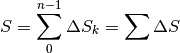
Come al solito, nell’ultima espressione omettiamo gli indici, perché la somma non dipende da questi, cioè non dipende dal numero dei punti e nemmeno dalla loro scelta.
Di nuovo, consideriamo che i punti siano infiniti e quindi che i settori
e le loro differenze siano gli infinitesimi 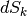 .
Allora l’area del cerchio è
.
Allora l’area del cerchio è
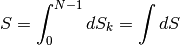
Ancora una volta, il ragionamento ci porta a spezzare il problema in una somma infinita di elementi infinitesimi, ma non è in grado di darci il risultato.
Il passaggio successivo è cercare l’area di una figura più semplice del settore circolare infinitesimo, indistinguibile da questo. La figura è il triangolo isoscele infinitesimo, che ha per lati due raggi e per base una corda infinitesima, indistinguibile dall’arco corrispondente. Possiamo allora riscrivere l’integrale inserendo la formula dell’area del triangolo
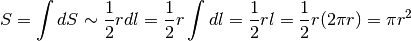
La catena di uguaglianze dice che il primo e l’ultimo termine sono numeri
indistinguibili. Poiché sono standard, saranno uguali: 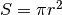
La superficie sferica¶
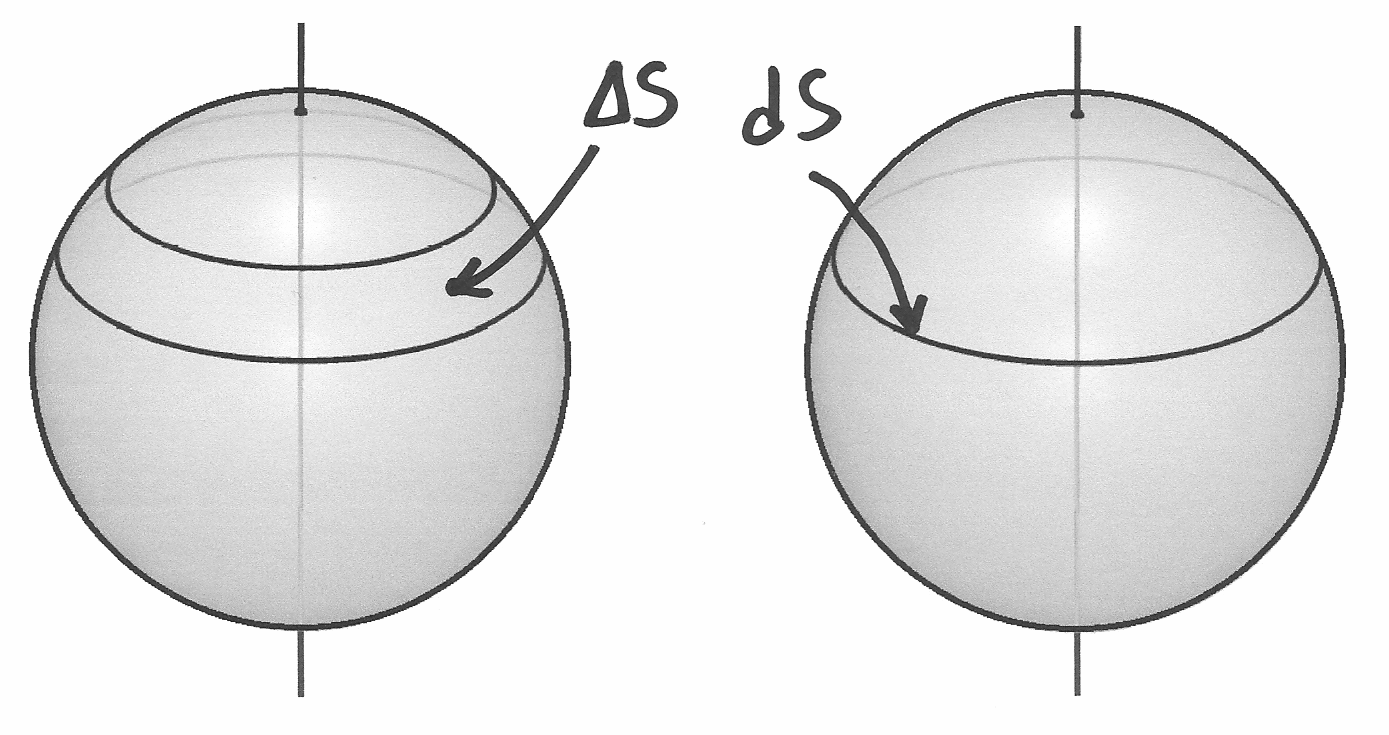
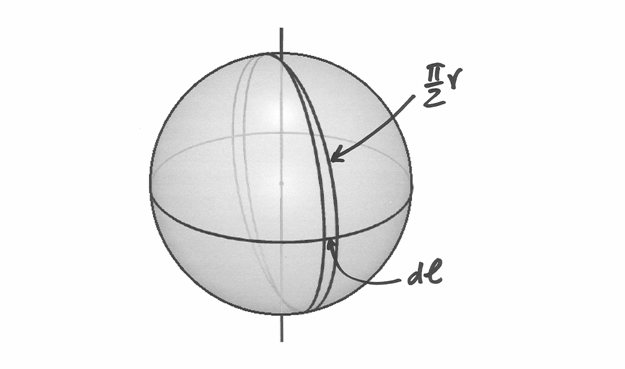
Immaginiamo di affettare una sfera perpendicolarmente ad un suo diametro, con
infiniti tagli paralleli, di spessore infinitesimo 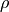 . La somma
infinita di tutti gli spessori è il diametro:
. La somma
infinita di tutti gli spessori è il diametro: 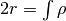 .
Ogni anello sferico ha superficie di area
.
Ogni anello sferico ha superficie di area 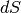 e l’integrale di tali
superfici costituisce la superficie sferica
e l’integrale di tali
superfici costituisce la superficie sferica 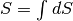 , il valore
che cerchiamo di calcolare.
, il valore
che cerchiamo di calcolare.
Come al solito, è difficile calcolare direttamente 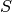 ed anche la sua
frazione infinitesima
ed anche la sua
frazione infinitesima 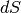 . Per questo cerchiamo una figura semplice,
di dimensioni infinitesime, indistinguibile da
. Per questo cerchiamo una figura semplice,
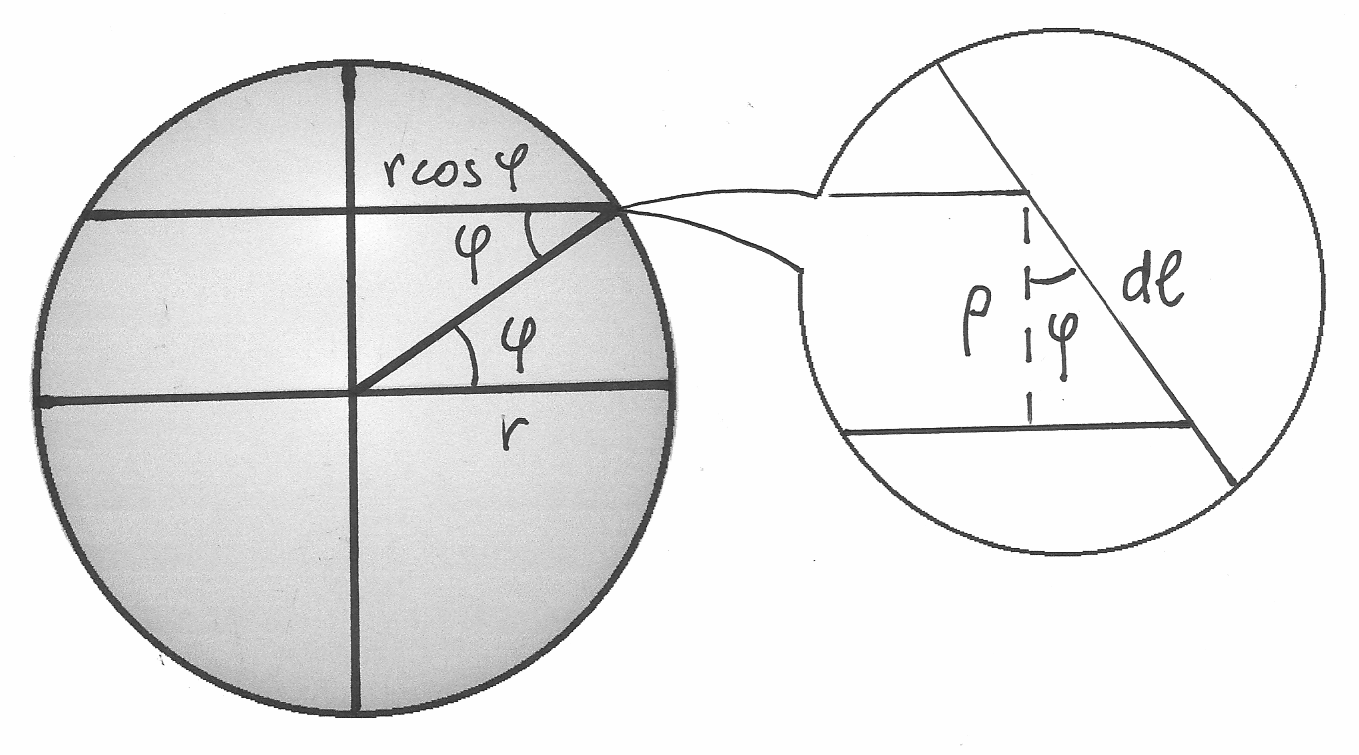
di dimensioni infinitesime, indistinguibile da 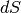 . Possiamo arrivarci
considerando che l’anello tagliato è indistinguibile da un rettangolo che ha
per base la circonferenza dell’anello e per altezza la sua larghezza.
Scriviamo allora le espressioni per questa circonferenza e per questa larghezza.
. Possiamo arrivarci
considerando che l’anello tagliato è indistinguibile da un rettangolo che ha
per base la circonferenza dell’anello e per altezza la sua larghezza.
Scriviamo allora le espressioni per questa circonferenza e per questa larghezza.
La circonferenza dipende dal suo raggio, che è massimo (uguale al raggio sferico
 ) se il taglio è equatoriale e progressivamente si riduce a zero
a seconda della latitudine
) se il taglio è equatoriale e progressivamente si riduce a zero
a seconda della latitudine 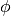 , l’angolo del raggio sferico che
tocca il taglio:
, l’angolo del raggio sferico che
tocca il taglio: 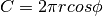 . La larghezza dipende anch’essa dalla
latitudine
. La larghezza dipende anch’essa dalla
latitudine 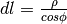 . Quindi
. Quindi
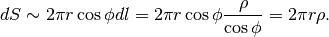
Questo consente di ottenere la superficie sferica:
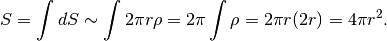
Note
 equivale a dire che la superficie sferica è
equivalente alla superficie laterale di un cilindro che ha lo stesso
raggio della sfera e l’altezza pari al suo diametro.
equivale a dire che la superficie sferica è
equivalente alla superficie laterale di un cilindro che ha lo stesso
raggio della sfera e l’altezza pari al suo diametro.
Una seconda soluzione ...sbagliata¶
Si potrebbe procedere in un altro modo: si potrebbe considerare la superficie sferica come l’insieme dei fusi, cioè delle figure curvilinee formate da due meridiani. La superficie racchiusa è l’unione di due triangoli curvilinei opposti, che hanno in comune un arco di equatore.
Se la misura di quest’arco è l’infinitesimo 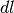 , allora l’area di un
fuso si potrebbe pensare indistinguibile dall’area di due
triangoli rettilinei che hanno per altezza mezzo meridiano:
, allora l’area di un
fuso si potrebbe pensare indistinguibile dall’area di due
triangoli rettilinei che hanno per altezza mezzo meridiano:
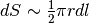 . L’area della superficie totale allora
sarebbe
. L’area della superficie totale allora
sarebbe
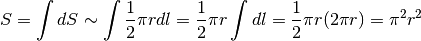
Come mai il risultato è diverso? L’errore sta nel dare per scontato che il mezzo
fuso sferico sia indistinguibile dal triangolo isoscele. Si può invece calcolare
e dimostrare che si tratta di due figure infinitesime, ma non indistinguibili, perché
non sono infinitesimi dello stesso ordine. In effetti il rapporto fra l’area del
triangolo sferico curvilineo e quella del triangolo isoscele corrispondente
vale  . Invece il primo metodo è corretto: infatti si può
calcolare che alle nostre latitudini, per esempio, due paralleli distanti
. Invece il primo metodo è corretto: infatti si può
calcolare che alle nostre latitudini, per esempio, due paralleli distanti
 hanno
una lunghezza diversa per circa
hanno
una lunghezza diversa per circa  (su
(su 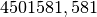 ). Quindi la
figura considerata non è esattamente un rettangolo, ma l’approssimazione
è eccellente. Le misure delle due basi hanno rapporto che non è
). Quindi la
figura considerata non è esattamente un rettangolo, ma l’approssimazione
è eccellente. Le misure delle due basi hanno rapporto che non è 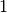 ,
ma
,
ma  .
.
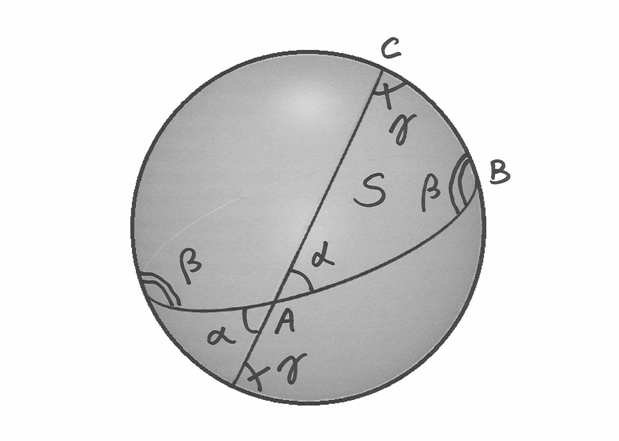
Il triangolo sferico¶
Il triangolo sferico generico ha per lati tre archi di cerchio massimo minori di una semicircoferenza.
Osservando la figura, cerchiamo l’area 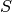 del triangolo
del triangolo  .
Consideriamo che l’equatore passi per
.
Consideriamo che l’equatore passi per 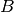 e
e 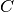 , allora il nostro
triangolo occupa una parte del fuso di ampiezza
, allora il nostro
triangolo occupa una parte del fuso di ampiezza 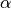 che si sviluppa
in due parti, opposte in
che si sviluppa
in due parti, opposte in 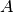 .
I fusi di ampiezza
.
I fusi di ampiezza 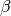 e
e 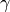 sono interamente contenuti
nell’emisfero visibile e comprendono anche il triangolo
sono interamente contenuti
nell’emisfero visibile e comprendono anche il triangolo 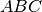 .
Un fuso generico, di ampiezza
.
Un fuso generico, di ampiezza 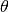 , occupa la frazione
, occupa la frazione
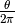 della superficie sferica, quindi ha area
della superficie sferica, quindi ha area
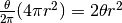 . L’area
. L’area 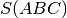 dell’emisfero visibile si ottiene dalla somma dei fusi, ma in questo
modo l’area del triangolo
dell’emisfero visibile si ottiene dalla somma dei fusi, ma in questo
modo l’area del triangolo 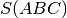 viene contata tre volte. Quindi:
viene contata tre volte. Quindi:
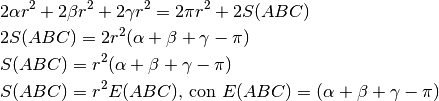
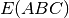 si chiama eccesso sferico. È la differenza fra la somma degli
angoli interni del triangolo sferico e la somma analoga di un comune triangolo.
Si può dire che l’area di un triangolo sferico è direttamente proporzionale al
suo eccesso sferico, attraverso il fattore
si chiama eccesso sferico. È la differenza fra la somma degli
angoli interni del triangolo sferico e la somma analoga di un comune triangolo.
Si può dire che l’area di un triangolo sferico è direttamente proporzionale al
suo eccesso sferico, attraverso il fattore 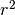 .
.
Nel problema 4.3.3 l’eccesso sferico è proprio l’angolo del fuso 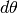 perché alla base del triangolo la somma degli angoli dà già
perché alla base del triangolo la somma degli angoli dà già 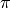 .
La seconda soluzione data al problema della superficie sferica considera
il triangolo sferico indistinguibile da un triangolo piano di base
.
La seconda soluzione data al problema della superficie sferica considera
il triangolo sferico indistinguibile da un triangolo piano di base
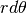 altezza
altezza 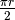 , quindi di area
, quindi di area
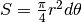 . Invece, se usiamo la formula del triangolo
sferico, la sua area è
. Invece, se usiamo la formula del triangolo
sferico, la sua area è 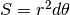 , quindi i due numeri
non sono indistinguibili.
, quindi i due numeri
non sono indistinguibili.
La calotta sferica e le stelle circumpolari¶
Dal fatto che la superficie sferica è equivalente a quella di un cilindro di pari
raggio e altezza uguale al diametro, si ricava che l’area della calotta sferica
di altezza 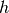 è
è 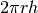
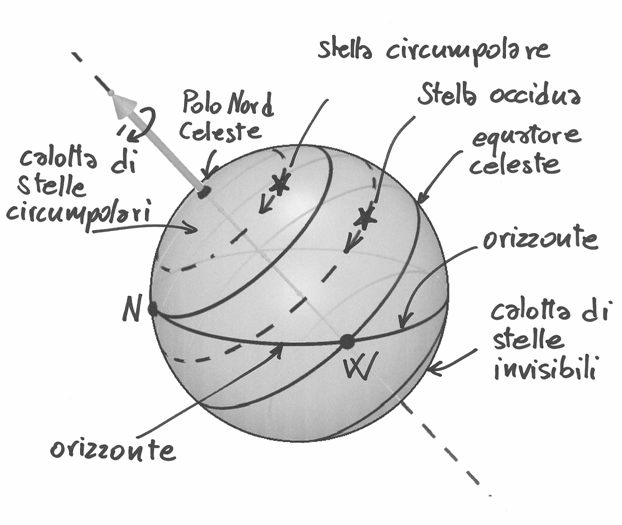
Chiamiamo circumpolari le stelle che possiamo vedere tutto l’anno sopra l’orizzonte.
Si trovano, per il nostro emisfero, attorno al Polo Nord Celeste (PNC), da cui il
loro nome. Da un oservatore sulla superficie terrestre, il PNC viene visto ad
un’altezza sull’orizzonte pari alla latitudine 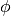 del luogo.
Calcoliamo, in base a questa, quale porzione di cielo stellato è sempre visibile.
del luogo.
Calcoliamo, in base a questa, quale porzione di cielo stellato è sempre visibile.
Chiamiamo  il raggio della sfera celeste, di area
il raggio della sfera celeste, di area 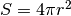 e cerchiamo l’area
e cerchiamo l’area 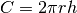 della calotta sferica delle stelle
circumpolari, che ha altezza
della calotta sferica delle stelle
circumpolari, che ha altezza 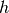 . Ricaviamo:
. Ricaviamo:
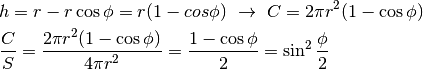
Le conseguenze sono, per esempio:
- al Polo Nord
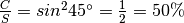 ,
, - all’Equatore, la latitudine è nulla, quindi...
- alla nostra latitudine,
per esempio
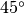 :
: 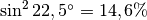
Le stelle che non sono circumpolari o sono invisibili oppure occidue. Le stelle visibili sono quelle circumpolari più quelle occidue e le stelle invisibili sono nella stessa percentuale di quelle circumpolari.
I volumi¶
Una generica superficie di base¶
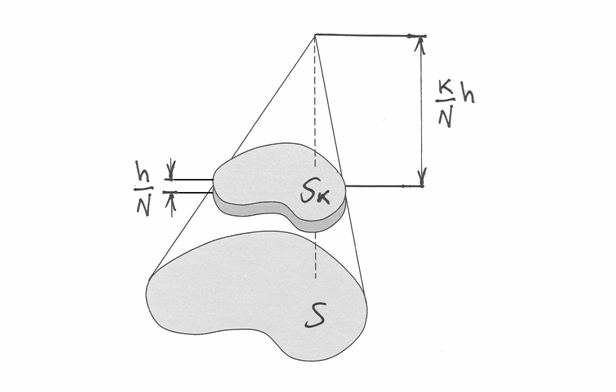
Nelle prossime figure sarà importante avere un metodo per cacolare l’area di una superficie generica, anche con contorno curvilineo.
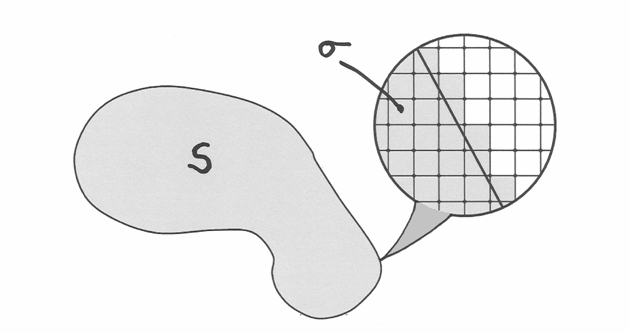
Una tecnica diffusa è quella di quadrettare l’area. Più la quadrettatura è fine, migliore è l’approssimazione. Con una quadrettatura di lato infinitesimo possiamo ottenere il risultato esatto. Alcuni quadretti saranno sul bordo della figura e comprendendoli nel calcolo commettiamo un errore che al massimo è dato dalla lunghezza del contorno per la diagonale di un quadretto, che è infinitesima. Si tratta quindi di un errore infinitesimo. Possiamo quindi scrivere
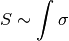
dove 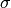 è l’area di un quadretto infinitesimo.
è l’area di un quadretto infinitesimo.
Il prisma e il cilindro¶
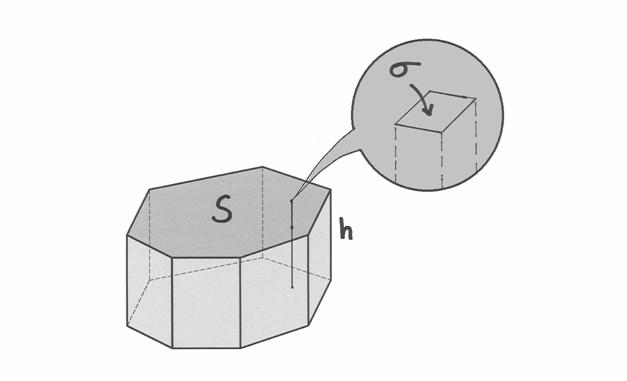
Risolto il problema della base, è semplice approssimare il volume di un prisma retto qualsiasi.
Basta immaginarlo composto di infiniti parallelepipedo con base quadrata, di
area infinitesima 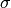 e altezza
e altezza 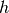 , quella del prisma.
Abbiamo che
, quella del prisma.
Abbiamo che
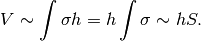
L’impostazione non cambia se la figura di base è curvilinea, cioè nel caso di un cilindro oppure di solido a base corvilinea generica
Il principio di Cavalieri¶
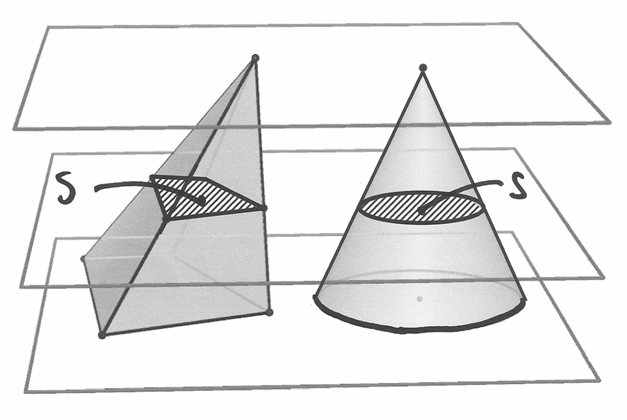
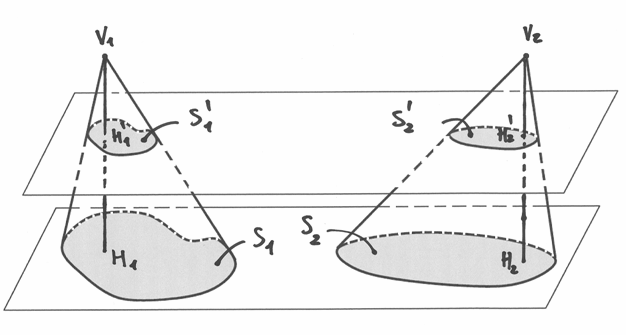
Se due solidi sono compresi fra due piani paralleli, primo e ultimo piano di un fascio che li interseca formando sezioni di area uguale, allora hanno lo stesso volume.
Immaginiamo che il fascio sia di infiniti piani a distanza infinitesima
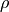 . Allora due piani successivi tagliano due scaglie
di spessore
. Allora due piani successivi tagliano due scaglie
di spessore 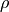 , di volume
, di volume 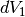 e
e 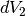 .
I volumi dei due solidi si ottengono quindi da:
.
I volumi dei due solidi si ottengono quindi da: 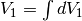 e
e
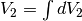 . Nel disegno si rappresenta uno spessore
piccolo, non infinitesimo, per evitare di complicare l’immagine
. Nel disegno si rappresenta uno spessore
piccolo, non infinitesimo, per evitare di complicare l’immagine
con i microscopi non standard. Le due scaglie dello stesso strato
hanno area uguale e volume indistinguibile: 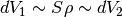
Proprietà di piramidi e coni¶
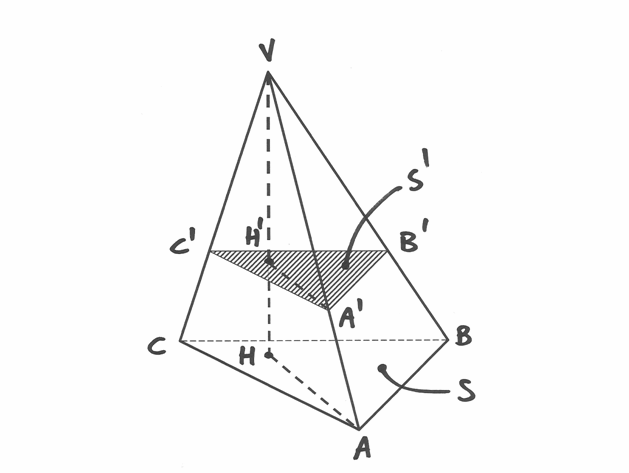
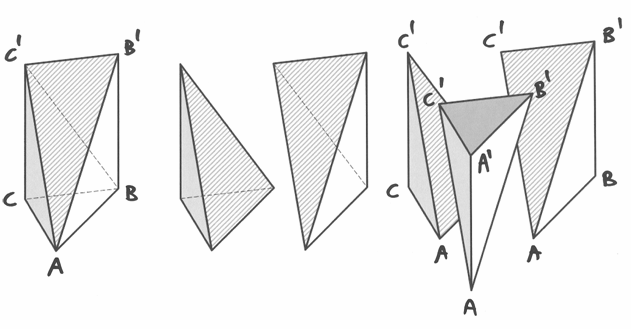
Anzitutto dimostriamo che in una piramide le sezioni parallele alla base sono simili alla base e sono proporzionali ai quadrati delle loro distanze dal vertice.
Consideriamo la sezione 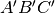 parallela
alla base: triangoli
parallela
alla base: triangoli 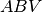 e
e 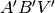 sono simili, dato che
sono simili, dato che 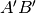 è parallelo a
è parallelo a 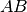 . Sono simili anche i triangoli rettangoli
. Sono simili anche i triangoli rettangoli 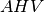 e
e
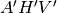 , che hanno per lato l’altezza della piramide. Quindi:
, che hanno per lato l’altezza della piramide. Quindi:
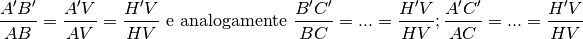
I due trangoli 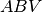 e
e 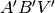 sono dunque simili. Ricordando che
le aree di due figure simili stanno nello stesso rapporto dei quadrati di due
lati omologhi, ricaviamo la seconda tesi:
sono dunque simili. Ricordando che
le aree di due figure simili stanno nello stesso rapporto dei quadrati di due
lati omologhi, ricaviamo la seconda tesi:
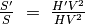 .
.
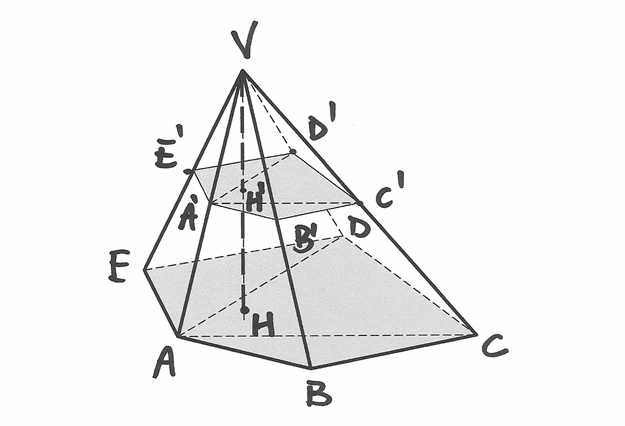
Questo risultato si estende a tutte le piramidi, perché qualsiasi base poligonale può essere divisa in triangoli (i dettagli della dimostrazione si lasciano per esercizio).
Possiamo anche estendere gli stessi risultati ai coni, cioè ai solidi con base curvilinea qualsiasi e con superficie laterale formata da infiniti segmenti che uniscono la base ad un unico punto, il vertice, esterno al piano della base.
Infatti possiamo pensare la base indistinguibile da un poligono di infiniti lati infinitesimi e ripetere per ognuno di essi la dimostrazione precedente.
Equivalenza fra coni¶
Due coni con le basi equivalenti e uguale altezza hanno lo stesso volume.
Basiamo la dimostrazione sul principio di Cavalieri. Consideriamo un piano
intermedio e le due sezioni 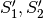 . Poiché le due altezze sono
uguali, allora sono uguali anche le distanze del piano dai due vertici:
. Poiché le due altezze sono
uguali, allora sono uguali anche le distanze del piano dai due vertici:
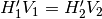 .
.
Abbiamo che:
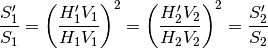
che ha per conseguenza che 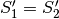 perchè le due aree di base
sono uguali per ipotesi.
Questo comporta che per il principio di Cavalieri i due volumi sono uguali.
perchè le due aree di base
sono uguali per ipotesi.
Questo comporta che per il principio di Cavalieri i due volumi sono uguali.
Note
Si dimostra la stessa tesi applicando le stesse ipotesi a due piramidi.
Il volume di piramidi e coni¶
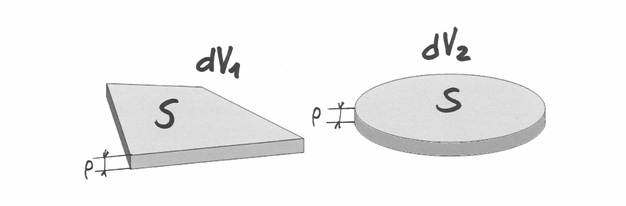
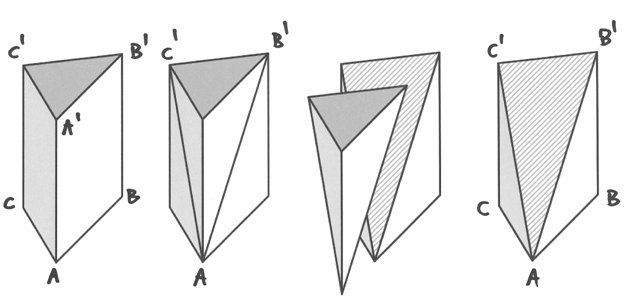
I disegni mostrano la scomposizione di un prisma in tre piramidi che hanno lo
stesso volume perché di uguali basi e altezze (per l’ultima si considera come base
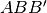 , equiestesa rispetto a
, equiestesa rispetto a 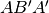 ).
).
Da ragionamenti come questo viene la regola per il volune di una piramide:
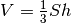 . Per le analogie che abbiamo già visto, la stessa
formula si estende anche al volume dei coni.
. Per le analogie che abbiamo già visto, la stessa
formula si estende anche al volume dei coni.
Un secondo modo per il cono¶
Ricaviamo nuovamente la formula del volume del cono, facendo uso, questa volta, del calcolo integrale.
Un cono con area di base 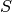 e altezza
e altezza 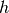 viene tagliato in un numero
infinito
viene tagliato in un numero
infinito 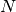 di scaglie parallele alla base, di spessore infinitesimo
di scaglie parallele alla base, di spessore infinitesimo 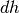 .
Per quanto visto nel par.4, per la
.
Per quanto visto nel par.4, per la 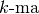 sezione, che si trova a
distanza
sezione, che si trova a
distanza 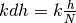 dal vertice, vale:
dal vertice, vale:
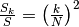 , e quindi:
, e quindi:
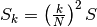 . Allora il volume del
. Allora il volume del 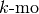 strato è
strato è
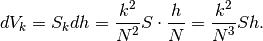
e il volume del cono
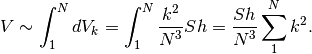
Nell’ultima formula la somma sostituisce l’integrale perché  lasciato
solo sotto il segno di integrale, non è un infinitesimo (anzi assume anche
valori infiniti). Proseguendo, ricordiamo
che
lasciato
solo sotto il segno di integrale, non è un infinitesimo (anzi assume anche
valori infiniti). Proseguendo, ricordiamo
che 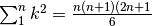 e ricaviamo:
e ricaviamo:
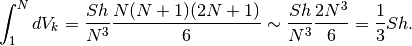
Il volume di una sfera¶
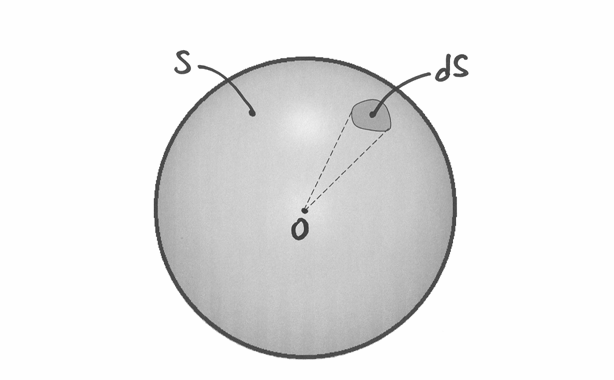
Isoliamo sulla superficie di una sfera una superficie infinitesima 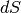 e immaginiamo che sia la base di un cono con vertice nel centro della sfera.
Il volume del cono infinitesimo è
e immaginiamo che sia la base di un cono con vertice nel centro della sfera.
Il volume del cono infinitesimo è 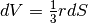 . E il volume della sfera:
. E il volume della sfera:
Un secondo modo per la sfera¶
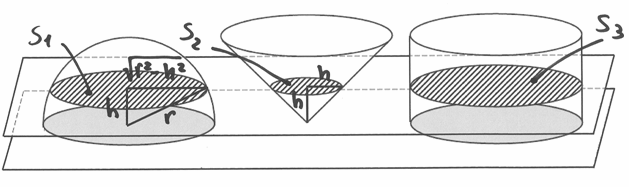
Il prossimo disegno confronta una semisfera, un cono rovesciato ed un cilindro,
tutti con raggio  e altezza uguale al raggio, appoggiati sullo stesso
piano e tagliati da un piano parallelo ad altezza
e altezza uguale al raggio, appoggiati sullo stesso
piano e tagliati da un piano parallelo ad altezza  . Le sezioni che il
piano individua nelle tre figure sono diverse. Il raggio della sezione
. Le sezioni che il
piano individua nelle tre figure sono diverse. Il raggio della sezione  della sfera è dato da
della sfera è dato da 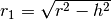 . Il raggio della sezione
. Il raggio della sezione
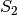 del cono è
del cono è 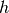 , mentre il raggio della sezione
, mentre il raggio della sezione 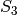 è
è  . Possiamo confrontare le aree di queste tre sezioni:
. Possiamo confrontare le aree di queste tre sezioni:
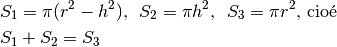
Dal principio di Cavalieri segue che il volume del cilindro è eguaglia la somma
dei volumi della semisfera e del cono. Per il cilindro 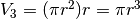 ,
per il cono
,
per il cono 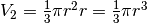 . Così il volume
della semisfera vale:
. Così il volume
della semisfera vale:
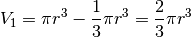
e quindi, raddoppiando, si ottiene il volume della sfera.
Riassunto¶
- Le primitive
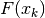 di una funzione
di una funzione 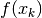 a dominio discreto
sono le funzioni che hanno rapporto incrementale
a dominio discreto
sono le funzioni che hanno rapporto incrementale 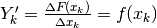 uguale alla funzione data.
uguale alla funzione data. - L’espressione per una generica primitiva è:
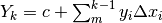 .
I suoi valori si ricavano come somme a partire da una costante iniziale
.
I suoi valori si ricavano come somme a partire da una costante iniziale
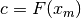 .
. - Ricavare queste primitive ha per analogo geometrico ricostruire una spezzata a partire da un punto iniziale e dalle pendenze dei suoi segmenti.
- L’espressione delle somme ha anche il significato dell’area totale di un
polirettangolo, le cui basi sono i vari
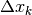 e le cui altezze
sono date dai valori
e le cui altezze
sono date dai valori 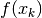 .
. - L’integrale è la somma di un numero ipernaturale
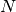 di infiniti
infinitesimi
di infiniti
infinitesimi 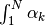 , dove il simbolo
, dove il simbolo 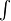 sta per somma.
Il tipo di tale somma non è a priori determinabile.
sta per somma.
Il tipo di tale somma non è a priori determinabile. - Come esempio di applicazione, vengono ricavate molte formule di uso comune in geometria: per la circonferenza e l’area del cerchio, per l’area della superficie sferica, del triangolo sferico e dalla calotta, per i volumi di vari solidi.
- Il principio di Cavalieri assicura che hanno pari volume due solidi che, sezionati da piani paralleli alle due rispettive basi, hanno sezioni corrispondenti di uguale area.
Esercizi¶
- Seguendo il calcolo dell’esempio 4.3.3 calcola l’area della superficie di una
calotta sferica di raggio
 e altezza
e altezza 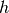 .
. - Completa la dimostrazione relativa alle piramidi con base qualsiasi, della quale hai il disegno nel par.4.4.4.
- Calcola quale percentuale di stelle circumpolari occupa il cielo visibile
alla nostra latitudine ed esprimi poi questo rapporto in funzione di
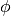 .
.