Il teorema fondamentale e le sue conseguenze¶
Come abbiamo visto nel capitolo precedente, calcolare le somme è troppo oneroso e quindi rinunciamo a calcolare le primitive attraverso le somme. Se troviamo un altro modo di calcolare le primitive, ci avvarremo di questo nuovo modo per il calcolo delle somme.
Il teorema fondamentale¶
Supponiamo di avere una successione 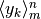 e di conoscere
le primitive
e di conoscere
le primitive 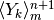 . Allora la k_esima primitiva è
. Allora la k_esima primitiva è
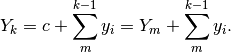
Quindi, riscrivendo l’ultimo termine 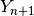 si ha:
si ha:
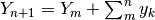 , cioè:
, cioè:
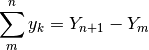
Questa è la formulazione del cosiddetto teorema fondamentale del calcolo delle somme: per calcolare la somma di una successione basta sottrarre la primitiva relativa al suo primo termine dalla primitiva relativa al termine successivo rispetto al suo ultimo.
Per comodità di scrittura si usa porre ![Y_n-Y_m=\left[Y_k\right]_m^n](../../../_images/math/643f610565283aa3141dfe704361e36514aaa797.png) ,
cioè la differenza si sintetizza con un’espressione fra parentesi quadre e
i due indici associati. Per esempio
,
cioè la differenza si sintetizza con un’espressione fra parentesi quadre e
i due indici associati. Per esempio ![\left[k^2\right]_3^7=7^2-3^2=40](../../../_images/math/c65241b1a81346b20912b601ad4c62e20250b943.png) .
Adeguandoci a questo uso, scriviamo:
.
Adeguandoci a questo uso, scriviamo:
![\sum_m^n y_k=\left[Y\right]_m^{n+1}.](../../../_images/math/84dc6627cb6d71299fec1528984f20c6cc3d22f2.png)
Siamo ora tornati al problema di come calcolare le primitive.
Dalle primitive alle somme¶
Abbiamo individuato nelle primitive la soluzione del problema che ci eravamo posti all’inizio del capitolo precedente: a partire da una successione di differenze, ricostruire quale successione ne poteva essere l’origine. I vari ragionamenti ci hanno portato a cercare le primitive calcolando le somme, un calcolo che però si è rivelato difficile. Siamo quindi al punto di dover calcolare le primitive per altra via.
Successione di potenze¶
Ragioniamo usando le espressioni conosciute delle differenze. Per esempio
sappiamo che 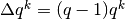 . Quindi se la differenza
. Quindi se la differenza 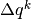 ha questo risultato, vuol dire che
ha questo risultato, vuol dire che 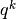 è primitiva di
è primitiva di 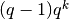 .
Di per sè non è un’informazione molto richiesta, nel senso che la successione
.
Di per sè non è un’informazione molto richiesta, nel senso che la successione
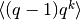 non è particolarmente interessante, però ci è utile
il ragionamento. Dividendo per
non è particolarmente interessante, però ci è utile
il ragionamento. Dividendo per 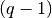 si ha:
si ha:
![\Delta\left[\frac{q^k}{q-1}\right]=\frac{1}{q-1}(q-1)q^k=q^k.](../../../_images/math/c2aa371d8a7ef0995b608779d4bc62e6fde0d100.png)
Se la differenza a sinistra è uguale a 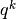 , allora una generica primitiva
di
, allora una generica primitiva
di 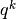 è
è 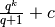 .
.
Nel capitolo precedente (Par.2.6.1) ci siamo
trovati a dover calcolare 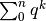 e ce la siamo cavata con qualche
artificio algebrico. Ora possiamo farlo usando il teorema fondamentale:
e ce la siamo cavata con qualche
artificio algebrico. Ora possiamo farlo usando il teorema fondamentale:
![\sum_0^nq^k=\left[\frac{q^k}{q-1}\right]_0^{n+1}=\frac{q^{n+1}}{q-1}-\frac{q^0}{q-1}=\frac{q^{n+1}-1}{q-1}.](../../../_images/math/9c7e1502078ed0c4d93ea8aea186d63765412bc5.png)
che è il risultato già trovato, ma questa volta in modo molto più rapido.
Fattoriali decrescenti e somma di n numeri¶
Abbiamo già visto che 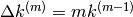 . Da questo sappiamo che
. Da questo sappiamo che
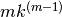 ha per primitiva
ha per primitiva 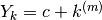 . Ancora una volta abbiamo
la primitiva di una funzione poco interessante. Allora modifichiamo leggermente
la primitiva e calcoliamo la differenza:
. Ancora una volta abbiamo
la primitiva di una funzione poco interessante. Allora modifichiamo leggermente
la primitiva e calcoliamo la differenza:
![\Delta \left[c+\frac{k^{(m+1)}}{m+1}\right]= \frac{1}{m+1}(m+1)k^{(m)}=k^{(m)}.](../../../_images/math/b4ef66963b15bd9c9abe505362e8d03c09e7b666.png)
In questo modo riconosciamo che la primitiva generica di 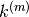 è
è 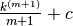 .
.
Il risultato è utile per esempio per calcolare la somma di n naturali
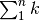 . Dato che
. Dato che 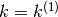 , una sua primitiva è
, una sua primitiva è
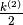 . Usiamo allora il teorema fondamentale:
. Usiamo allora il teorema fondamentale:
![\sum_1^nk=\left[\frac{k^{(2)}}{2}\right]_1^{n+1}=\frac{(n+1)^{(2)}}{2}-\frac{1^{(2)}}{2}=\frac{n(n+1)}{2}.](../../../_images/math/a786bcf3a2fd3a36ea2ff5461411f7b8663d6d98.png)
Ed è un modo ulteriore per ricavare questo risultato, che conoscevamo già.
Regole di calcolo¶
Direttamente dalle proprietà (di linearità) delle somme, possiamo ricavare:
- Le primitive della somma di due successioni sono le somme delle primitive delle due successioni.
Infatti se 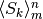 è la primitiva di
è la primitiva di 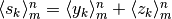 , allora deve essere:
, allora deve essere:
![S_k=c+\sum_m^{k-1}[y_i+z_i]=\left(c_1+\sum_m^{k-1}y_i\right)+\left(c_2+\sum_m^{k-1}z_i\right)=Y_k+Z_k,](../../../_images/math/79f44d7115bd706f66d7d05238091944d40a464a.png)
in cui abbiamo inteso che 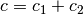 .
.
- Le primitive del prodotto di una costante per una successione sono i prodotti della costante per le primitive della successione.
Infatti se 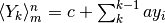 è la primitiva di
è la primitiva di
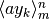 , allora deve essere:
, allora deve essere:
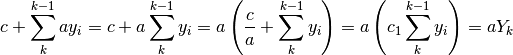
Quale simbolo per la primitiva?¶
Invece del generico simbolo 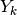 , per indicare le primitive di una
successione si usa il simbolo di somma
, per indicare le primitive di una
successione si usa il simbolo di somma  , in un modo leggermente diverso da
quello che si usa per le somme. La ragione di questo duplice uso è che le
proprietà delle primitive, come abbiamo visto, sono legate alle proprietà
delle somme. Per cui invece di
, in un modo leggermente diverso da
quello che si usa per le somme. La ragione di questo duplice uso è che le
proprietà delle primitive, come abbiamo visto, sono legate alle proprietà
delle somme. Per cui invece di 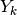 scriveremo
scriveremo 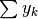 .
.
Note
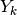 è la successione primitiva della successione
è la successione primitiva della successione 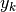 , quindi
il simbolo
, quindi
il simbolo 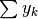 indica una successione, non una somma. Per segnalare
la diversità rispetto a una vera somma si evita di indicare gli estremi
indica una successione, non una somma. Per segnalare
la diversità rispetto a una vera somma si evita di indicare gli estremi  fra i quali varia l’indice
fra i quali varia l’indice  . Non si tratta solo di una notazione diversa,
perché la differenza è sostanziale: la somma
. Non si tratta solo di una notazione diversa,
perché la differenza è sostanziale: la somma 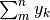 è un numero, mentre la primitiva
è un numero, mentre la primitiva 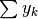 è una successione.
è una successione.
Le proprietà del paragrafo precedente, allora si possono esprimere così:
![1) \sum [y_k \pm z_k]&= \sum y_k \pm \sum z_k\\
2) \sum ay_k&= a\sum y_k](../../../_images/math/bb88963823ea604010322c2e9b26d0ab09e14c6e.png)
E le formule ricavate in precedenza sono:
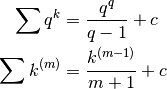
Il teorema fondamentale del calcolo delle somme allora si esprime così:
![\sum_m^n y_k=\left[\sum y_k\right]_m^{n+1}.](../../../_images/math/1c0639ab76180a24bde0d4e8e3abd6725b363293.png)
La regola che manca¶
Guardando la regola 1 viene spontaneo estenderla anche al prodotto e al quoziente: insomma sarebbe carino se il prodotto di due successioni avesse per primitiva il prodotto delle due primitive (e così anche il quoziente). Invece questo non vale, infatti:
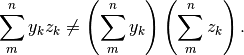
Limitiamoci ad un esempio con due soli termini, così risulta più evidente:
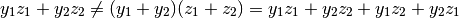
Proprio per questo è così difficile il calcolo delle somme, perché manca una
regola semplice sul prodotto. Tuttavia abbiamo una regola che in diversi casi
fa fronte alle difficoltà, per esempio ci aiuta nella ricerca della primitiva di
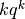 , che altrimenti sarebbe molto difficile.
, che altrimenti sarebbe molto difficile.
La somma per parti¶
Partiamo dalla differenza di un prodotto. Come sappiamo:
![\Delta[y_kz_k]=\Delta y_kz_{k+1}+y_k\Delta z_k](../../../_images/math/f918733c605b7281dca58f21bb47a8af1993e56a.png) .
Da questo si ricava che
.
Da questo si ricava che 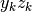 è una primitiva per la differenza, a meno
di una costante:
è una primitiva per la differenza, a meno
di una costante:
![(*) \sum\left[\Delta y_kz_{k+1}+y_k\Delta z_k\right]=y_kz_k+c](../../../_images/math/4e562484b99804a953b65f957d1a8c9414d2f2b1.png)
Applichiamo le proprietà in modo da rendere utile l’uguaglianza
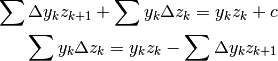
Anche se non è semplice, questa formula è l’unica che abbiamo per cercare la primitiva di un prodotto e funziona bene in un buon numero di casi, anche se non in tutti. La formula si chiama somma indefinita per parti.
Applichiamo il teorema fondamentale alla formula (*) :
![&\sum_m^n\left[\Delta y_kz_{k+1}+y_k\Delta z_k\right]=\left[y_kz_k\right]_m^{n+1} \\
&\sum_m^n\Delta y_kz_{k+1}+\sum_m^n y_k\Delta z_k=\left[y_kz_k\right]_m^{n+1} \\
&\sum_m^n y_k\Delta z_k=\left[y_kz_k\right]_m^{n+1}-\sum_m^n\Delta y_kz_{k+1}](../../../_images/math/8eaebaced1c6790ce04142383613919d4c66c61c.png)
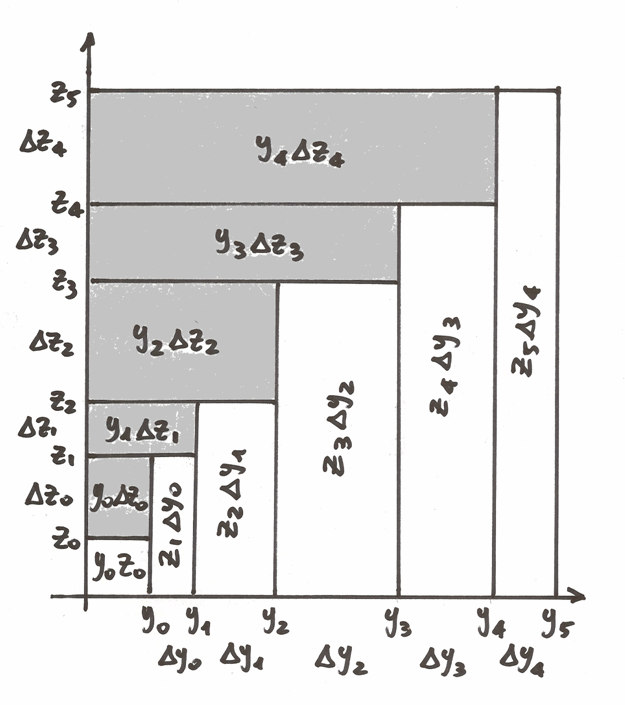
L’ultima formula è detta somma definita per parti. Possiamo renderla più
chiara con un esempio geometrico, in cui  .
.
![\sum_0^4 y_k\Delta z_k=\left[y_kz_k\right]_0^5-\sum_0^4\Delta y_kz_{k+1}](../../../_images/math/61dfc5baa289ba7a43ff2e865362f714bd8b6ae5.png)
cioé:
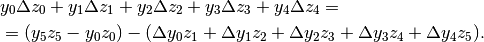
In questa figura abbiamo immaginato che i termini delle successioni siano
positivi e le successioni siano crescenti. I termini di 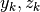 sono
allineati lungo gli assi cartesiani. L’area colorata a sinistra è una figura a
gradini e vale quanto la prima riga della formula precedente. Nella seconda riga
di questa formula, la stessa area è rappresentata come differenza fra l’intera
figura, tranne il rettangolino minore con vertice nell’origine, e i vari gradini
più chiari.
sono
allineati lungo gli assi cartesiani. L’area colorata a sinistra è una figura a
gradini e vale quanto la prima riga della formula precedente. Nella seconda riga
di questa formula, la stessa area è rappresentata come differenza fra l’intera
figura, tranne il rettangolino minore con vertice nell’origine, e i vari gradini
più chiari.
Esempi di calcolo¶
Somme di n quadrati¶
A partire da questi primi risultati possiamo ottenerne altri. Per esempio ricalcoliamo
la somma dei quadrati con la nuova notazione e con il teorema fondamentale.
Poiché questo ci porta cercare 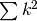 , che per noi è difficoltoso, possiamo
riscrivere
, che per noi è difficoltoso, possiamo
riscrivere 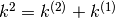 perché
perché 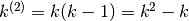 . Quindi
. Quindi
![\sum k^2=\sum\left[k^{(2)}+k^{(1)}\right]=\sum k^{(2)}+\sum k^{(1)}=
\frac{k^{(3)}}{3}+\frac{k^{(2)}}{2}+c.](../../../_images/math/43cf0650bb5c9abbf6cb2ce78ba281339a76f9ad.png)
ora applichiamo il teorema fondamentale:
![\sum k^2 &=\sum\left[\frac{k^{(3)}}{3}+\frac{k^{(2)}}{2}\right]_1^{n+1}=\frac{(n+1)^{(3)}}{3}+\frac{(n+1)^{(2)}}{2}-\frac{1^{(3)}}{3}-\frac{1^{(2)}}{2}=...=\\
&=\frac{n(n+1)(2n+1)}{6}.](../../../_images/math/0d37d7dc2358139ac97ac335000f2baa20f10964.png)
Somme di n cubi¶
Anche in questo caso sfruttiamo i fattoriali decrescenti, dato che conosciamo la
regola sulle loro somme: 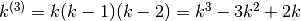 . D’altra parte
. D’altra parte
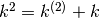 , per cui si ottiene:
, per cui si ottiene:
![k^3=k^{(3)} +3[k^{(2)}+k]-2k=k^{(3)}+3k^{(2)}+k=k^{(3)}+3k^{(2)}+k^{(1)}.](../../../_images/math/ce4accd10e09bb063a0ac256ec9d09ad7049c462.png)
Il completamento viene lasciato per esercizio.
I numeri di Stirling¶
Vediamo se è possibile esprimere qualsiasi potenza in termini di fattoriali decrescenti. Finora i risultati sono stati questi:
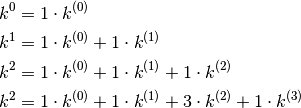
A parte gli esponenti, i coefficienti sono distribuiti in questo modo:
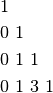
Questa specie di triangolo, che ricorda il Triangolo di Tartaglia, costituisce
l’elenco (iniziale) dei numeri di Stirling di seconda specie 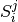 .
Servono appunto per indicare i coefficienti dei fattoriali decrescenti con cui
esprimere le potenze. Per avere un elenco più completo, si può fare una ricerca
in rete. Si troverà per esempio che per
.
Servono appunto per indicare i coefficienti dei fattoriali decrescenti con cui
esprimere le potenze. Per avere un elenco più completo, si può fare una ricerca
in rete. Si troverà per esempio che per 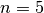 si ha
si ha
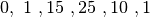 per cui
per cui
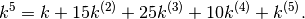
Una somma per parti¶
Impariamo l’applicazione della regola della somma per parti cercando la primitiva di
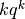 . Questa è la formula:
. Questa è la formula:
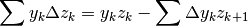
Al primo membro c’è il prodotto fra una successione e la differenza di un’altra.
Il fattore 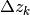 è una successione da leggere come fosse la
differenza di un’altra. Dobbiamo scegliere questo termine con saggezza: dobbiamo
essere in grado di scrivere la sua primitiva. Al secondo membro compare
poi una somma indefinita, che costituisce l’ostacolo maggiore.
è una successione da leggere come fosse la
differenza di un’altra. Dobbiamo scegliere questo termine con saggezza: dobbiamo
essere in grado di scrivere la sua primitiva. Al secondo membro compare
poi una somma indefinita, che costituisce l’ostacolo maggiore.
Dunque, cerchiamo di determinare 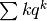 . Fra i due fattori,
. Fra i due fattori,  e
e 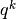 , quale può essere pensato come differenza di un’altra successione?
In realtà, entrambi. Proviamo quindi con il più facile:
, quale può essere pensato come differenza di un’altra successione?
In realtà, entrambi. Proviamo quindi con il più facile:  .
.
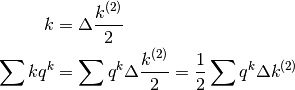
Per il momento trascuriamo  e applichiamo la formula della
somma per parti:
e applichiamo la formula della
somma per parti:
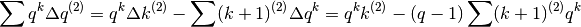
Purtroppo l’ultima somma è ancora più difficile dell’esercizio di partenza, per
cui dobbiamo cambiare strada. Questa volta puntiamo su 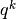 .
.
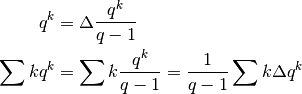
Applichiamo la formula della somma per parti all’ultima somma:
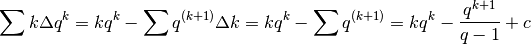
quindi, ricapitolando:
![\sum kq^k &=\frac{1}{q-1}\sum k\Delta q^k=\frac{1}{q-1}\left[kq^k-\sum q^{(k+1)}\Delta k\right]=\\
&=\frac{1}{q-1}\left[kq^k-\frac{q^{k+1}}{q-1}\right]=\frac{(k-1)q^{k+1}-kq^k}{(k-1)^2}](../../../_images/math/e460a7be66c2f92201fe633270d511add8082430.png)
Possiamo ora applicare il teorema fondamentale per calcolare la somma dei primi n termini e con pochi passaggi troviamo il risultato già calcolato al termine del Cap.2.
Somme con i numeri di Fibonacci¶
I numeri di Fibonacci formano la successione: 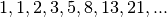 secondo la regola
secondo la regola 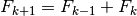 : ogni termine, tranne i primi due
che valgono
: ogni termine, tranne i primi due
che valgono 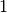 , è la somma dei due precedenti. Poniamo che il primo indice
sia
, è la somma dei due precedenti. Poniamo che il primo indice
sia 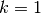 , così che
, così che 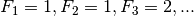 e calcoliamo la somma
e calcoliamo la somma
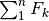 .
.
Somma dei numeri di Fibonacci¶
Un primo risultato si può ottenere per tentativi: la successione delle somme
risulta 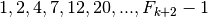 : la somma di indice
: la somma di indice  si ricava direttamente dalla successione, sottraendo
si ricava direttamente dalla successione, sottraendo 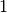 al
il termine di posto
al
il termine di posto 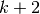 .
.
Note
Questa regola è empirica, ma si può dimostrare
per induzione. La base dell’induzione è 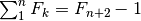 .
L’ereditarietà è
.
L’ereditarietà è 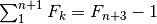 . Questo è vero perché
. Questo è vero perché
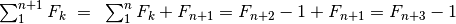 .
.
Supponiamo di non conoscere il risultato e ripartiamo dalla definizione:
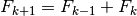 . Da questa deriva:
. Da questa deriva:
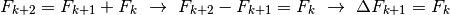
Risulta quindi che 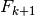 è una primitiva per
è una primitiva per 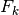 e possiamo
applicare il teorema fondamentale del calcolo delle somme:
e possiamo
applicare il teorema fondamentale del calcolo delle somme:
![\sum_1^nF_k=\left [F_{k+1}\right]_1^{n+1}=F_{n+2}-F_2=F_{n+2}-1.](../../../_images/math/9f7052d6327fb03dafea740e091a253622922c2b.png)
Somma dei numeri di Fibonacci moltiplicati pe i loroi indici¶
Proviamo a calcolare 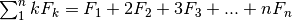 .
.
Dall’esempio precedente sappiamo che 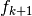 è la primitiva di
è la primitiva di 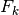 .
Allora, usando la somma definita per parti,
.
Allora, usando la somma definita per parti,
![&\sum_1^n kF_k=\sum_1^nk\Delta F_{k+1}=\left[kF_{k+1}\right]_1^{n+1}-
\sum_1^nF_{k+2}\Delta k=\\
&=(n+1)F_{n+2}-F_2-\sum_1^nF_{k+2}=(n+1)F_{n+2}-1-\sum_3^{n+2}F_k=\\
&=(n+1)F_{n+2}-1-\left[F_{k+1}\right]_3^{n+3}=(n+1)F_{n+2}-1-(F_{n+4}-F_4)=\\
&=(n+1)F_{n+2}-1-F_{n+4}+3=(n+1)F_{n+2}-F_{n+4}+2=\\
&=(n+1)F_{n+2}-(F_{n+2}+F_{n+3})+2=nF_{n+2}-F_{n+3}+2.](../../../_images/math/b6a2a226db839323ea8161131a2aa5b6ddccbf86.png)
Per esempio, per 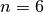 abbiamo
abbiamo 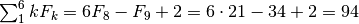 .
.
Riassunto¶
- Il teorema fondamentale del calcolo delle somme dice che la somma di una successione si ottiene svolgendo la differenza fra la primitiva del termine successivo all’ultimo e la primitiva del suo primo termine.
- Il teorema ci consente il calcolo delle somme, purché si sappiano calcolare le primitive.
- Le primitive vengono calcolate rovesciando i ragionamenti già conosciuti sulle differenze: se si riconosce che una successione è la differenza di un’altra, allora quest’ultima è la sua primitiva, a meno di una costante.
- Per lo stretto legame esistente fra somme e primitive, il simbolo di primitiva è uguale al simbolo di somma, senza indici.
- Se una successione è data dalla somma di due successioni, allora le sue primitive si ricavano dalle somme delle sue primitive.
- Se una successione ha tutti i termini moltiplicati per una costante, allora i termini delle sue primitive saranno tutti moltiplicati per la stessa costante.
- Non c’è una regola sul prodotto fra due successioni, analoga alla regola della somma. Esiste una regola sul prodotto alquanto laboriosa ma utile in molti casi: la regola della somma per parti.
- I numeri di Stirling di seconda specie forniscono i coefficienti per sviluppare la potenza di un numero in termini dei suoi fattoriali decrescenti.
Esercizi¶
- Dimostra la Regola di calcolo 1, partendo dal risultato. Metti in evidenza le ipotesi prima di procedere.
- Dimostra la Regola di calcolo 2, partendo dal risultato. Metti in evidenza le ipotesi prima di procedere.
- Calcola la somma dei primi n numeri dispari, seguendo le regole del paragrafo 3.5.
- Concludi l’esercizio della somma di n cubi, come iniziato nel sottoparagrafo 3.5.2.
- Usando i numeri di Stirling di seconda specie, sviluppa
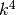 e calcola
e calcola
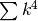 .
. - Concludi l’ultimo esempio del capitolo, esplicitando i calcoli.
- Concludi il paragrafo 3.6.3, questa volta a partire dalla somma definita per parti.