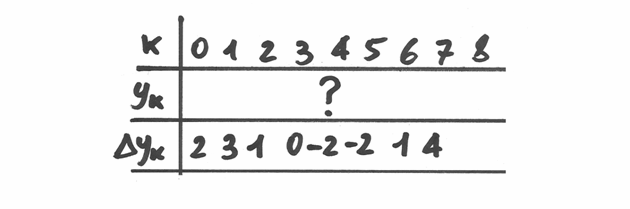Dalle differenze alle somme¶
Premessa¶
Il nostro viaggio nel calcolo integrale inizia con le successioni, più precisamente con il tentativo di ricostruire i termini di una successione, a partire dal suo tasso di variazione.
Il secondo passo, nei capitoli successivi, sarà quello di applicare al calcolo delle somme le conoscenze acquisite . Tutto questo ci introdurrà al calcolo degli inetgrali, somme di infiniti infinitesimi.
Le differenze e le successioni¶
La figura seguente illustra, in un caso semplice, il problema centrale
di questo capitolo: quali valori ha la successione 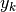 ?
Possiamo ricavarli a partire dai valori delle sue differenze? E se
riusciamo a ricostruire i risultati, saranno gli unici
possibili?
?
Possiamo ricavarli a partire dai valori delle sue differenze? E se
riusciamo a ricostruire i risultati, saranno gli unici
possibili?
Siccome la differenza 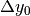 fra il primo e il secondo termine
è
fra il primo e il secondo termine
è 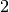 , avremo il secondo più grande di due unità rispetto al primo, cioè
, avremo il secondo più grande di due unità rispetto al primo, cioè
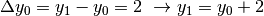 . Quindi se il primo termine è,
per esempio 10, allora il secondo è 12. Proseguendo così, il terzo risulta 15,
il quarto 16 e così via.
Purtroppo però nessuno garantisce che il primo sia
. Quindi se il primo termine è,
per esempio 10, allora il secondo è 12. Proseguendo così, il terzo risulta 15,
il quarto 16 e così via.
Purtroppo però nessuno garantisce che il primo sia 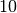 e i nostri
risultati valgono solo sotto questa ipotesi. Se il primo termine fosse invece
e i nostri
risultati valgono solo sotto questa ipotesi. Se il primo termine fosse invece
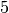 , la sequenza dei termini sarebbe:
, la sequenza dei termini sarebbe: 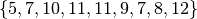 .
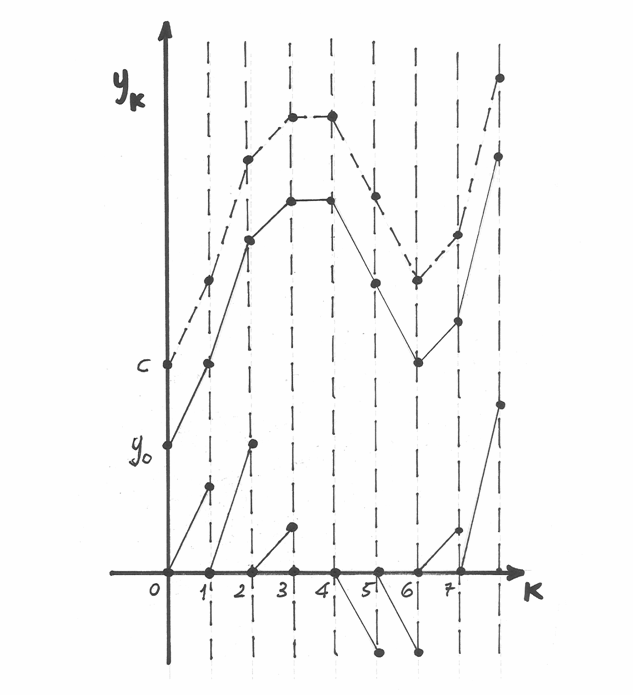
La sequenza delle differenze ci dà un’informazione incompleta, fornisce solo le
variazioni fra gli elementi delle successione. Nella figura seguente le variazioni
sono rappresentate dalle pendenze dei segmenti in basso, che partono tutti da zero.
.
La sequenza delle differenze ci dà un’informazione incompleta, fornisce solo le
variazioni fra gli elementi delle successione. Nella figura seguente le variazioni
sono rappresentate dalle pendenze dei segmenti in basso, che partono tutti da zero.
Solo se si conosce un valore qualsiasi della successione, il valore iniziale o
quello finale oppure uno dei valori intermedi, allora i singoli segmenti
formeranno un’unica spezzata. Non conoscendo il valore iniziale, lo chiamiamo
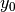 , oppure
, oppure  . Variando c, le spezzate sono infinite: tutte uguali
come andamento, ma distinte per il valore iniziale.
. Variando c, le spezzate sono infinite: tutte uguali
come andamento, ma distinte per il valore iniziale.
Pur tenendo conto di questa incertezza, possiamo riconoscere un’altra regola.
Partendo come prima da 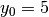 , il secondo termine si ottiene aggiungendo
la prima differenza, cioè
, il secondo termine si ottiene aggiungendo
la prima differenza, cioè 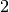 e il terzo aggiungendo la differenza successiva:
e il terzo aggiungendo la differenza successiva:
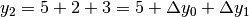 .
Con questa regola è facile ottenere l’ultimo termine: basta aggiungere al primo
termine la somma di tutte le differenze intermedie:
.
Con questa regola è facile ottenere l’ultimo termine: basta aggiungere al primo
termine la somma di tutte le differenze intermedie:
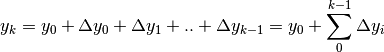
La lettera 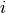 in quella posizione rappresenta l’indice di
in quella posizione rappresenta l’indice di 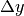 ,
che varia da
,
che varia da 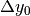 a
a 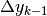
Anche le differenze di una successione formano una successione: la successione
delle differenze. Se diamo a questa successione il nome 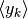 ,
l’esempio che abbiamo esaminato è un tentativo di ricostruire i valori
di una successione originaria
,
l’esempio che abbiamo esaminato è un tentativo di ricostruire i valori
di una successione originaria 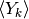 , conoscendo i suoi tassi
di variazione
, conoscendo i suoi tassi
di variazione 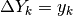 .
.
Esistenza della primitiva¶
Esiste sempre 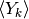 ? Sarà sempre possibile pensare una
successione come fosse la successione delle differenze di un’altra successione,
cioè sarà sempre possibile, partendo da una
? Sarà sempre possibile pensare una
successione come fosse la successione delle differenze di un’altra successione,
cioè sarà sempre possibile, partendo da una 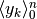 , trovare
una
, trovare
una 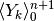 tale che sia
tale che sia 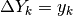 , e che
questo avvenga per tutti gli indici?
, e che
questo avvenga per tutti gli indici?
In realtà questo è sempre possibile, e le soluzioni sono infinite.
Infatti fissiamo dapprima un valore arbitrario 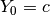 . Dato che la prima
differenza
. Dato che la prima
differenza 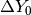 deve essere
deve essere 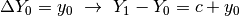 .
Quindi
.
Quindi 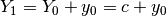 . Poi si prosegue con lo stesso ragionamento:
. Poi si prosegue con lo stesso ragionamento:
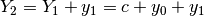 . Dopo qualche prova, perveniamo a:
. Dopo qualche prova, perveniamo a:
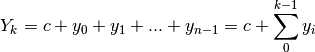
Poiché in generale le successioni partono da un indice 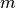 , possiamo riscrivere:
, possiamo riscrivere:
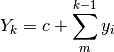
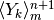 si dice primitiva della successione
si dice primitiva della successione
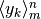 , se avviene che per
, se avviene che per 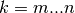 ,
,
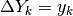 . Il variare di
. Il variare di  dà luogo a infinite
primitive.
dà luogo a infinite
primitive.
Note
Il termine primitiva troverà più avanti un’adeguata giustificazione, nel confronto con il termine derivata.
Un esempio¶
Applichiamo la regola precedente al caso più semplice: cerchiamo le primitive
della successione 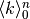 dei naturali.
La formula precedente diventa
dei naturali.
La formula precedente diventa
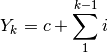
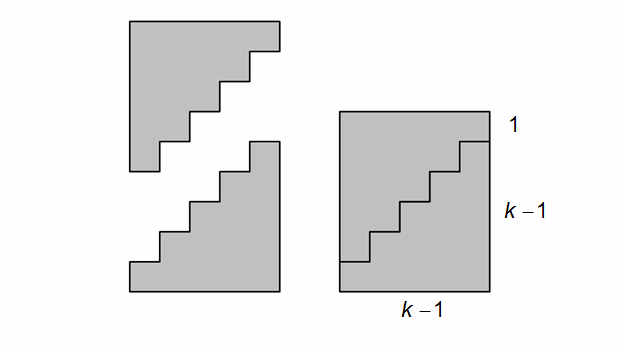
La somma in questione è quella di 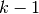 numeri naturali e vale
numeri naturali e vale
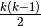 . Lo si può facilmente vedere pensando che
. Lo si può facilmente vedere pensando che 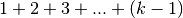 sia una somma di quadretti posti in strisce sovrapposte, in modo da formare una
gradinata. Nel disegno che segue la somma è per
sia una somma di quadretti posti in strisce sovrapposte, in modo da formare una
gradinata. Nel disegno che segue la somma è per 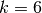 .
.
Quindi si ha: 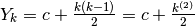 . Nel caso più
semplice (
. Nel caso più
semplice (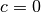 ) si ha la successione
) si ha la successione 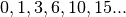 , le cui
differenze formano proprio la successione dei naturali. D’altronde le differenze
possono anche essere calcolate per via diretta con le regole che sappiamo:
, le cui
differenze formano proprio la successione dei naturali. D’altronde le differenze
possono anche essere calcolate per via diretta con le regole che sappiamo:
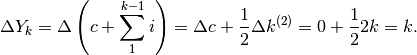
Le proprietà delle somme¶
Abiamo dunque trovato che è sempre possibile trovare le primitive di una successione e che queste si esprimono attraverso le somme. Quindi le proprietà delle somme diventano importanti per i nostri scopi e qui le riassumiamo brevemente.
Indichiamo con 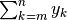 , oppure con
, oppure con 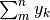 la
somma dei termini della successione
la
somma dei termini della successione 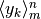 . L’espressione
di somma viene letta così: “somma per k che va da m a n”.
. L’espressione
di somma viene letta così: “somma per k che va da m a n”.  è una
variabile fittizia, cioè un indice che dice quale degli
è una
variabile fittizia, cioè un indice che dice quale degli 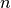 termini stiamo
sommando. Le proprietà della somma sono quelle usuali di linearità, cioè:
termini stiamo
sommando. Le proprietà della somma sono quelle usuali di linearità, cioè:
1) 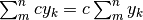 . (Dalla proprietà distributiva del prodotto
sulla somma).
. (Dalla proprietà distributiva del prodotto
sulla somma).
2) 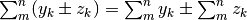 . (Dalla proprietà
commutativa della somma).
. (Dalla proprietà
commutativa della somma).
Inoltre si ha: 3) 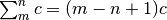 . (Somma di k termini tutti uguali)
. (Somma di k termini tutti uguali)
Le somme sono difficili da calcolare¶
Se la successione viene data in forma numerica, trovare le sue primitive è un calcolo semplice, che può essere affidato a un computer, se risulta laborioso. Invece sorgono problemi notevoli quando la successione è espressa attraverso una formula e quindi la primitiva deve essere una formula. Ovviamente la difficoltà sta nell’esprimere le somme, come si vede dai prossimi esempi.
Successione di potenze¶
Data 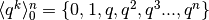 , applicando
la formula delle primitive, abbiamo:
, applicando
la formula delle primitive, abbiamo:
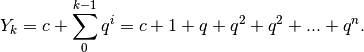
Per trovare il valore della somma che abbiamo sviluppato non c’è una regola
generale: dobbiamo ricorrere a qualche manipolazione algebrica. Chiamiamo  la somma degli
la somma degli  termini. Allora
termini. Allora
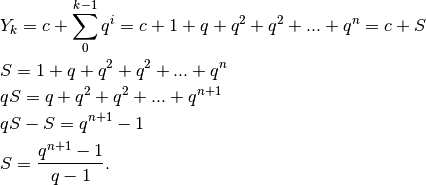
Se poniamo 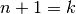 , abbiamo
, abbiamo 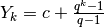 . Se la
frazione viene spezzata nella differenza di due frazioni, la seconda frazione non
contiene
. Se la
frazione viene spezzata nella differenza di due frazioni, la seconda frazione non
contiene  e quindi rappresenta una costante. Il risultato finale sarà:
e quindi rappresenta una costante. Il risultato finale sarà:
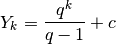
dove  questa volta è la costante che ingloba anche il secondo termine
della differenza.
questa volta è la costante che ingloba anche il secondo termine
della differenza.
Successione di quadrati¶
La successione dei quadrati 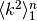 ha le primitive
date dalla formula
ha le primitive
date dalla formula
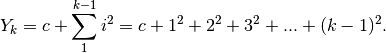
nel volume Iperreali, Cap.3.2, appiamo già ricavato per via grafica la formula della
somma di 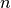 numeri quadrati:
numeri quadrati:
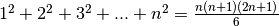 . Quindi, sostituendo
. Quindi, sostituendo 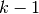 al posto di
al posto di 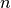 , abbiamo:
, abbiamo:
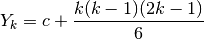
Conoscere già il risultato è un grande aiuto, infatti se dovessimo ricavarlo avremmo parecchi problemi.
Passiamo al controllo del risultato, calcolando le differenze.
Poiché 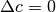 , Il calcolo è
, Il calcolo è
![\Delta Y_k&=\Delta\left[\frac{k(k-1)(2k-1)}{6}\right]=\frac{k(k+1)(2k+1}{6}-\frac{k(k-1)(2k-1)}{6}=\\ &=\frac{k}{6}\left[(2k^2+3k-1)-(2k^2-3k+1)\right]=\frac{k}{6}6k=k^2.](../../../_images/math/24fc4245cefcab07e4142cee8575f79a304c8fde.png)
Successione di prodotti fra coppie di successivi¶
Usando tecniche simili a quelle ricordate nel caso precedente, si ricava che
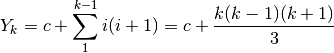
è la somma della successione
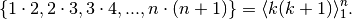
Ma anche senza ricorrere a tecniche grafiche, la cosa può essere dimostrata moltiplicando l’espressione sotto il segno di somma e ricorrendo alle proprietà già viste.
Verifichiamo invece le differenze:
![\Delta Y_k&=\Delta\left[\frac{k(k-1)(k+1)}{3}\right]=\frac{k(k+1)(k+2)}{3}-\frac{k(k-1)(k+1)}{3}=\\
&=\frac{k(k+1)}{3}[(k+2)-(k-1)]=\frac{k(k+1)}{3}3=k(k+1).](../../../_images/math/4a86d8b39848f76b432c00f487ac708134eeafab.png)
Successione di potenze moltiplicate per l’esponente¶
La successione
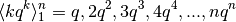
ha per primitiva
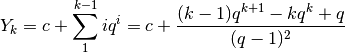
La dimostrazione della somma è piuttosto laboriosa, a meno di non ricorrere alle derivate. Infatti
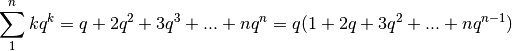
La somma tra parentesi è la derivata di 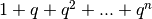 e, a sua volta,
questa somma è il risultato del quoziente
e, a sua volta,
questa somma è il risultato del quoziente 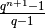 . Quindi:
. Quindi:
![D\left[\frac{q^{n+1}-1}{q-1}\right]&=\frac{(n+1)q^n(q-1)-(q^{n+1}-1)}{(q-1)^2}=\\
&=\frac{(n+1)q^{n+1}-(n+1)q^n-q^{n+1}+1}{(q-1)^2}=\\ &=\frac{nq^{n+1}-(n+1)q^n+1}{(q-1)^2}.](../../../_images/math/77f452dac90d611a499ac8497c63169ecee75a9f.png)
Moliplicando per 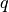 si ottiene la somma cercata:
si ottiene la somma cercata:
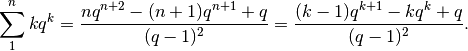
Note
Anche in questo caso si può spezzare la frazione precedente per isolare
l’addendo che non dipende da  , cioè
, cioè
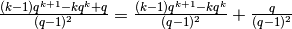 .
L’ultimo termine è quindi costante e può diventare parte della costante generica
.
L’ultimo termine è quindi costante e può diventare parte della costante generica  ,
per cui:
,
per cui: 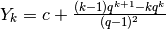 .
.
Conclusioni¶
Come si vede, non è per niente semplice calcolare le somme che entrano nell’espressione delle primitive. La difficoltà sta nel fatto che non si tratta solo di calcoli in genere piuttosto laboriosi, ma soprattutto della mancanza di una regola generale applicabile ad ogni caso.
Riassunto¶
- Il problema è come risalire ai termini di una successione conoscendo la successione delle sue differenze.
- In questa logica la successione prodotta dalle differenze è la successione
derivata, mentre la successione a cui risalire si chiama successione delle
primitive:
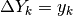 .
. - Le primitive di una successione sono infinite e differiscono l’una dall’altra per una costante.
- Se la successione delle differenze non è data per valori ma con una formula, per risalire alle primitive occorre calcolare le somme della successione.
- In generale il calcolo delle somme di una successione è difficile e manca una regola di riferimento.
Esercizi¶
- Dimostra le tre proprietà della somma esplicitando i simboli di sommatoria.
- I numeri dispari possono essere pensati come differenze fra due quadrati
successivi. Applica la definizione di primitiva alla successione dei dispari
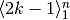 e usa le proprietà della somma per ricavare
le primitive
e usa le proprietà della somma per ricavare
le primitive 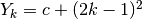 .
. - Spiega: se una successione ha i termini positivi, cosa si può dire delle sue differenze?
- Verifica il risultato precedente, calcolando le differenze delle somme ottenute.
- Scrivi e verifica un algoritmo che calcola i termini di una primitiva, man mano che legge i termini numerici di una successione.
- Completando l’ultimo passaggio nel par.2.6.1, verifica che la successione di potenze ha davvero la primitiva indicata e poi calcola le sue differenze.
- Seguendo le indicazioni date, dimostra la formula della primitiva della successione dei prodotti fra due naturali consecutivi, nel Par.2.6.3.
- Verifica che la primitiva del Par.2.6.4 ha per differenza la successione data.