I solidi di rotazione¶
L’integrale e il volume¶
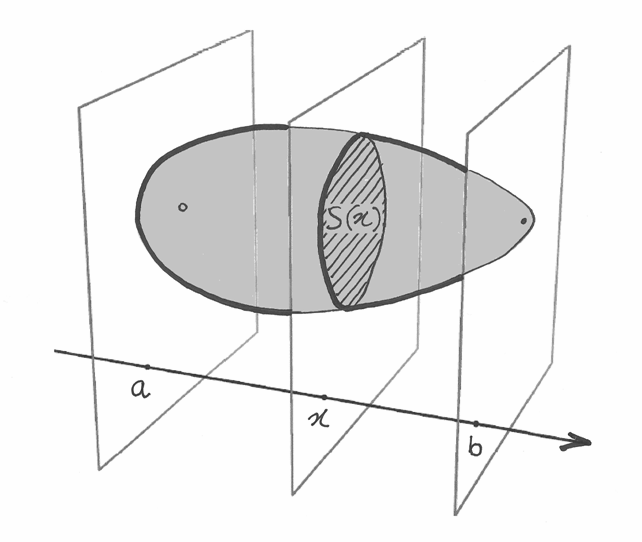
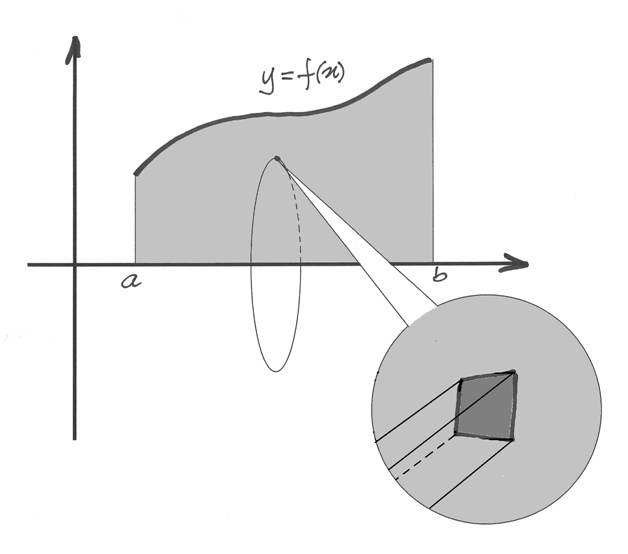
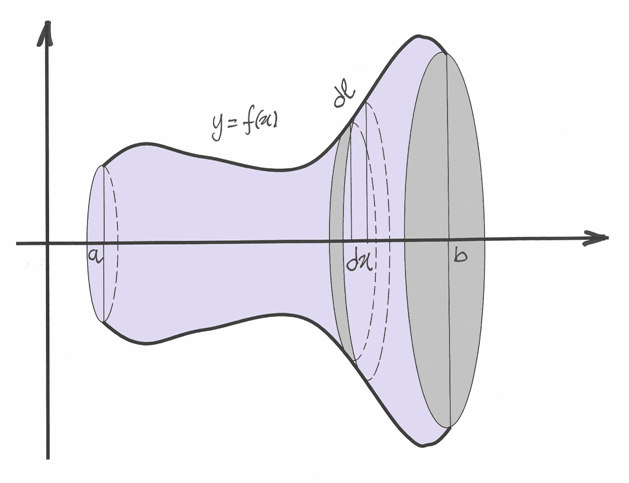
Immaginiamo un solido qualsiasi, compreso fra due piani paralleli 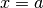 e
e
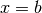 , del quale conosciamo l’area della sezione
perpendicolare
, del quale conosciamo l’area della sezione
perpendicolare 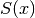 , per ogni punto
, per ogni punto 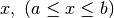 .
.
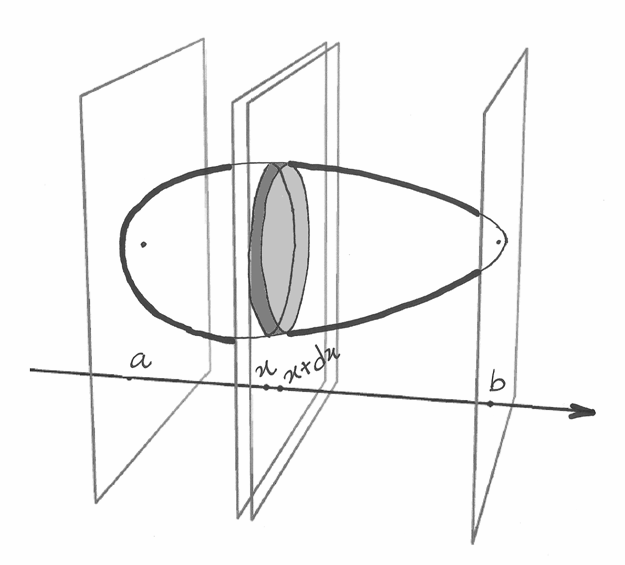
Conoscendo la sezione, il ragionamento non è difficile: basta immaginare di
tagliare il solido con due piani paralleli a distanza infinitesima 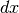 ,
così da individuare due superfici, di area
,
così da individuare due superfici, di area 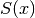 e
e 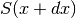 ,
infinitamente vicine e per questo indistinguibili, che formano le basi di
un cilindro di altezza
,
infinitamente vicine e per questo indistinguibili, che formano le basi di
un cilindro di altezza 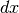 . La formula che si ottiene è in generale:
. La formula che si ottiene è in generale:
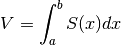
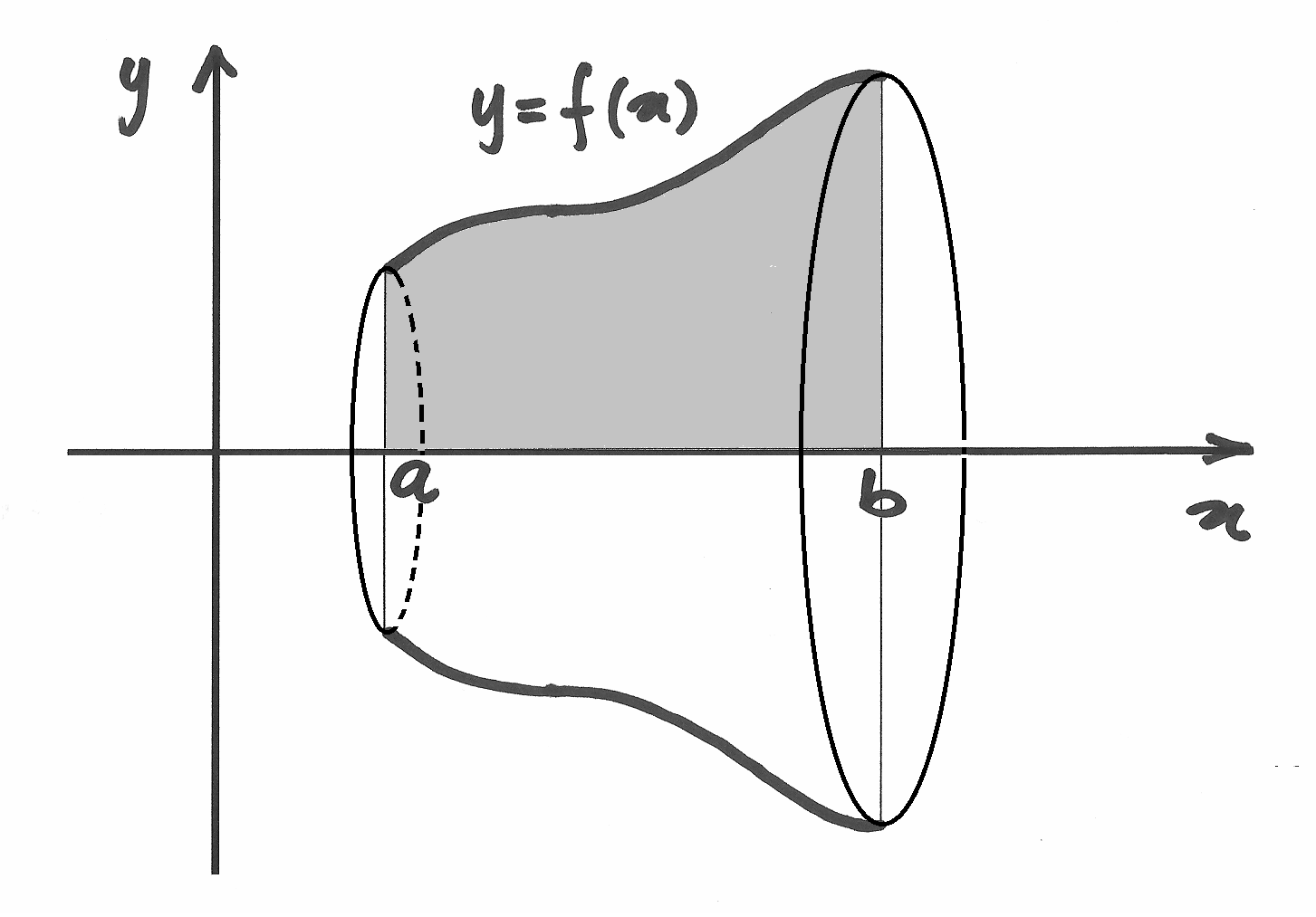
Vi sono solidi, ed è di questi che principalmente ci occupiamo, che possono
essere generati dalla rotazione di una superficie attorno ad un asse qualsiasi.
Per esempio si può ruotare il trapezoide di una funzione positiva attorno
all’asse delle ascisse. In questo caso la sezione in  individua un
cerchio di raggio
individua un
cerchio di raggio  e quindi la sua area è
e quindi la sua area è 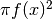 .
.
In questo caso la formula del volume diventa:
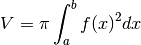
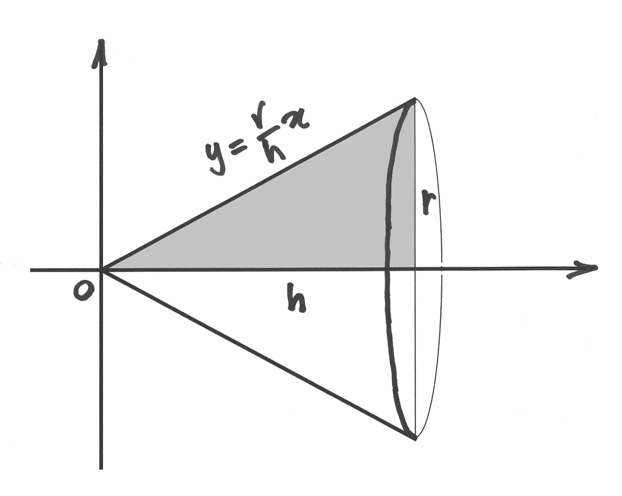
Per esempio, la formula usuale del volume di un cono si può ricavare pensando
al solido generato dalla rotazione di un triangolo rettangolo attorno alla sua
altezza 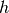 , coincidente con l’asse
, coincidente con l’asse  , in modo che il cateto
di base spazzi un cerchio di raggio
, in modo che il cateto
di base spazzi un cerchio di raggio  .
.
Allora l’ipotenusa coincide con la retta 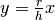 nell’intervallo
nell’intervallo
![[0,h]](../../../_images/math/9406d0e4d6fd729eb043402c15035503bf212081.png) . Il volume vale:
. Il volume vale:
![V=\pi\int_0^h\left(\frac{r}{h}x \right)^2 dx=\pi\int_0^h\frac{r^2}{h^2}x^2dx=
\frac{\pi r^2}{h^2}\left[\frac{x^3}{3} \right]_0^h=
\frac{\pi r^2}{h^2}\frac{x^3}{3}=\frac{1}{3}\pi r^2 h.](../../../_images/math/dfe94302e5a5345b79e17433d0dbc788469f5ab4.png)
I volumi simmetrici¶
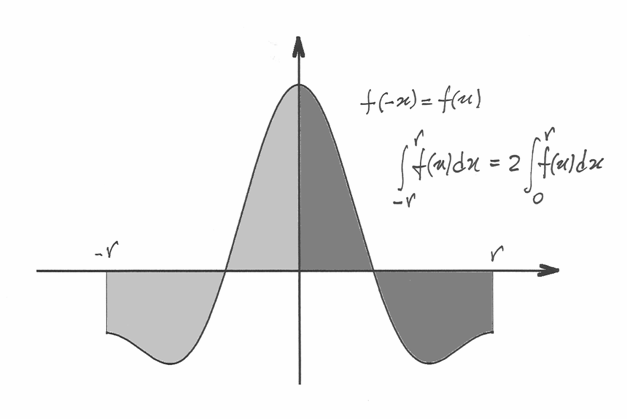
A volte i calcoli risultano più semplici prendendo in esame la simmetria della funzione che genera il trapezoide. Per esempio se una funzione è pari, allora
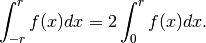
È questo il caso dell’Esercizio 1, per esempio.
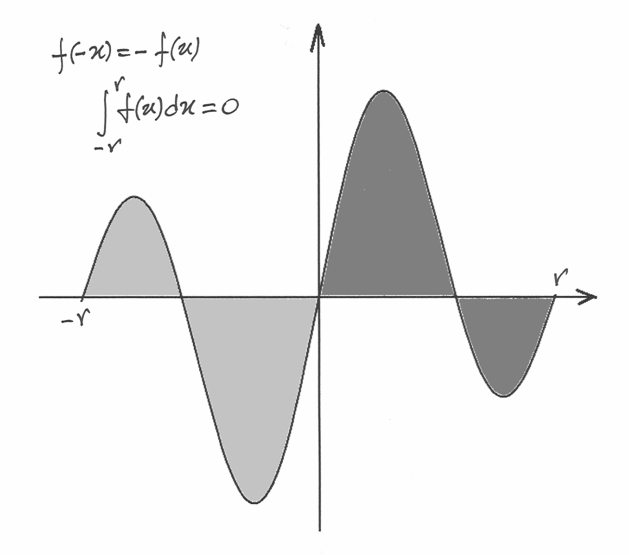
Invece, se la funzione è dispari, il volume generato dal suo trapezoidesu un intervallo simmetrico è nullo.
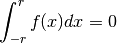
Questi due risultati intuitivi si possono dimostrare, spezzando l’integrale in due:
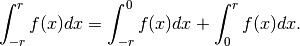
e sostituendo  con
con 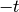 nel secondo integrale.
nel secondo integrale.
Se la funzione è pari, abbiamo:
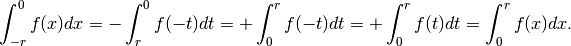
perché nelle funzioni pari 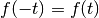 . Quindi:
. Quindi:
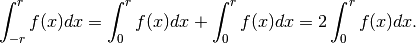
Invece, nelle funzioni dispari 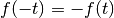 , per cui:
, per cui:
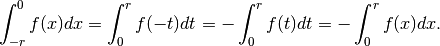
e quindi:
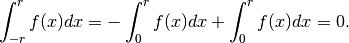
Il primo teorema di Guldin¶
C’è una proprietà notevole che lega il baricentro di un trapezoide al volume che esso genera ruotando intorno all’asse delle ascisse.
Se si prende una porzione infinitesima del trapezoide, di area 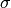 ,
collocata ad altezza
,
collocata ad altezza 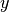 rispetto all’asse orizzontale, e la si fa ruotare
attorno a questo, si genera un anello il cui volume è indistinguibile da
rispetto all’asse orizzontale, e la si fa ruotare
attorno a questo, si genera un anello il cui volume è indistinguibile da
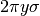 . Infatti
. Infatti 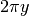 è la lunghezza (rettificata) del
suo percorso nella rotazione. L’ordinata y determina il valore del risultato,
sicchè porzioni di superficie vicine all’asse
è la lunghezza (rettificata) del
suo percorso nella rotazione. L’ordinata y determina il valore del risultato,
sicchè porzioni di superficie vicine all’asse  e porzioni lontane generano
anelli molto diversi. Per avere il calcolo esatto del volume generato dalla rotazione
di tutta la superficie occorrerebbe tener conto di tutti i diversi anelli.
Il teorema di Guldin afferma che è sufficiente tener conto della rotazione del
baricentro del trapezoide:
e porzioni lontane generano
anelli molto diversi. Per avere il calcolo esatto del volume generato dalla rotazione
di tutta la superficie occorrerebbe tener conto di tutti i diversi anelli.
Il teorema di Guldin afferma che è sufficiente tener conto della rotazione del
baricentro del trapezoide:
Il volume del solido di rotazione si ottiene moltiplicando l’area del trapezoide per il percorso del suo baricentro.
In formula, considerando  una funzione continua e positiva, definita
sull’intervallo
una funzione continua e positiva, definita
sull’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) :
:
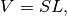
dove 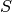 è la superficie del trapezoide:
è la superficie del trapezoide:
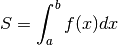
e L è la circonferenza tracciata dal baricentro nella rotazione:
Al numeratore si esprime il volume  del solido, mentre al denominatore si
esprime l’area
del solido, mentre al denominatore si
esprime l’area  del trapezoide.
del trapezoide.
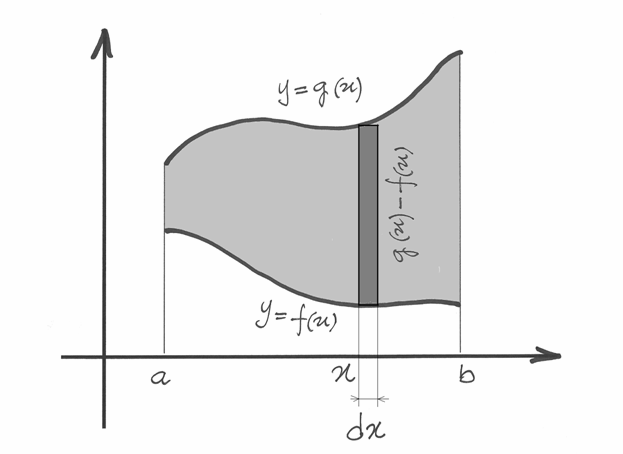
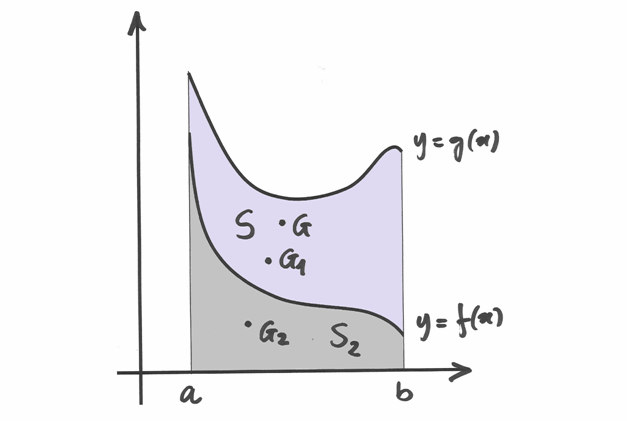
Il teorema di Guldin può essere usato anche in relazione a solidi generati dalla
rotazione di superfici diverse dai trapezoidi. Prendiamo ad esempio la regione di
piano compresa fra i grafici di due funzioni  e
e  , entrambe
definite su un intervallo
, entrambe
definite su un intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , in cui, per ogni
, in cui, per ogni  ,
, 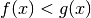 .
.
Il volume del solido di rotazione, in questo caso, è la differenza dei volumi generati dalla rotazione dei due trapezoidi, cioè:
![V=\pi\int_a^bg(x)^2dx-\pi\int_a^bf(x)^2dx=\pi\int_a^b\left[g(x)^2-f(x)^2\right]dx.](../../../_images/math/ca1372c07571ab06a3e289ef85524c82975bc2d4.png)
Si usa lo stesso metodo per l’area 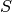 della superficie: possiamo pensarla
come integrale delle strisce indistinguibili dai rettangoli di larghezza
infinitesima
della superficie: possiamo pensarla
come integrale delle strisce indistinguibili dai rettangoli di larghezza
infinitesima 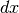 e di altezza
e di altezza 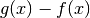 :
:
![S=\int_a^b[g(x)-f(x)]dx](../../../_images/math/e7f5e79e33d08c835939c6ff5f3a61d971c377a7.png)
Il baricentro di ogni striscia si trova nel punto medio, di ordinata: 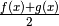 e la massa della striscia è
e la massa della striscia è ![dm=\sigma[g(x)-f(x)]](../../../_images/math/9c728d373d27a5d4ed1cb3759c27e3362f632efb.png) , con
, con 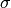 densità
superficiale. L’ordinata del baricentro è allora la media pesata delle ordinate
dei baricentri delle strisce:
densità
superficiale. L’ordinata del baricentro è allora la media pesata delle ordinate
dei baricentri delle strisce:
![y_G=\frac{\int_a^b\frac{f(x)+g(x)}{2}\sigma[g(x)-f(x)]dx}{\int_a^b\sigma[g(x)-f(x)]dx}=
\frac{\frac{\sigma}{2}\int_a^b[g(x)^2-f(x)^2]dx}{\sigma\int_a^b[g(x)-f(x)]dx}=
\frac{\int_a^b[g(x)^2-f(x)^2]dx}{2\int_a^b[g(x)-f(x)]dx}.](../../../_images/math/e00ce2c13b51c5e77a468c3019993aebbe2f1343.png)
Il percorso che il baricentro compie nella rotazione, allora sarà:
![L=2\pi y_G=\frac{\pi\int_a^b[g(x)^2-f(x)^2]dx}{\int_a^b[g(x)-f(x)]dx}=\frac{V}{S}.](../../../_images/math/71da9cb1655d80c27ed7163f67ead8fc008b12c2.png)
Applicazioni¶
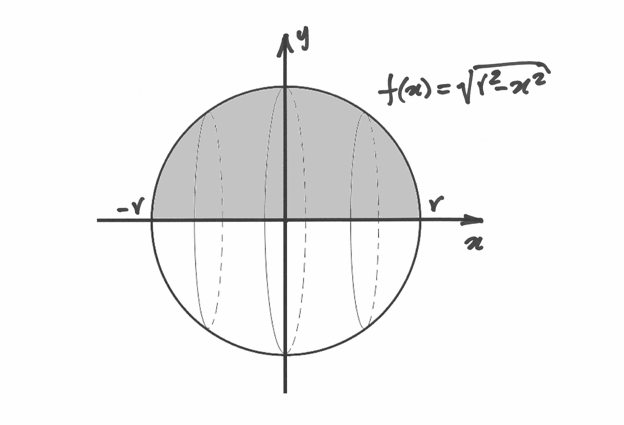
Il baricentro di un semicerchio¶
Sfruttiamo il teorema di Guldin per cercare il risultato già trovato nel capitolo
precedente. Pensiamo alla sfera generata dalla rotazione di un semicerchio. Il
suo volume è 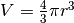 . La superficie che ruota ha area
. La superficie che ruota ha area
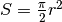 , quindi il percorso del baricentro è
, quindi il percorso del baricentro è
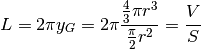
e la posizione del baricentro, considerando che 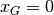 per questioni di
simmetria evidenti, si ricava da:
per questioni di
simmetria evidenti, si ricava da:
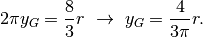
Esercizio sul primo teorema di Guldin¶
Dimostrare il teorema relativamente alla regione compresa fra i grafici di due funzioni, senza calcolare il baricentro.
Dal disegno vediamo che la regione che ci interessa è 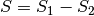 , che
genera, ruotando, un volume
, che
genera, ruotando, un volume 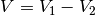 . Il trapezoide
di
. Il trapezoide
di 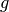 ha baricentro
ha baricentro 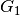 , quello di
, quello di  ha baricentro
ha baricentro
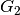 e
e 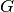 è il baricentro della regione che ci interessa.
Consideriamo che la regione sia omogenea, cioè con densità costante, e sfruttiamo
la proprietà additiva del baricentro, come se la massa di ogni regione fosse
concentrata nel suo baricentro. Facendo ricorso alla media pesata, abbiamo:
è il baricentro della regione che ci interessa.
Consideriamo che la regione sia omogenea, cioè con densità costante, e sfruttiamo
la proprietà additiva del baricentro, come se la massa di ogni regione fosse
concentrata nel suo baricentro. Facendo ricorso alla media pesata, abbiamo:
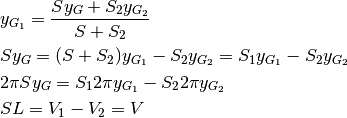
L’ultimo passaggio si ottiene applicando il teorema ai trapezoidi.
Il secondo teorema di Guldin¶
Il secondo teorema riguarda la superficie di rotazione, ottenuta dal
movimento di una curva piana, che immaginiamo essere il grafico di una
funzione, attorno all’asse  .
.
La superficie viene pensata come composta da infiniti anelli
di spessore infinitesimo, ciascuno ottenuto sezionando la superficie con due
piani paralleli distanti 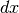 l’uno dall’altro. L’area di un anello
è indistinguibile dall’area di un rettangolo. La base del rettangolo è la
circonferenza, cioè
l’uno dall’altro. L’area di un anello
è indistinguibile dall’area di un rettangolo. La base del rettangolo è la
circonferenza, cioè 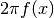 , e la sua altezza è il tratto infinitesimo
, e la sua altezza è il tratto infinitesimo
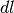 del grafico, che vale
del grafico, che vale 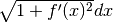 , se la funzione è
derivabile (vedi capitolo precedente). L’area della superficie è allora
l’integrale di questi rettangoli:
, se la funzione è
derivabile (vedi capitolo precedente). L’area della superficie è allora
l’integrale di questi rettangoli:
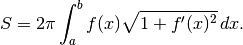
Proviamo ora a ragionare sul grafico e sul suo baricentro, riferendoci a quanto visto nell’ultimo paragrafo del Cap.8. La lunghezza del grafico è:
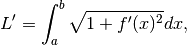
mentre l’ordinata del baricentro del grafico è:
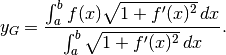
Poichè un anello descritto dalla rotazione del baricentro ha lunghezza
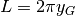 , vale
, vale 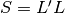 , cioè:
, cioè:
l’area della superficie, ottenuta ruotando una curva piana, si ottiene moltiplicando la lunghezza della curva per la lunghezza del percorso che il baricentro della curva traccia durante la rotazione.
Analogamente al caso dei volumi, possiamo usare il teorema per calcolare l’area di una superficie oppure, avendo già questo risultato per altra via, per calcolare la posizione del baricentro della curva.
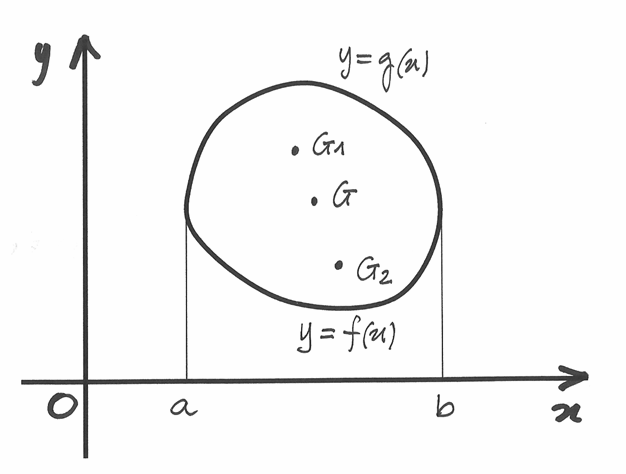
Generalizzazione dei due teoremi¶
I teroremi di Guldin valgono anche se la curva piana è chiusa, perché si può pensarla come l’unione dei grafici di due funzioni definite sullo stesso intervallo.
Riferendoci al disegno, abbiamo due baricentri: 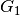 per la curva superiore,
grafico di
per la curva superiore,
grafico di 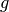 , e
, e 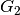 per la curva inferiore, grafico di
per la curva inferiore, grafico di  .
Se la lunghezza complessiva è
.
Se la lunghezza complessiva è 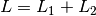 , abbiamo che il baricentro
dell’intera curva è
, abbiamo che il baricentro
dell’intera curva è
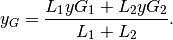
Da qui si ricava che 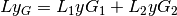 e , moltiplicando per il
percorso tracciato durante la rotazione, si ottiene:
e , moltiplicando per il
percorso tracciato durante la rotazione, si ottiene:
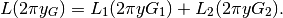
In pratica significa che l’area della superficie complessiva è data della somma
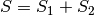 . Sembra un risultato elementare, se non si considera che le aree
sono calcolate ruotando i baricentri.
. Sembra un risultato elementare, se non si considera che le aree
sono calcolate ruotando i baricentri.
In realtà non è necessario che il baricentro compia una rotazione completa e nemmeno che si muova lungo un arco di circonferenza. Anche se Guldin non l’aveva previsto, i suoi teoremi valgono per qualsiasi movimento che il trapezoide, la regione piana, il grafico o la curva compiono perpendicolarmente al piano su cui si trovano.
Esercizio¶
Calcola la superficie generata dalla rotazione di 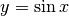 , definita
in
, definita
in ![[0,\pi]](../../../_images/math/1b989a72aeaf778381894e0025fe309783e17235.png) .
.
L’integrale che esprime la superficie è:
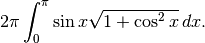
L’integrale, calcolato al computer con Derive, dà 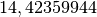 Risolvendo a mano, poniamo
Risolvendo a mano, poniamo 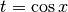 , per cui
, per cui
![&2\pi\int_0^\pi \sin x\sqrt{1+\cos^2 x}\, dx=
-2\pi\int_1^{-1}\sqrt{1+t^2}\, dt=2\pi\int_{-1}^1\sqrt{1+t^2}\, dt=\\
&=2\pi\cdot 2\int_0^1\sqrt{1+t^2}\, dt=
2\pi\left[t\sqrt{1+t^2}+\ln\left(\sqrt{1+t^2}+t \right) \right]_0^1 =
2\pi\left[\sqrt{2}+\ln(\sqrt{2}+1) \right].](../../../_images/math/5ebc11af6d4f120e5937590b00e97eb8aa3e1ecf.png)
Con una calcolatrice si può verificare che il risultato corrisponde.
Invece, per quanto riguarda la lunghezza dell’arco, che si ottiene integrando
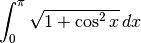
dobbiamo affrontare un integrale estremamente difficile. Il risultato, che si
ottiene con metodi approssimati, è 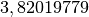 .
.
Riassunto¶
Il volume di un solido si può ottenere immaginando di dividerlo trasversalmente con piani paralleli distanti l’uno dall’altro un infinitesimo, rilevando l’area della sezione
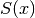 su ogni piano e integrando su tutto l’intervallo
definito dal primo e ultimo piano che limitano il solido:
su ogni piano e integrando su tutto l’intervallo
definito dal primo e ultimo piano che limitano il solido: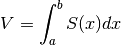
Se nel piano cartesiano abbiamo il grafico di una funzione positiva, definita su un intervallo, chiamiamo trapezoide la regione sottesa. Si ottiene un solido di rotazione ruotando il trapezoide attorno all’asse
 .
In questo caso il volume si calcola con:
.
In questo caso il volume si calcola con: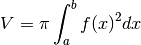
Il calcolo può essere facilitato, tenendo conto di eventuali simmetrie della funzione.
I teoremi di Guldin semplificano i calcoli del volume e della superficie dei solidi di rotazione, basandosi sul percorso che fa il baricentro durante la rotazione.
Per il volume, il primo teorema di Guldin dice che è:
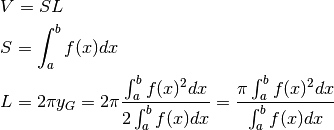
con
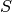 area della superficie del trapezoide e
area della superficie del trapezoide e 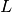 lunghezza della
circonferenza disegnata dal baricentro
lunghezza della
circonferenza disegnata dal baricentro 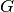 .
.Per la superficie, il secondo teorema di Guldin dice che:
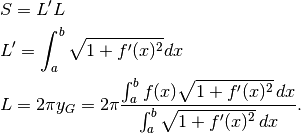
con
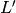 lunghezza della curva che rappresenta il grafico di
lunghezza della curva che rappresenta il grafico di  su
su ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) e
e 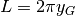 circonferenza tracciata dal baricentro
della curva.
circonferenza tracciata dal baricentro
della curva.I teoremi di Guldin si applicano anche a regioni del piano racchiuse fra due grafici e ai loro perimetri.
Se il volume del solido, o la sua superficie, sono conosciuti per altra via, i teoremi di Guldin semplificano la ricerca del baricentro.
Esercizi¶
Ricava la formula del volume di una sfera, immaginando la rotazione del trapezoide in grigio nel disegno.
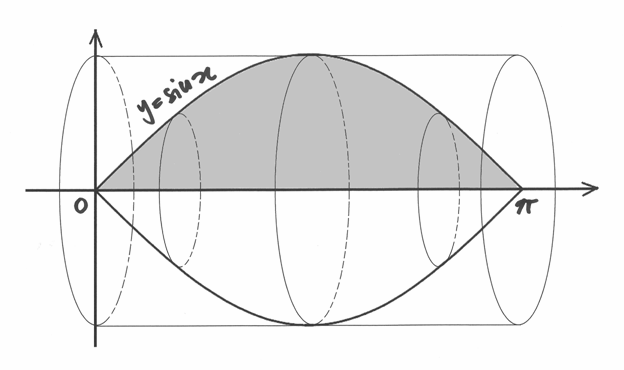
Ricava il volume del solido generato dalla rotazione del trapezoide di
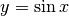 nell’intervallo
nell’intervallo ![[0, \pi]](../../../_images/math/382cd28a1b99d9ce284e1888b78cd9554e6f335c.png) , e ricava
quale parte è il solido rispetto al cilindro tangente.
, e ricava
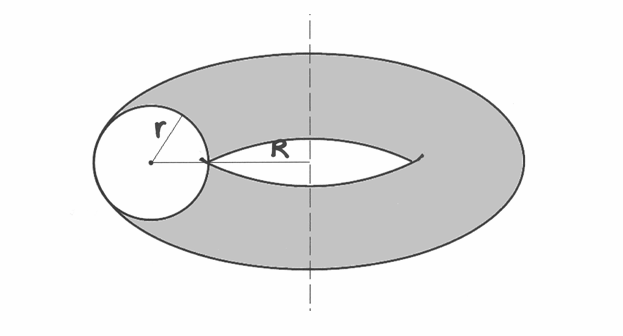
quale parte è il solido rispetto al cilindro tangente.Ricava il volume del toro rappresentato in figura.
Calcola il baricentro di una semicirconferenza, a partire dall’area della superficie sferica ottenuta dalla rotazione di questa, e confronta il risultato con quello del capitolo precedente.
Calcola l’area della superficie di un toro di raggi
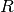 e
e  .
.