Massimi, minimi e flessi¶
Due problemi di ottimizzazione¶
I due problemi seguenti orienteranno il nostro studio a prendere confidenza con le applicazioni più tipiche. Il primo problema è già stato oggetto di studio nel libro sugli iperreali.
La scatola più capiente¶
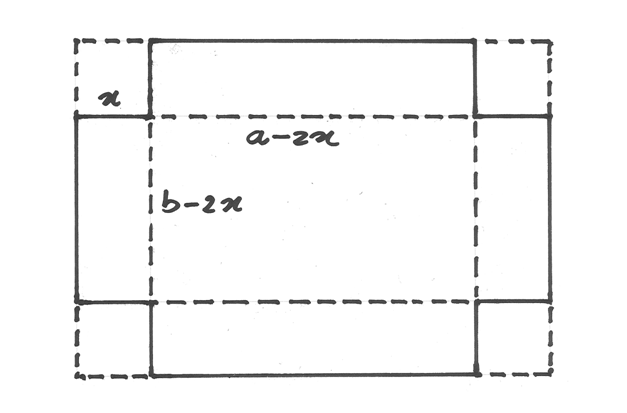
Partendo da un cartoncino di formato A4, si cerca di ricavare la scatola (senza coperchio) più capiente, praticando alla giusta distanza due tagli perpendicolari a lato di ogni angolo, in modo da escludere in tutto 4 quadrati uguali. Calcola al millimetro la misura dei tagli opportuna.
I fogli di formato A sono costruiti così: il foglio A0 è un rettangolo di area
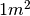 e con lati in rapporto uguale a
e con lati in rapporto uguale a 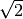 . Viene diviso a metà
lungo il suo lato maggiore per ottenere due fogli di formato A1,
i quali a loro volta vengono tagliati con lo stesso criterio, formando ciascuno
due fogli di formato A2. Lo stesso avviene per i formati successivi, che indicano
fogli sempre più piccoli, con l’area dimezzata rispetto ai formati precedenti.
Quindi se a è il lato maggiore per esempio del rettangolo di formato A3 e b
è il lato maggiore del rettangolo di formato A4, si ha che
. Viene diviso a metà
lungo il suo lato maggiore per ottenere due fogli di formato A1,
i quali a loro volta vengono tagliati con lo stesso criterio, formando ciascuno
due fogli di formato A2. Lo stesso avviene per i formati successivi, che indicano
fogli sempre più piccoli, con l’area dimezzata rispetto ai formati precedenti.
Quindi se a è il lato maggiore per esempio del rettangolo di formato A3 e b
è il lato maggiore del rettangolo di formato A4, si ha che
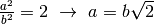 , che è anche il rapporto fra le
dimensioni di uno stesso foglio. Siccome il foglio formato A0 ha area di
, che è anche il rapporto fra le
dimensioni di uno stesso foglio. Siccome il foglio formato A0 ha area di
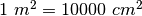 , il foglio di formato A4 avrà area
, il foglio di formato A4 avrà area
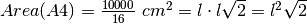 , dove
, dove
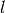 è il lato per esempio minore. Quindi
è il lato per esempio minore. Quindi
![a^2\sqrt{2}= \frac{10000}{16}\ \to \ a=\frac{25}{\sqrt[4]{2}}=21.02241\ cm](../../../_images/math/c86acfa07d193472bb779c7c7506b03438cec93d.png) .
Moltiplicando per
.
Moltiplicando per 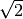 si ottiene l’altra dimensione, di
si ottiene l’altra dimensione, di 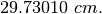
Per indicare più brevemente i calcoli poniamo 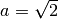 e
e 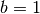 .
Una volta ottenuto il risultato lo moltiplicheremo per il vero valore di
.
Una volta ottenuto il risultato lo moltiplicheremo per il vero valore di
![b=\frac{25}{\sqrt[4]{2}}](../../../_images/math/495bd0531b3e7c3aab1558789c0a21d7fadd853a.png) .
Le dimensioni iniziali della scatola ideale vengono accorciate di
.
Le dimensioni iniziali della scatola ideale vengono accorciate di 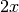 ,
così avremo un volume pari a
,
così avremo un volume pari a 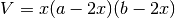 . Per cercare il volume massimo
consideriamo la funzione
. Per cercare il volume massimo
consideriamo la funzione 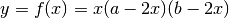 , definita nell’intervallo
, definita nell’intervallo
![\left[0,\frac{b}{2}\right]](../../../_images/math/473f86cf585ef530cd2893a4e3c6c4d77eb2d49f.png) , perché non si può pensare di praticare il taglio
oltre la metà del lato minore. Consideriamo gli estremi dell’intervallo inclusi:
sappiamo che a distanza zero e a distanza
, perché non si può pensare di praticare il taglio
oltre la metà del lato minore. Consideriamo gli estremi dell’intervallo inclusi:
sappiamo che a distanza zero e a distanza  da un vertice
non ha senso praticare il taglio perché il volume risulta nullo:
da un vertice
non ha senso praticare il taglio perché il volume risulta nullo:
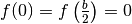 .
Senza nessun taglio, la scatola non esiste e il volume è nullo. Si provano
tagli via via più profondi e più distanti dai vertici, si piegano i margini,
la scatola prende forma e il volume cresce. Sia arriverà ad un taglio
(almeno uno) di misura
.
Senza nessun taglio, la scatola non esiste e il volume è nullo. Si provano
tagli via via più profondi e più distanti dai vertici, si piegano i margini,
la scatola prende forma e il volume cresce. Sia arriverà ad un taglio
(almeno uno) di misura 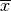 che darà luogo al volume massimo.
Il grafico di
che darà luogo al volume massimo.
Il grafico di  , in corrispondenza di
, in corrispondenza di 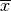 avrà
la tangente orizzontale, perché la funzione che rappresenta il volume cresce fino
al suo massimo, poi decresce. Quindi per
avrà
la tangente orizzontale, perché la funzione che rappresenta il volume cresce fino
al suo massimo, poi decresce. Quindi per 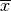 la derivata della
funzione si annulla.
la derivata della
funzione si annulla.
Calcoliamo la derivata e poniamola uguale a zero:
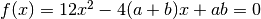 . È un’equazione di secondo grado, le cui
soluzioni sono accettabili solo se appartengono all’intervallo dato.
Le considerazioni precedenti ci dicono che almeno una soluzione deve esistere:
ne abbiamo la certezza esaminando
. È un’equazione di secondo grado, le cui
soluzioni sono accettabili solo se appartengono all’intervallo dato.
Le considerazioni precedenti ci dicono che almeno una soluzione deve esistere:
ne abbiamo la certezza esaminando
![\frac{\Delta}{4}=4(a+b)^2-12ab=4(a^2-ab+b^2)=4[(a-b)^2+ab]>0](../../../_images/math/3868f4a1066b941b534c5d372d380e4c30979b8d.png) .
Quindi
.
Quindi
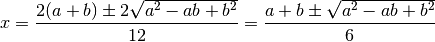
Sostituendo 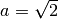 e
e 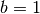 si ottiene una sola soluzione
nell’intervallo dato
si ottiene una sola soluzione
nell’intervallo dato 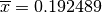 e infine, moltiplicando per
e infine, moltiplicando per
![\frac{25}{\sqrt[4]{2}}](../../../_images/math/dd374d63b8dfe0e597a9463cca72afd997c65975.png) si perviene al valore
si perviene al valore 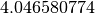 .
Il taglio ottimale risulta perciò di circa
.
Il taglio ottimale risulta perciò di circa 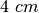 .
.
Il cilindro di area minima¶
Fra tutti i cilindri di volume dato, trova le dimensioni del cilindro con la minima area totale.
La formula che esprime il volume di un cilindro è 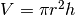 (r è
il raggio, h è l’altezza). Se il volume è dato, l’altezza dipende dal raggio:
(r è
il raggio, h è l’altezza). Se il volume è dato, l’altezza dipende dal raggio:
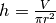 . La formula della superficie totale dipende anch’essa
da altezza e raggio:
. La formula della superficie totale dipende anch’essa
da altezza e raggio: 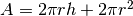 e può essere riscritta come
funzione che dipende unicamente dal raggio
e può essere riscritta come
funzione che dipende unicamente dal raggio 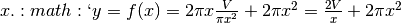 .
.
Il primo addendo indica l’area laterale. Poiché il raggio vi compare al denominatore,
vuol dire che l’area laterale è infinita se il raggio è infinitesimo,
cioè il cilindro è sottilissimo e altissimo. In questo caso le due aree di base,
cioè il secondo addendo, danno un contributo infinitesimo. Al contrario,
se il raggio è infinito, l’area laterale risulta infinitesima e le aree di base
sono infinite, cioè il cilindro è piatto e larghissimo. Fra queste due situazioni
estreme ci sarà senz’altro un valore intermedio del raggio tale da rendere
minima l’area totale. La funzione è definita nell’intervallo 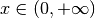
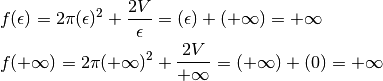
 ha quindi un grafico che scende dall’infinito per
ha quindi un grafico che scende dall’infinito per  prossimo
a
prossimo
a  e vi risale per
e vi risale per 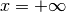 . Il grafico ha senz’altro almeno un
punto di minimo, nel quale la tangente è orizzontale, come già visto.
. Il grafico ha senz’altro almeno un
punto di minimo, nel quale la tangente è orizzontale, come già visto.
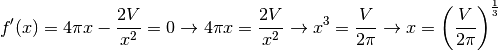
Il risultato non è tanto importante in sè, perché un semplice algoritmo, eseguito al computer, avrebbe potuto calcolarlo per ogni dato volume. E’ invece significativo perché ci dà indicazioni preziose sulla forma del solido. Mettiamo in rapporto l’altezza e il raggio:
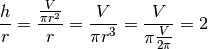
Fra gli infiniti cilindri di dato volume, quello di area minima ha l’altezza pari al diametro. La sua sezione verticale passante per il diametro è quindi un quadrato.
Note
Restando aderenti alle situazioni concrete, si danno per scontate alcune questioni teoriche (sulla continuità delle funzioni, sull’esistenza della soluzione, ecc), e i procedimenti risolutivi arrivano ai risultati senza intoppi. Non tutti i casi sono però così fortunati, quindi ora è il momento di esaminare la questione nei suoi aspetti generali.
Generalità sui massimi e sui minimi¶
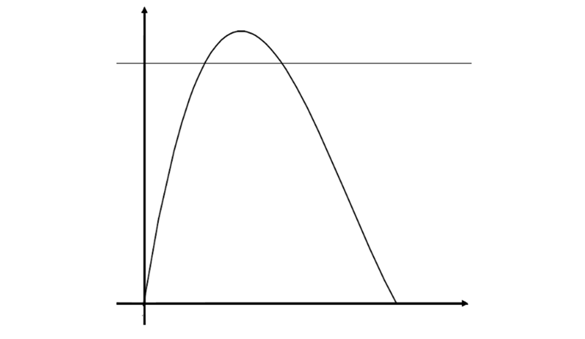
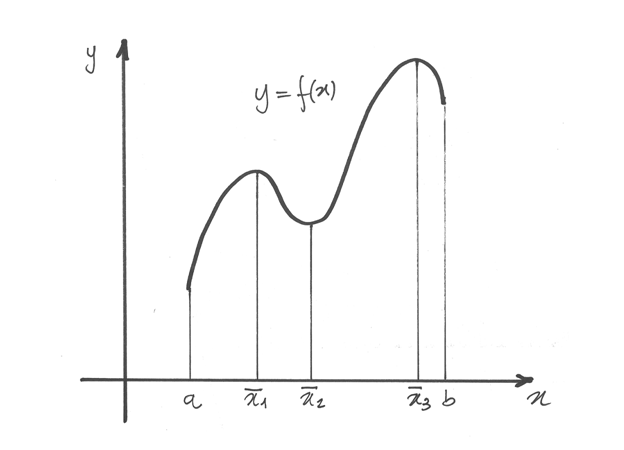
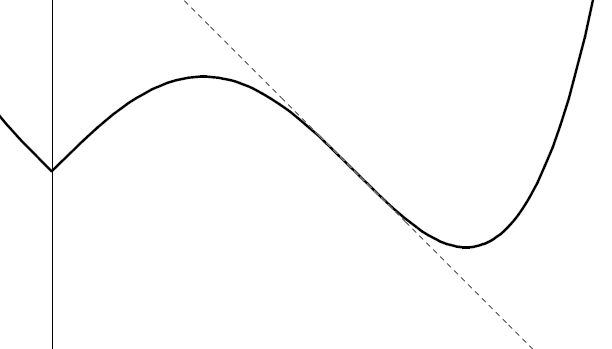
Il disegno mostra il grafico di una funzione che due punti di massimo relativo
in 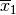 e
e 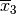 , di cui quest’ultimo è anche
massimo assoluto, e tre punti di minimo relativo in
, di cui quest’ultimo è anche
massimo assoluto, e tre punti di minimo relativo in 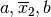 ,
fra i quali
,
fra i quali  è anche minimo assoluto.
è anche minimo assoluto.
- Massimo assoluto vuol dire
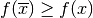 per tutti gli
per tutti gli
 del dominio.
del dominio. - Massimo relativo:
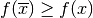 per tutti gli
per tutti gli
 del dominio, infinitamente vicini a
del dominio, infinitamente vicini a 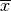 .
. - Minimo assoluto vuol dire
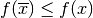 per tutti gli
per tutti gli
 del dominio.
del dominio. - Minimo relativo:
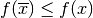 per tutti gli
per tutti gli
 del dominio, infinitamente vicini a
del dominio, infinitamente vicini a 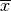 .
.
Non è detto che una funzione abbia un massimo assoluto: può averne uno, nessuno
o anche infiniti e lo stesso vale per i minimi assoluti. Una funzione come la
tangente, nell’intervallo 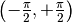 ,
oppure come la retta
,
oppure come la retta 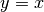 nell’intervallo
nell’intervallo 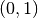 , non ha né massimi
né minimi. Invece la funzione seno, considerata sull’asse iperrereale, ha infiniti
massimi e minimi assoluti. La questione dell’esistenza certa di massimi o minimi
assoluti è legata alla continuità della funzione e al fatto che l’intervallo
contenga gli estremi. Questo non esclude che anche altre funzioni, discontinue oppure definite su intervalli aperti, abbiano di questi punti.
, non ha né massimi
né minimi. Invece la funzione seno, considerata sull’asse iperrereale, ha infiniti
massimi e minimi assoluti. La questione dell’esistenza certa di massimi o minimi
assoluti è legata alla continuità della funzione e al fatto che l’intervallo
contenga gli estremi. Questo non esclude che anche altre funzioni, discontinue oppure definite su intervalli aperti, abbiano di questi punti.
Teorema: Se una funzione  è continua e definita su un intervallo
chiuso e limitato
è continua e definita su un intervallo
chiuso e limitato ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , allora certamente esiste un punto
, allora certamente esiste un punto
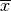 interno all’intervallo per il quale la funzione ha un massimo
(minimo) assoluto.
interno all’intervallo per il quale la funzione ha un massimo
(minimo) assoluto.
Dimostrazione: Consideriamo ![f:\ [a,b]\ \to \mathbf{R}](../../../_images/math/b694b6ea4844f89478c00b7560d42e5dc7d6d01f.png) .
Poniamo
.
Poniamo 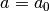 e
e 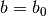 .
Dividiamo l’intervallo per il suo punto medio
.
Dividiamo l’intervallo per il suo punto medio 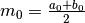 e
andiamo a cercare se in
e
andiamo a cercare se in ![[a_0,m_0]](../../../_images/math/a27ee0708e672a1ca5fb129017e6dabb3c02510a.png) esiste un punto
esiste un punto 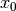 tale
che in quel punto la funzione supera (o eguaglia) i valori che assume
nella seconda metà
tale
che in quel punto la funzione supera (o eguaglia) i valori che assume
nella seconda metà ![[m_0,b]](../../../_images/math/8fbb6af77ebf426ba9b3f976392e68f48942e8ed.png) :
: ![f(x_0)\ge ~f(x), ~\forall x\in [m_0,b]](../../../_images/math/b2cd9d7ebe1a6a6e9a118a90953b57508de59540.png) .
Se questo
.
Se questo 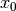 esiste, allora concentriamo il lavoro successivo solo
sulla prima metà di
esiste, allora concentriamo il lavoro successivo solo
sulla prima metà di ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , cioè su
, cioè su ![[a_0,m_0]](../../../_images/math/a27ee0708e672a1ca5fb129017e6dabb3c02510a.png) , altrimenti
ci concentreremo sulla seconda metà,
, altrimenti
ci concentreremo sulla seconda metà, ![[m_0,b]](../../../_images/math/8fbb6af77ebf426ba9b3f976392e68f48942e8ed.png) . Nel primo caso poniamo
. Nel primo caso poniamo
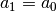 e
e 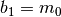 , nel secondo sarà:
, nel secondo sarà: 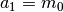 e
e 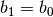 . A questo punto si ripete il procedimento: si trova il punto
medio del nuovo intervallo
. A questo punto si ripete il procedimento: si trova il punto
medio del nuovo intervallo 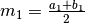 e ci si concentra
sulla metà che contiene
e ci si concentra
sulla metà che contiene 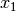 tale
tale 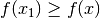 per tutti gli
per tutti gli
 dell’altra metà. E così via. Con questa tecnica si costruiscono due
successioni dei valori
dell’altra metà. E così via. Con questa tecnica si costruiscono due
successioni dei valori 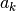 e
e 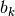 , che rappresentano gli estremi
sempre più vicini di intervalli che si stringono sempre più attorno al punto
per il quale
, che rappresentano gli estremi
sempre più vicini di intervalli che si stringono sempre più attorno al punto
per il quale  assume un valore maggiore o uguale a tutti quelli assunti per gli
assume un valore maggiore o uguale a tutti quelli assunti per gli  esterni.
Le due successioni sono monotone e limitate, quindi convergono (v. Par. 13.1.2).
La differenza fra due termini
esterni.
Le due successioni sono monotone e limitate, quindi convergono (v. Par. 13.1.2).
La differenza fra due termini 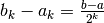 è infinitesima per indici infiniti:
è infinitesima per indici infiniti: 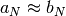 Le due successioni convergono allo stesso numero standard
Le due successioni convergono allo stesso numero standard 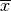 ,
con
,
con 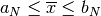 e
e 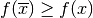 per
tutti gli
per
tutti gli  esterni alla monade di
esterni alla monade di 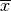 .
Quindi
.
Quindi  ha in
ha in 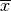 un punto di massimo assoluto.
un punto di massimo assoluto.
Note
Il teorema vale anche per i punti di minimo assoluto. Basta infatti
considerare la funzione 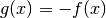 e procedere con una dimostrazione analoga.
e procedere con una dimostrazione analoga.
Teorema. Nei punti di massimo (minimo) interni a ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) la derivata si annulla.
la derivata si annulla.
Infatti se il punto  è di massimo,
è di massimo, 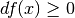 . Per
. Per 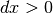 si ha
si ha 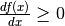 , mentre se
, mentre se 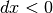
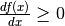 . La parte standard del rapporto differenziale
non può essere contemporaneamente positiva e negativa, perciò
. La parte standard del rapporto differenziale
non può essere contemporaneamente positiva e negativa, perciò 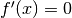 .
.
Note
Anche gli estremi dell’intervallo possono essere di massimo o di minimo,
ma non è detto che la derivata in quei punti sia nulla. Per esempio questo accade
per 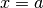 nel disegno. Inoltre vi possono essere massimi e minimi
per i quali la derivata non esiste, come per
nel disegno. Inoltre vi possono essere massimi e minimi
per i quali la derivata non esiste, come per 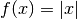 nell’origine.
nell’origine.
In conclusione una funzione definita e continua su un intervallo chiuso e limitato ha certamente un massimo e un minimo assoluti e questi punti vanno cercati dove la derivata si annulla, oppure agli estremi dell’intervallo oppure dove la derivata non esiste.
Esempio 1¶
Cercare massimi e minimi di 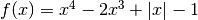
La funzione è continua, perché è somma di funzioni continue. All’infinito
è asintotica a 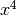 , quindi diverge positivamente:
, quindi diverge positivamente:
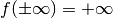 . La funzione ha quindi un minimo assoluto, non
un massimo assoluto, oltre ad altri eventuali massimi e minimi relativi.
. La funzione ha quindi un minimo assoluto, non
un massimo assoluto, oltre ad altri eventuali massimi e minimi relativi.
Ricerca del minimo assoluto¶
Il punto va ricercato
- dove eventualmente si annulla la derivata, oppure
- dove la derivata non esiste, cioè in
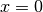 .
.
Per capire quest’ultimo punto, consideriamo che
 è la somma di funzioni derivabili ovunque più la funzione
valore assoluto, che è non derivabile nell’origine perché qui vi
ha un punto angoloso. Quindi complessivamente
è la somma di funzioni derivabili ovunque più la funzione
valore assoluto, che è non derivabile nell’origine perché qui vi
ha un punto angoloso. Quindi complessivamente  non è derivabile nell’origine.
non è derivabile nell’origine.
Calcoliamo la derivata e uguagliamola a zero.
Per 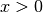 :
: 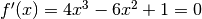 (cercheremo eventuali soluzioni positive).
Per
(cercheremo eventuali soluzioni positive).
Per 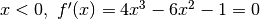 (soluzioni negative).
(soluzioni negative).
Soluzioni positive¶
Riscriviamo l’equazione come 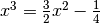 e cerchiamo
graficamente le intersezioni eventuali fra le due curve.
e cerchiamo
graficamente le intersezioni eventuali fra le due curve.
Si intuisce l’esistenza di due soluzioni, di cui la prima nell’intervallo
![[0,1]](../../../_images/math/ac2b83372f7b9e806a2486507ed051a8f0cab795.png) e la seconda nell’intervallo
e la seconda nell’intervallo ![[1,2]](../../../_images/math/852b7c03ed71e01ede864f0ce25f850429b19aad.png) . Ricaviamo la prima soluzione dal Teorema di Ruffini:
. Ricaviamo la prima soluzione dal Teorema di Ruffini: 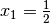 e la seconda abbassando il grado del polinomio:
e la seconda abbassando il grado del polinomio:
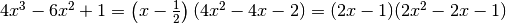 L’unica soluzione positiva di
L’unica soluzione positiva di 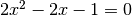 è
è
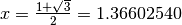 .
.
Soluzioni negative¶
L’equazione 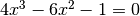 si può riscrivere come
si può riscrivere come
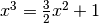 .
Il metodo del confronto fra i grafici è di aiuto per capire che non esistono
soluzioni negative, perché i due grafici non si intersecano per
.
Il metodo del confronto fra i grafici è di aiuto per capire che non esistono
soluzioni negative, perché i due grafici non si intersecano per  .
.
Il valore del minimo assoluto¶
Dobbiamo tener conto anche di 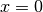 , dove la derivata non esiste.
Non resta che calcolare i valori di
, dove la derivata non esiste.
Non resta che calcolare i valori di  nei tre punti
che possono dare luogo ad un minimo assoluto.
nei tre punti
che possono dare luogo ad un minimo assoluto.
 . È quindi quest’ultimo
il valore minimo assoluto assunto dalla funzione.
. È quindi quest’ultimo
il valore minimo assoluto assunto dalla funzione.
Eventuali punti di massimo e minimo relativi e grafico¶
Abbiamo due punti da discutere: in  la derivata non esiste e in
la derivata non esiste e in
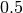 la derivata è nulla. Che tipo di punti sono questi, per
la derivata è nulla. Che tipo di punti sono questi, per  ?
Riguardando le considerazioni iniziali sulla continuità e sugli asintoti,
si può intuire che il primo sia un punto di minimo relativo, il secondo di massimo
relativo e per averne la prova basterebbe calcolare i valori di
?
Riguardando le considerazioni iniziali sulla continuità e sugli asintoti,
si può intuire che il primo sia un punto di minimo relativo, il secondo di massimo
relativo e per averne la prova basterebbe calcolare i valori di
 per
per  prossimi ai valori in discussione.
Possiamo però applicare le tecniche già apprese e procedere in modo
più completo ed elegante.
prossimi ai valori in discussione.
Possiamo però applicare le tecniche già apprese e procedere in modo
più completo ed elegante.
Per 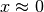 il polinomio
il polinomio 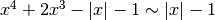 , che
è la funzione valore assoluto con il vertice in
, che
è la funzione valore assoluto con il vertice in 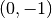 . Dunque, nella
monade di zero
. Dunque, nella
monade di zero 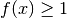 , il che corrisponde al fatto che per
, il che corrisponde al fatto che per 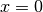
 ha un minimo relativo.
ha un minimo relativo.
Per studiare il comportamento (approssimato) di  per
per 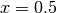 usiamo lo sviluppo in serie di Taylor del secondo ordine:
usiamo lo sviluppo in serie di Taylor del secondo ordine:
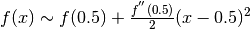 .
Calcolando
.
Calcolando 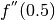 si ottiene
si ottiene 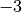 , quindi:
, quindi:
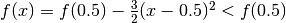 , quindi per
, quindi per 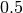 la funzione ha un massimo relativo.
la funzione ha un massimo relativo.
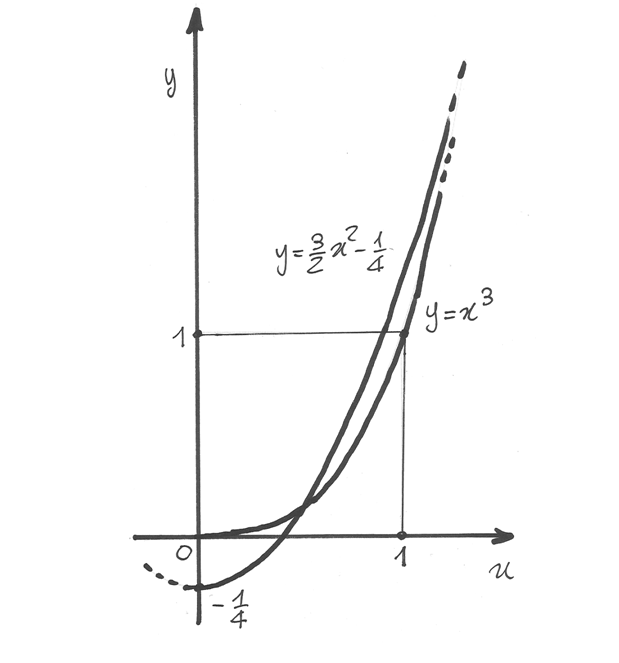
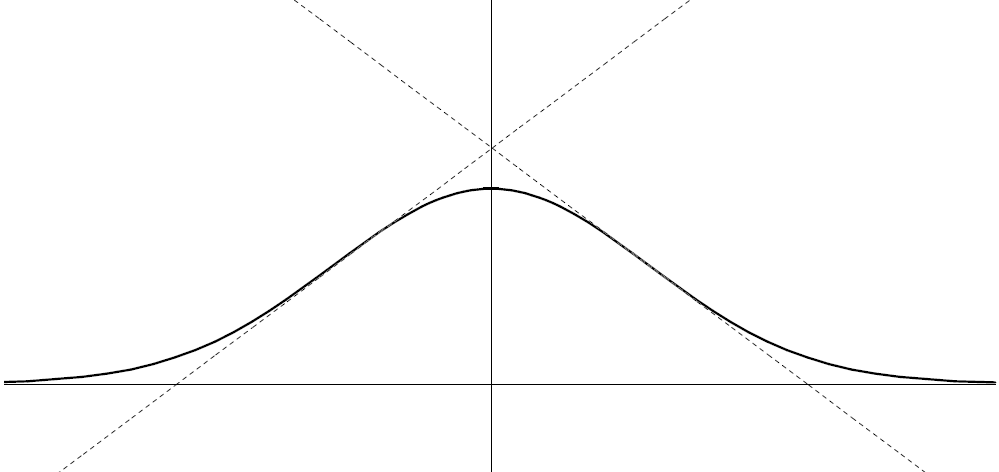
Ecco infatti il grafico della funzione, disegnato assieme ai grafici di
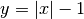 e di
e di 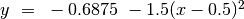 , che approssimano la
funzione negli ultimi due punti considerati.
, che approssimano la
funzione negli ultimi due punti considerati.
Considerazioni sulla derivata seconda¶
Gli ultimi calcoli, svolti con l’aiuto del polinomio di Taylor al secondo ordine, suggeriscono qualche ragionamento di grande utilità.
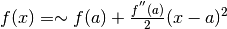 è l’espressione che vale
se
è l’espressione che vale
se 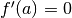 . Poiché
. Poiché 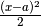 è un fattore positivo,
il segno della derivata seconda, calcolata in
è un fattore positivo,
il segno della derivata seconda, calcolata in  determina se
determina se
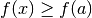 oppure
oppure 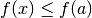 , e quindi se
, e quindi se  è
un punto di minimo o di massimo relativi. La procedura è:
è
un punto di minimo o di massimo relativi. La procedura è:
In un punto in cui la derivata prima si annulla, si controlla il segno della derivata seconda. Se in quel punto la derivata seconda è positiva, si tratta di un minimo relativo. Se invece è negativa, si tratta di un massimo relativo.
Se anche la derivata seconda si annulla¶
In questo caso la differenza 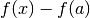 dipende dal termine del terzo
ordine del Polinomio di Taylor, perché
dipende dal termine del terzo
ordine del Polinomio di Taylor, perché
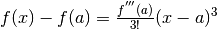 .
.
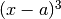 cambia segno a seconda che
cambia segno a seconda che  sia maggiore o minore di
sia maggiore o minore di  e, se la derivata terza è positiva,
e, se la derivata terza è positiva, 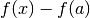 segue il segno di
segue il segno di 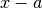 . In questo caso, cioè nel caso della derivata
terza positiva con le derivate prime e seconde nulle, il grafico della funzione
incrocia il grafico della tangente orizzontale nel punto
. In questo caso, cioè nel caso della derivata
terza positiva con le derivate prime e seconde nulle, il grafico della funzione
incrocia il grafico della tangente orizzontale nel punto 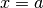 ,
passando da valori inferiori a sinistra di
,
passando da valori inferiori a sinistra di 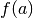 a valori superiori,
a destra. Si tratta quindi di una funzione crescente nell’intervallo, ma che
in
a valori superiori,
a destra. Si tratta quindi di una funzione crescente nell’intervallo, ma che
in  ha un punto a tangente orizzontale. Tale punto, che non è di massimo
o di minimo relativi, è chiamato punto di flesso orizzontale.
Se infine la derivata terza è negativa, con la derivata prima e seconda nulle,
possiamo svolgere considerazioni analoghe e individuare in
ha un punto a tangente orizzontale. Tale punto, che non è di massimo
o di minimo relativi, è chiamato punto di flesso orizzontale.
Se infine la derivata terza è negativa, con la derivata prima e seconda nulle,
possiamo svolgere considerazioni analoghe e individuare in  un
punto di flesso orizzontale di una funzione con andamento decrescente nell’intervallo.
un
punto di flesso orizzontale di una funzione con andamento decrescente nell’intervallo.
Se anche la derivata terza si annulla¶
In questo caso possiamo riprendere le considerazioni svolte al titolo precedente
perché il segno di 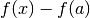 dipende dal termine del quarto ordine
del polinomio di Taylor. Se la derivata quarta è positiva abbiamo un minimo
relativo, altrimenti un massimo.
dipende dal termine del quarto ordine
del polinomio di Taylor. Se la derivata quarta è positiva abbiamo un minimo
relativo, altrimenti un massimo.
Regola generale In un punto dove si annullano le derivate prima e seconda, si calcolano le derivate successive fino alla prima derivata che non si annulla. Se questa derivata è di ordine pari, si svolgono le considerazioni già viste per la derivata seconda. Se questa derivata è di ordine dispari, siamo in presenza di un punto di flesso orizzontale.
Punti di flesso¶
Vengono chiamati flessi i cambi di concavità del grafico di una funzione. Nei punti di flesso la tangente al grafico sembra una retta secante: la funzione si avvicina al punto di tangenza per esempio da sinistra mantenendosi più bassa, cioè per valori inferiori, concava verso il basso; superato il punto di flesso troviamo la funzione dalla parte opposta della tangente, cioè con valori maggiori e concava verso l’alto. In questo caso si dice che il flesso è ascendente. Se invece a sinistra del punto di flesso la funzione è concava verso l’alto poi interseca la “tangente” e cambia concavità rivolgendosi verso il basso e assume valori inferiori alla tangente, allora il flesso si dice discendente. I flessi possono essere orizzontali, come già visto nell’esempio, oppure obliqui, nel senso che la retta tangente è inclinata. In questi casi la derivata prima nel punto in questione è diversa da zero.
L’equazione della tangente di  nel punto
nel punto  è
è
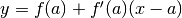 , come sappiamo. Si tratta del Polinomio
di Taylor del primo ordine.
La differenza fra i valori della funzione e quelli della tangente,
usando il Polinomio al secondo ordine, è
, come sappiamo. Si tratta del Polinomio
di Taylor del primo ordine.
La differenza fra i valori della funzione e quelli della tangente,
usando il Polinomio al secondo ordine, è
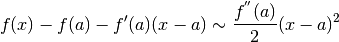
ed è una differenza che ha il segno di 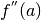 , purche sia
diversa da zero. Questo vuol dire che se per esempio il grafico della funzione
a sinistra di
, purche sia
diversa da zero. Questo vuol dire che se per esempio il grafico della funzione
a sinistra di  è tracciato sotto il grafico della tangente, allora
resta sotto anche a destra di
è tracciato sotto il grafico della tangente, allora
resta sotto anche a destra di  .
Se invece la derivata seconda è nulla e la derivata terza no, scriviamo
.
Se invece la derivata seconda è nulla e la derivata terza no, scriviamo
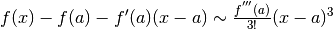 , che, come
abbiamo già visto, cambia segno in relazione a
, che, come
abbiamo già visto, cambia segno in relazione a 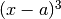 , il
che costringe il grafico della funzione a scavalcare la retta “tangente”.
, il
che costringe il grafico della funzione a scavalcare la retta “tangente”.
Criterio delle derivate successive¶
Se per 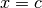 si annulla la derivata seconda
si annulla la derivata seconda 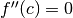 , calcola
, calcola
 derivate successive, fino alla prima derivata
derivate successive, fino alla prima derivata 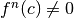 e controlla:
e controlla:
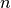 è dispari:
allora
è dispari:
allora 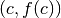 è un punto di flesso.
Se
è un punto di flesso.
Se 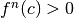 il flesso è ascendente, altrimenti è un flesso discendente.
Se inoltre anche
il flesso è ascendente, altrimenti è un flesso discendente.
Se inoltre anche 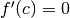 il flesso è orizzontale (ascendente o discendente).
il flesso è orizzontale (ascendente o discendente).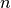 è pari:
è pari:non avremo un flesso, ma solo indicazioni sulla concavità.
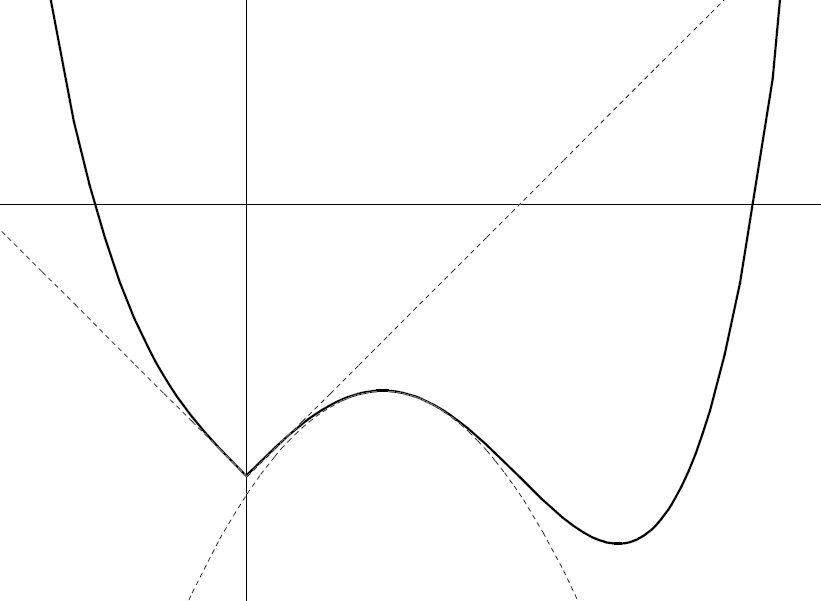
I flessi per l’esempio 1¶
Concludiamo l’esercizio precedente con la ricerca dei flessi.
Cerchiamo quindi dove si annulla la derivata seconda e se in quel
punto la prima derivata non nulla è di ordine dispari.
Abbiamo per 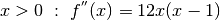 , che si annulla per
, che si annulla per
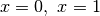 . Escludiamo :
. Escludiamo :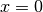 , dove
, dove  non è derivabile,
e calcoliamo
non è derivabile,
e calcoliamo 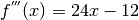 quindi
quindi 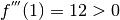 .
Si tratta quindi di un flesso ascendente.
.
Si tratta quindi di un flesso ascendente.
Si può controllare che per  le uniche soluzioni possibili non sono accettabili.
le uniche soluzioni possibili non sono accettabili.
Esempio 2¶
Individuiamo i flessi per la funzione statistica della distribuzione normale
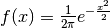
Cerchiamo quindi i punti per i quali si annulla la derivata seconda, ma non la derivata terza.
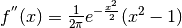 , che si annulla
per
, che si annulla
per 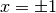
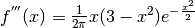 , positiva per
, positiva per
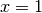 (flesso ascendente) e negativa per
(flesso ascendente) e negativa per 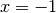 (flesso discendente)
come è prevedibile per la parità della funzione.
(flesso discendente)
come è prevedibile per la parità della funzione.
Terzo problema di ottimizzazione¶
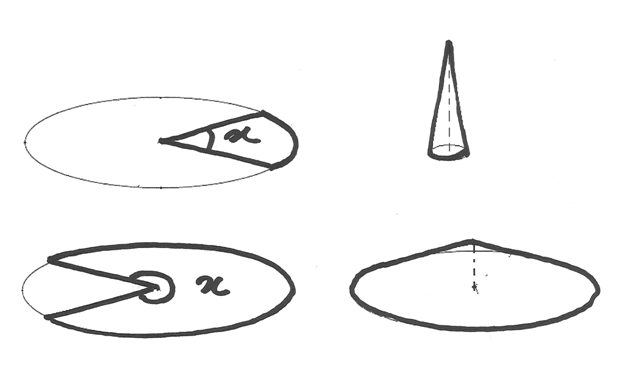
Si vuole ritagliare un disco di raggio dato 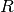 per farne un settore
circolare da vvolgere in modo da ottenere un cono. Calcolare il settore utile
a generare il cono più capiente.
per farne un settore
circolare da vvolgere in modo da ottenere un cono. Calcolare il settore utile
a generare il cono più capiente.
Se il settore che si ricava è sottile, il cono è eccessivamente stretto e
poco capiente. Lo stesso avviene per un settore eccessivamente largo, che genera un
cono troppo basso. Esiste quindi una misura intermedia ottimale di angolo
al centro  , che corrisponde al volume massimo del cono.
Occorre trovare la relazione che lega l’angolo (in radianti) al volume
del cono.
, che corrisponde al volume massimo del cono.
Occorre trovare la relazione che lega l’angolo (in radianti) al volume
del cono.
La formula del volume del cono è 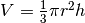 , dove
, dove  è il raggio di base del cono che si genera. Questo raggio è legato alla circonferenza
è il raggio di base del cono che si genera. Questo raggio è legato alla circonferenza
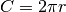 , che è l’arco del settore circolare. Quindi
, che è l’arco del settore circolare. Quindi
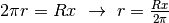 .
.
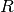 , il raggio del disco, nel cono diventa l’apotema. Questo ci consente di ricavare l’altezza
, il raggio del disco, nel cono diventa l’apotema. Questo ci consente di ricavare l’altezza 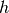 del cono:
del cono: 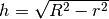 .
.
La funzione da ottimizzare, che esprime il volume in funzione dell’angolo  è
è
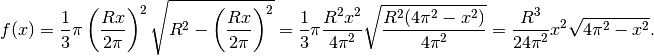
La variazione della funzione è data dal variare di 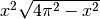 ,
che chiameremo
,
che chiameremo 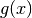 , mentre il fattore
, mentre il fattore 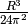 è una costante che cambia i valori della funzione ma non influisce sugli
è una costante che cambia i valori della funzione ma non influisce sugli
 per i quali si ha il volume massimo. Infatti
per i quali si ha il volume massimo. Infatti 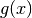 e
e  sono direttamente proporzionali. Anzi, per rendere ancora più veloce l’individuazione
del punto di massimo, possiamo considerare
sono direttamente proporzionali. Anzi, per rendere ancora più veloce l’individuazione
del punto di massimo, possiamo considerare 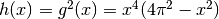 .
.
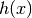 e
e 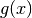 sono entrambe definite su
sono entrambe definite su ![[0,2\pi]](../../../_images/math/afd1cc9f6085210dc7aea0e591b90df796cff56c.png) , sono continue
e derivabili all’interno dell’intervallo, sono nulle agli estremi e raggiungono
il massimo assoluto per lo stesso
, sono continue
e derivabili all’interno dell’intervallo, sono nulle agli estremi e raggiungono
il massimo assoluto per lo stesso 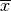 , ovviamente con valori
che sono uno il quadrato dell’altro.
, ovviamente con valori
che sono uno il quadrato dell’altro.
Dal punto di vista concreto, non dovremmo considerare praticabili angoli come
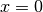 e
e 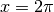 , ma includiamo ugualmente questi valori come estremi
perché definire la funzione sull’intervallo chiuso e limitato è una delle condizioni
che garantiscono l’esistenza del massimo assoluto. Data la situazione, escludiamo
che il punto di massimo sia un estremo dell’intervallo e cerchiamo quindi solo
i punti interni per i quali si annulla la derivata.
, ma includiamo ugualmente questi valori come estremi
perché definire la funzione sull’intervallo chiuso e limitato è una delle condizioni
che garantiscono l’esistenza del massimo assoluto. Data la situazione, escludiamo
che il punto di massimo sia un estremo dell’intervallo e cerchiamo quindi solo
i punti interni per i quali si annulla la derivata.
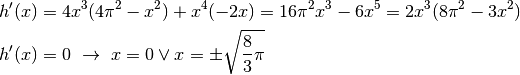
L’unica soluzione accettabile è l’ultima, positiva, e di conseguenza
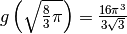 e
e
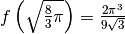 .
Per avere una risposta concreta, vediamo quanto valgono in gradi
.
Per avere una risposta concreta, vediamo quanto valgono in gradi
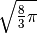 radianti.
radianti.
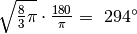 .
.
Usiamo le formule iniziali per ricavare il raggio
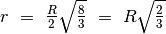 e l’altezza
e l’altezza
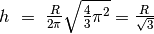 del cono ottimale.
Ne consegue che il cono ottimale ha il raggio di base che è
del cono ottimale.
Ne consegue che il cono ottimale ha il raggio di base che è 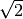 volte l’altezza.
volte l’altezza.
Riassunto¶
- I massimi e i minimi di una funzione sono i valori estremi che la funzione raggiunge in un intervallo. I massimi, come i minimi, possono essere assoluti o relativi. Sono assoluti quando sono i valori maggiori (i minori), considerando tutto l’intervallo di definizione. Sono relativi se questo avviene considerando intervalli ristretti attorno ai punti in questione. I massimi (minimi) assoluti sono anche massimi (minimi) relativi, mentre non vale il contrario.
- Una funzione, continua o discontinua, può avere nessuno, uno, alcuni o infiniti massimi (minimi) assoluti e relativi.
- L’esistenza di un massimo (minimo) assoluto è garantita per le funzioni continue definite su un intervallo chiuso e limitato, per i punti interni all’intervallo. Non è garantita agli estremi dell’intervallo e per le funzioni discontinue.
- Nelle condizioni del punto precedente, in almeno un punto la
derivata prima della funzione è nulla. Calcolare per quali
 la
la
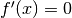 è la prima strategia alla quale ricorrere per trovare i punti
di massimo e di minimo.
è la prima strategia alla quale ricorrere per trovare i punti
di massimo e di minimo. - Quando si annulla la derivata prima, si può indagare ulteriormente per capire la natura del punto in questione. Se in quel punto la derivata seconda è positiva, il grafico ha una concavità verso l’alto e siamo in presenza di un minimo, se è negativa la concavità è verso il basso e siamo in presenza di un massimo.
- La derivata prima si annulla anche nei punti di flesso orizzontale, che sono i punti in cui il grafico della funzione cambia concavità. In questo caso anche la derivata seconda si annulla nel punto.
- Il criterio delle derivate successive (17.6) consente in generale di individuare massimi, minimi e flessi delle funzioni pìù volte derivabili nell’intervallo (estremi esclusi)
Esercizi¶
- La capacità della scatola calcolata nel primo esempio del capitolo è di 1.13 litri. Quale è la misura del taglio che genera una scatola con la capacità di 1 litro? Scrivi l’equazione risolvente e applica i metodi approssimati per risolverla.
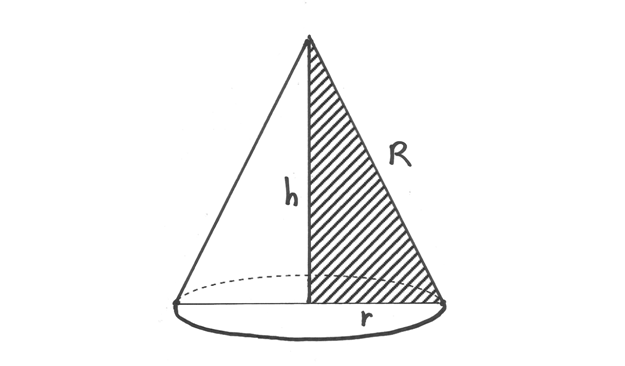
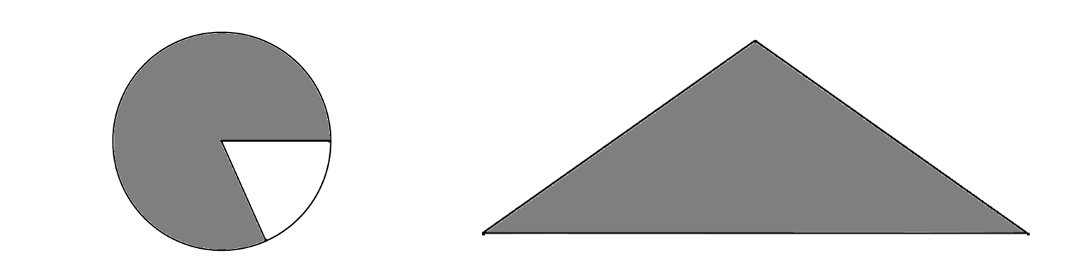
 . Ne risulta una sezione conica verticale come in figura.
. Ne risulta una sezione conica verticale come in figura.