I grafici delle funzioni¶
In quest’ultimo capitolo utilizziamo le conoscenze già viste, precisandole e approfondendole, e ne sviluppiamo di nuove per imparare a disegnare manualmente il grafico di una funzione. Molti software matematici, alcuni anche gratuiti e online, e molte calcolatrici scientifiche sono oggi in grado di svolgere perfettamente questo compito. Lasceremo a questi utili strumenti di calcolo la parte più macchinosa e meno attraente e terremo per noi la parte più nobile del compito, cioè la previsione e la valutazione delle proprietà del risultato.
Dettagli sul dominio¶
Finora abbiamo usato come dominio delle funzioni gli intervalli di numeri
![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , oppure
, oppure 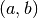 , o
, o 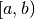 , o infine
, o infine ![(a,b]](../../../_images/math/d17f423539959c57aad1c20cb6c7ed9ccfee4f65.png) .
Con queste notazioni puntiamo l’attenzione sui numeri
.
Con queste notazioni puntiamo l’attenzione sui numeri 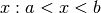 interni
all’intervallo e sottintendiamo che i numeri
interni
all’intervallo e sottintendiamo che i numeri 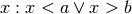 siano esterni
e che infine
siano esterni
e che infine 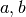 siano i punti di frontiera del dominio.
Trattandosi di numeri iperreali, cioè di numeri sui
quali dobbiamo poter indagare anche con microscopi non standard, dobbiamo
precisare alcune cose, che riprendiamo dal primo volume.
siano i punti di frontiera del dominio.
Trattandosi di numeri iperreali, cioè di numeri sui
quali dobbiamo poter indagare anche con microscopi non standard, dobbiamo
precisare alcune cose, che riprendiamo dal primo volume.
Una volta individuata la proprietà caratteristica di un intervallo
della retta reale, sappiamo definire per estensione l’intervallo corrispondente
di iperreali: si tratta dei numeri 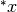 che hanno la stessa proprietà.
Per esempio da un intervallo di reali
che hanno la stessa proprietà.
Per esempio da un intervallo di reali 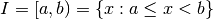 passiamo
a
passiamo
a 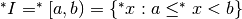 di iperreali.
di iperreali.
Sappiamo anche che ogni funzione reale di numeri reali 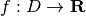 ha una corrispondente funzione
ha una corrispondente funzione 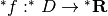 iperreale di
numeri iperreali e che rinunciamo a scrivere cose come
iperreale di
numeri iperreali e che rinunciamo a scrivere cose come  oppure
oppure 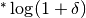 per semplicità e perché diamo per scontato che
se l’argomento è un numero non standard allora stiamo usando l’estensione iperreale
della funzione.
per semplicità e perché diamo per scontato che
se l’argomento è un numero non standard allora stiamo usando l’estensione iperreale
della funzione.
Classificazione dei punti del dominio¶
Dato un intervallo 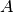 e il suo complemento
e il suo complemento 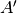 di reali, consideriamo
le estensioni iperreali
di reali, consideriamo
le estensioni iperreali 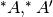 . Chiamiamo
. Chiamiamo
- punti interni di
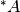 quelli per cui
quelli per cui 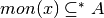 , cioè
i punti che intendiamo siano contenuti in
, cioè
i punti che intendiamo siano contenuti in 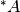 con la propria monade
con la propria monade - punti esterni di
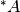 quelli per cui
quelli per cui 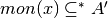 , la cui
monade non è contenuta a
, la cui
monade non è contenuta a 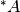
- punti di frontiera per
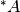 quelli per cui
quelli per cui
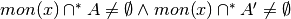 ,
nella cui monade ci sono sia punti di
,
nella cui monade ci sono sia punti di 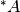 che punti del suo complemento
che punti del suo complemento 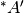
I punti possono essere solo in una di queste tre situazioni, rispetto a 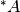 .
.
Quando studiamo il comportamento asintotico di una funzione in un punto, in realtà
siamo interessati ai valori che la funzione assume nei punti infinitamente vicini,
quindi diversi dal punto indicato. Per esempio 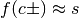 significa
significa
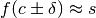 , cioè
, cioè 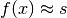 per tutti gli
per tutti gli  infinitamente vicini a
infinitamente vicini a  , ma in generale diversi da
, ma in generale diversi da  . Infatti
può anche succedere che la funzione non sia definita per
. Infatti
può anche succedere che la funzione non sia definita per 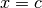 , mentre
deve esserlo per
, mentre
deve esserlo per 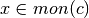 .
È il caso tipico dei punti di frontiera degli intervalli aperti di iperreali,
per i quali ci aspettiamo che la funzione sia definita per la monade destra di
.
È il caso tipico dei punti di frontiera degli intervalli aperti di iperreali,
per i quali ci aspettiamo che la funzione sia definita per la monade destra di
 e per quella sinistra di
e per quella sinistra di 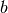 .
A volte invece non possiamo studiare il comportamento asintotico della funzione
per
.
A volte invece non possiamo studiare il comportamento asintotico della funzione
per 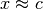 perché
solo
perché
solo  appartiene a
appartiene a 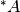 e non la sua monade, o meglio
e non la sua monade, o meglio
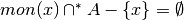 . Allora si dice che siamo in presenza di
un punto isolato.
. Allora si dice che siamo in presenza di
un punto isolato.
- punti isolati di
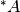 quei punti di frontiera per cui
quei punti di frontiera per cui 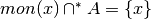 ,
cioè essi sono gli unici elementi comuni sia alla propria monade che all’estensione
di
,
cioè essi sono gli unici elementi comuni sia alla propria monade che all’estensione
di 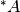 .
.
In conclusione, è possibile studiare il comportamento asintotico di  solo per i punti interni di
solo per i punti interni di 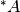 e per i punti di frontiera non isolati,
perché in entrambi i casi
e per i punti di frontiera non isolati,
perché in entrambi i casi 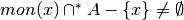 .
Questi punti sono quelli utili per noi ed hanno un nome particolare:
.
Questi punti sono quelli utili per noi ed hanno un nome particolare:
- punti di accumulazione di
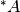 quei punti per cui
quei punti per cui
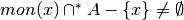 , cioè punti per i quali ogni monade
contiene dell’estensione di
, cioè punti per i quali ogni monade
contiene dell’estensione di 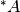 almeno un punto diverso
almeno un punto diverso  .
.
Perciò se  è un punto di accumulazione per il dominio
è un punto di accumulazione per il dominio 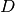 di
di
 , possiamo dire che
, possiamo dire che 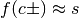 se
se
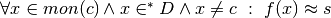 .
.
Per esempio, se accade che 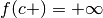 , si dirà che
, si dirà che  è un
punto di accumulazione destro per il quale la funzione è un infinito positivo.
è un
punto di accumulazione destro per il quale la funzione è un infinito positivo.
Esercizio¶
Dato l’insieme 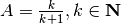 , definisci l’estensione
di
, definisci l’estensione
di 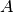 , i suoi punti interni, esterni, isolati, di frontiera di accumulazione.
, i suoi punti interni, esterni, isolati, di frontiera di accumulazione.
L’estensione 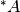 si ottiene per
si ottiene per  ipernaturale infinito,
quindi aggiungendo i punti
ipernaturale infinito,
quindi aggiungendo i punti 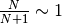 . Quindi
. Quindi 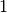 è un
punto di accumulazione per l’insieme
è un
punto di accumulazione per l’insieme 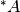 , mentre gli altri punti,
che si ottengono per
, mentre gli altri punti,
che si ottengono per  finito, nelle loro monadi non hanno altri elementi
dell’insieme esteso . Sono punti isolati e dunque sono punti di frontiera.
Abbiamo quindi un insieme costituito da infiniti punti di frontiera, uno dei quali
è anche di accumulazione: un insieme senza punti interni.
finito, nelle loro monadi non hanno altri elementi
dell’insieme esteso . Sono punti isolati e dunque sono punti di frontiera.
Abbiamo quindi un insieme costituito da infiniti punti di frontiera, uno dei quali
è anche di accumulazione: un insieme senza punti interni.
Note
Un punto che appartiene ad un insieme non è detto che sia interno all’insieme. All’insieme appartengono i punti interni e quelli di frontiera, fra i quali anche quelli isolati.
Immaginiamo che 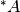 sia il dominio della funzione
sia il dominio della funzione
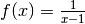 . Possiamo studiare il comportamento asintotico di
. Possiamo studiare il comportamento asintotico di  solo per
solo per 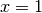 , cioè per i punti
, cioè per i punti 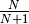 infinitamente vicini
a
infinitamente vicini
a 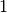 e diversi da
e diversi da 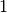 . Infatti
. Infatti 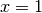 è l’unico punto di accumulazione.
è l’unico punto di accumulazione.
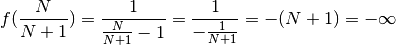
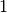 è il punto di accumulazione sinistro per cui
è il punto di accumulazione sinistro per cui  è un infinito negativo.
Si può ottenere lo stesso risultato valutando
è un infinito negativo.
Si può ottenere lo stesso risultato valutando 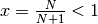 e
quindi
e
quindi 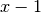 è un infinito negativo.
è un infinito negativo.
In aggiunta, osserviamo che il differenziale 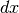 non è calcolabile
(e quindi nemmeno la derivata), perché mancano punti interni al dominio.
non è calcolabile
(e quindi nemmeno la derivata), perché mancano punti interni al dominio.
Uno studio di funzione completo: esercizio guida¶
Sappiamo già come ricavare parecchie indicazioni sul grafico di una funzione. Sappiamo che la derivata prima ci dice se la funzione è crescente o decrescente, che i punti a derivata nulla sono o di massimo o di minimo o di flesso orizzontale, che il segno della derivata seconda ci indica la concavità. Inoltre se la prima delle derivate successive non nulle è di ordine dispari avremo un flesso ascendente per la derivata positiva (quindi funzione crescente), altrimenti discendente (quindi decrescente).
Per applicare le nostre conoscenze e completarle eseguiamo lo studio di
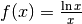
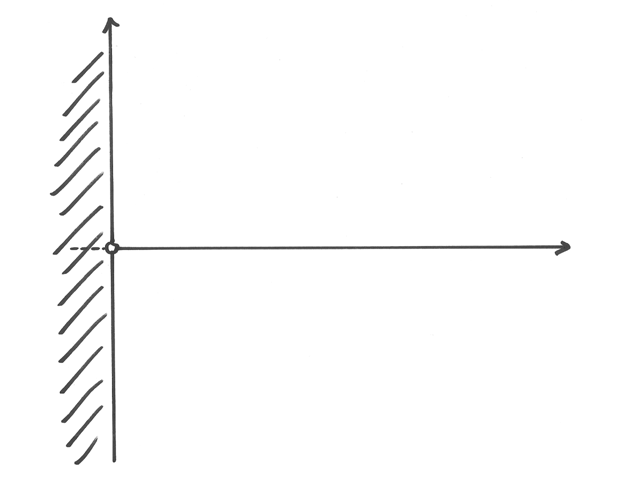
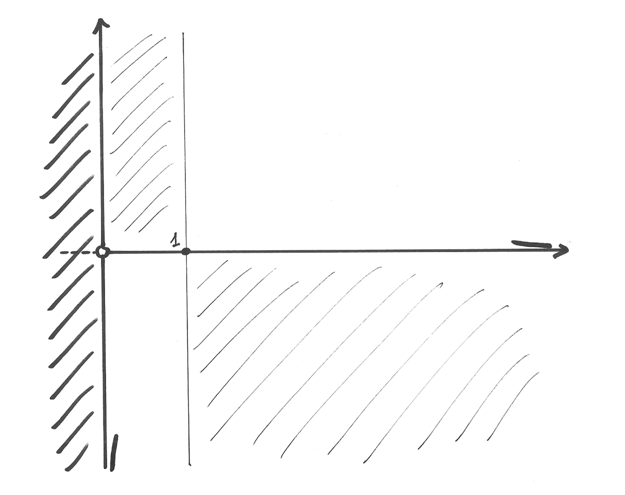
Il dominio¶
Il dominio è parte integrante della definizione della funzione e se non viene
esplicitamente indicato si assume che sia il più ampio intervallo di reali per i
quali la funzione ha significato. La nostra  non è calcolabile se il
denominatore è zero e in più il numeratore è definito per valori
non è calcolabile se il
denominatore è zero e in più il numeratore è definito per valori  positivi.
Le due condizioni (di esistenza) sono quindi
positivi.
Le due condizioni (di esistenza) sono quindi

Il disegno corrispondente è il semipiano positivo, intendendo escluso anche
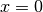 , punto nel quale disegniamo un cerchietto vuoto.
, punto nel quale disegniamo un cerchietto vuoto.
La simmetria¶
Si cerca di stabilire se la funzioni ha simmetria. Ricordiamo
- Se
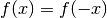 la funzione è pari e il suo grafico è simmetrico
rispetto all’asse
la funzione è pari e il suo grafico è simmetrico
rispetto all’asse 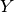 .
. - Se
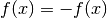 la funzione è dispari e il suo grafico è simmetrico
rispetto all’origine.
la funzione è dispari e il suo grafico è simmetrico
rispetto all’origine.  non è né pari né dispari: nessuna di queste simmetrie.
non è né pari né dispari: nessuna di queste simmetrie.
Per il controllo della simmetria conviene calcolare 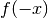 , cioè sostituire
, cioè sostituire
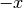 ad
ad  nell’espressione della funzione, e controllare a quale
delle opzioni corrisponde il risultato. La nostra funzione non ha simmetria e lo
si vede già disegnando il dominio.
nell’espressione della funzione, e controllare a quale
delle opzioni corrisponde il risultato. La nostra funzione non ha simmetria e lo
si vede già disegnando il dominio.
Note
 può avere altre simmetrie, come si vedrà nell’ultimo esercizio
del capitolo. L’analisi di tutte le possibili simmetrie si può fare negli esercizi
in cui si parte dal grafico per analizzare le proprietà della funzione ed è
di grande aiuto perché abbrevia il lavoro.
può avere altre simmetrie, come si vedrà nell’ultimo esercizio
del capitolo. L’analisi di tutte le possibili simmetrie si può fare negli esercizi
in cui si parte dal grafico per analizzare le proprietà della funzione ed è
di grande aiuto perché abbrevia il lavoro.
Le intersezioni¶
Per avere punti di riferimento nel disegno la strategia più semplice è cercare
le intersezioni del grafico con gli assi. .
È meglio cercare dapprima le intersezioni con l’asse 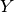 , infatti le
intersezioni con l’asse
, infatti le
intersezioni con l’asse  sono i punti per i quali
sono i punti per i quali 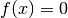 e
non è sempre semplice trovare le soluzioni, che possono anche essere infinite.
e
non è sempre semplice trovare le soluzioni, che possono anche essere infinite.
Intersezioni con l’asse 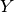 : nel nostro caso non esistono perché
: nel nostro caso non esistono perché
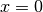 è escluso da dominio.
è escluso da dominio.
Intersezioni con l’asse 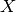 : le intersezioni per
: le intersezioni per 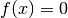 corrispondono alle soluzioni di
corrispondono alle soluzioni di 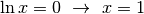 .
Abbiamo una sola intersezione, in
.
Abbiamo una sola intersezione, in 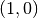 .
.
Il segno¶
Non sappiamo se a sinistra dell’intersezione il grafico sia nel primo
o nel quarto quadrante e non sappiamo se intersecando l’asse orizzontale il
grafico cambi o no quadrante. Per questo motivo cerchiamo di risolvere 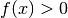 .
.
Se la ricerca delle soluzioni è particolarmente complessa, per le funzioni continue
possiamo anche evitarla: basterà calcolare il valore di  in punto fra due
intersezioni consecutive, infatti fra due zeri consecutivi una funzione continua
ha segno costante, altrimenti vi sarebbero ulteriori intersezioni fra i due punti .
in punto fra due
intersezioni consecutive, infatti fra due zeri consecutivi una funzione continua
ha segno costante, altrimenti vi sarebbero ulteriori intersezioni fra i due punti .
Ma il nostro è un caso semplice: dato che il dominio è per 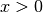 , la funzione
ha lo stesso segno del logaritmo, cioè
, la funzione
ha lo stesso segno del logaritmo, cioè
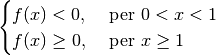
Cancelliamo dal disegno le regioni del piano non attraversate dal grafico.
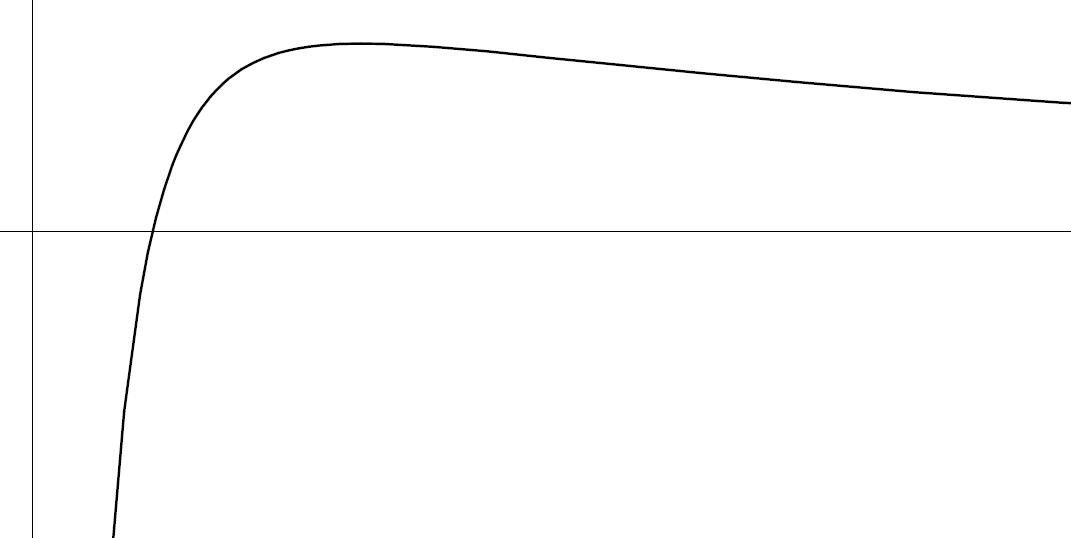
Gli asintoti¶
Se nel dominio vi sono punti di frontiera che sono anche di accumulazione e se vi
sono punti infiniti, occorre capire il comportamento asintotico di  .
Nel notro caso occorre calcolare
.
Nel notro caso occorre calcolare 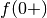 e
e 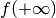 .
.
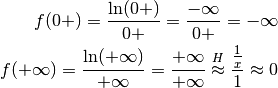
Abbiamo quindi un asintoto vertivale in 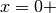 e uno orizzontale in
e uno orizzontale in
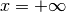 . Nel grafico aggiungiamo due piccoli tratti a sinistra in basso e
a destra appena sopra l’asse orizzontle, per ricordarci dove passerà il disegno.
. Nel grafico aggiungiamo due piccoli tratti a sinistra in basso e
a destra appena sopra l’asse orizzontle, per ricordarci dove passerà il disegno.
L’andamento¶
Il segno della derivata prima ci dirà se e in quali intervalli la funzione è crescente o decrescente; se si annulla cercheremo di capire in quali punti vi può essere un massimo o un minimo o un flesso orizzontale.
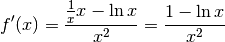
si annulla per 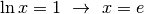 .
Che ci fosse un punto a tangente orizzontale era prevedibile, dopo lo studio del
comportamento asintotico, e resta solo da capire se e dove
.
Che ci fosse un punto a tangente orizzontale era prevedibile, dopo lo studio del
comportamento asintotico, e resta solo da capire se e dove  è crescente o decrescente, anche se ormai si intuisce, dato che nel dominio è continua.
è crescente o decrescente, anche se ormai si intuisce, dato che nel dominio è continua.
In generale può essere molto complicato risolvere 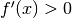 e allora
è consigliabile procedere come indicato per
e allora
è consigliabile procedere come indicato per 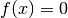 , sempre che la
derivata sia continua.
Nel nostro caso la disequazione è semplice:
, sempre che la
derivata sia continua.
Nel nostro caso la disequazione è semplice:
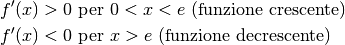
La funzione raggiunge quindi in 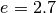 il suo massimo (assoluto), con il valore
il suo massimo (assoluto), con il valore
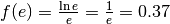 e poi decresce adagiandosi progressivamente
sull’asse
e poi decresce adagiandosi progressivamente
sull’asse 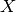 .
.
La concavità e i flessi¶
È evidente che approssimandosi al massimo  ha la concavità rivolta
verso il basso e che per adagiarsi sull’asse orizzontale subisce un cambio di concavità.
Analizziamo i dettagli con lo studio della derivata seconda.
ha la concavità rivolta
verso il basso e che per adagiarsi sull’asse orizzontale subisce un cambio di concavità.
Analizziamo i dettagli con lo studio della derivata seconda.
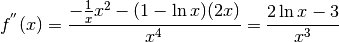
che si annulla per 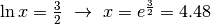 .
.
Il segno della derivata seconda, se la sua espressione è complicata ma la derivata è continua, si può ricavare seguendo i suggerimenti analoghi visti per per il segno della funzione e della derivata prima.
Il nostro caso però è di quelli semplici:
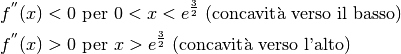
per cui in 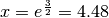 la funzione ha un flesso ascendente,
con il valore di
la funzione ha un flesso ascendente,
con il valore di 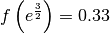 .
Inoltre la derivata seconda ci conferma che
.
Inoltre la derivata seconda ci conferma che 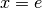 è un punto di massimo, perché
è un punto di massimo, perché
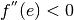 .
.
Le conclusioni sul flesso ascendente si possono verificare anche con la derivata terza,
perché 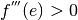
Nei casi complicati, in cui le equazioni 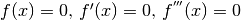 e le disequazioni associate sono troppo laboriose, ci si affida ai software che
tracciano i grafici automaticamente.
e le disequazioni associate sono troppo laboriose, ci si affida ai software che
tracciano i grafici automaticamente.
Tuttavia questi strumenti a volte non chiariscono le esatte posizioni dei punti caratteristici ed occorre comunque aiutarsi con i calcoli.
La curvatura¶
Quando il grafico è stato tracciato manualmente, resta sempre il dubbio di non avere tracciato correttamete le curve fra i punti notevoli calcolati. Cerchiamo di costruire un metodo per identificare la curvatura che il grafico corretto deve seguire in ogni punto: avremo così uno strumento di analisi e di confronto anche per le curvature disegnate dal software.
La curvatura più facile da analizzare è quella di un cerchio. Chi lo percorre
stando sulla circonferenza deve cambiare la sua direzione di un angolo pari
all’angolo spazzato dal raggio. La direzione punto per punto è data dalla direzione
della tangente e la curvatura è costante, per ogni cerchio. C’è infatti un rapporto
fisso fra l’arco di circonferenza percorso 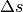 e l’angolo al centro
(misurato in radianti)
e l’angolo al centro
(misurato in radianti) 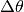 , che è dato dal raggio:
, che è dato dal raggio:
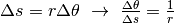 .
La curvatura è la rapidità con cui si cambia direzione percorrendo l’arco e
quindi è il rapporto fra angolo e arco, inversamente proporzionale al raggio.
La relazione vale anche per archi infinitesimi:
.
La curvatura è la rapidità con cui si cambia direzione percorrendo l’arco e
quindi è il rapporto fra angolo e arco, inversamente proporzionale al raggio.
La relazione vale anche per archi infinitesimi:
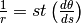 .
.
Cerchiamo ora di adattare questi risultati iniziali a grafici con curvature qualsiasi. Il procedimento generalizza e precisa quanto già visto a proposito della ricerca del cerchio osculatore di una curva, nel libro precedente.
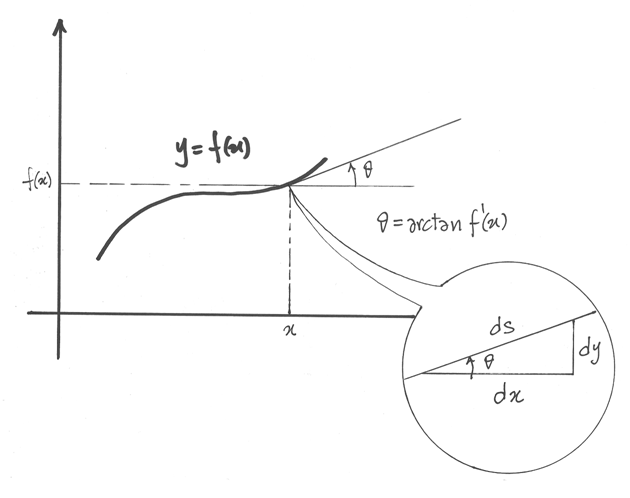
Tracciamo in  la tangente al grafico: sarà una retta inclinata di un angolo
la tangente al grafico: sarà una retta inclinata di un angolo
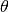 rispetto all’orizzontale, la cui tangente goniometrica
è la derivata della funzione in
rispetto all’orizzontale, la cui tangente goniometrica
è la derivata della funzione in  :
: 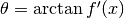 .
.
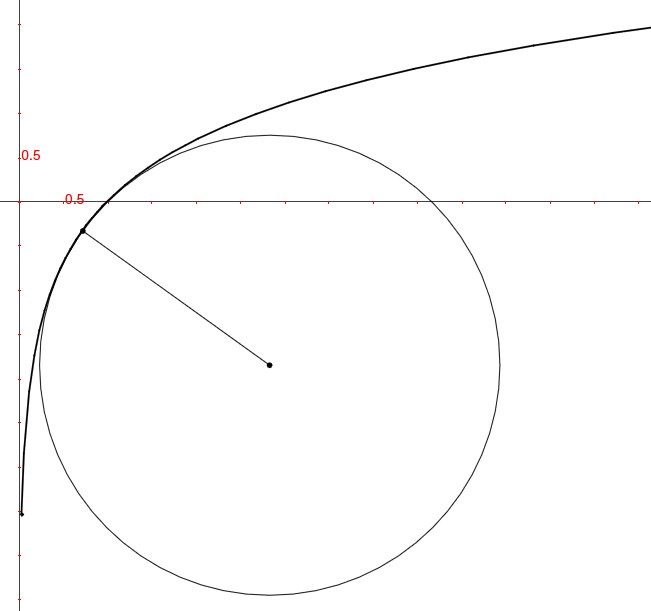
Per esempio, calcoliamo il raggio del cerchio osculatore alla parabola
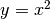 nel punto
nel punto 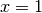 .
.
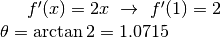 , cioè circa
, cioè circa 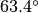
Il calcolo non è finito, perché la derivata che abbiamo calcolato
è 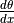 e non
e non 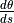 .
. 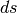 è
il tratto infinitesimo di curva. Osservato al microscopio non standard, poiché
è
il tratto infinitesimo di curva. Osservato al microscopio non standard, poiché
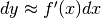 , risulta
, risulta
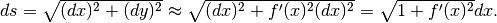
L’angolo (in radianti) è l’arcotangente di 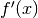 , perciò
abbiamo:
, perciò
abbiamo: 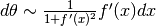 e quindi:
e quindi:
![&\frac{d\theta}{ds}=\frac{\frac{f^{''}(x)}{1+f'(x)^2}dx}{\sqrt{1+f'(x)^2}dx}
=\frac{f^{''}(x)}{\left[1+f'(x)^2\right]^\frac{3}{2}}=\frac{1}{r(x)}\\
&r(x)=\frac{\left[1+f'(x)^2\right]^\frac{3}{2}}{f^{''}(x)}](../../../_images/math/cf455acd57d356cbde3194d31e457490f3bf7aa2.png)
Il raggio in questo modo potrebbe anche risultare negativo, dipendendo dal segno di
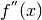 . Il raggio negativo indicherà la curvatura concava verso il basso, il raggio positivo indicherà la curvatura verso l’alto.
. Il raggio negativo indicherà la curvatura concava verso il basso, il raggio positivo indicherà la curvatura verso l’alto.
Tornando alla parabola, applicando la formula il raggio risulta
![r(x)=\frac{\left[1+4x^2\right]^\frac{3}{2}}{2}](../../../_images/math/d4d5022d5e9eac6ca7a3634e6afaea32af39514e.png) .
Quindi al suo vertice la curvatura della parabola ha un raggio di
.
Quindi al suo vertice la curvatura della parabola ha un raggio di
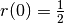 , che corrisponde al risultato ottenuto nel primo libro.
, che corrisponde al risultato ottenuto nel primo libro.
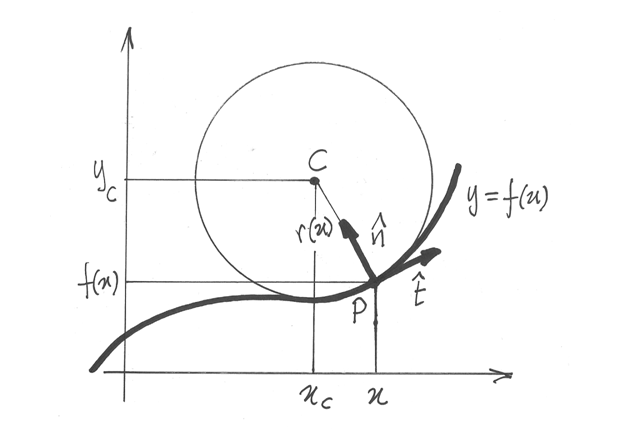
Ora è facile disegnare il cerchio osculatore al vertice della parabola. La formula però è utile per disegnare il cerchio in qualsiasi punto della curva, purché si sappia in quale posizione fissare il centro. Vediamo come trovare la posizione del centro.
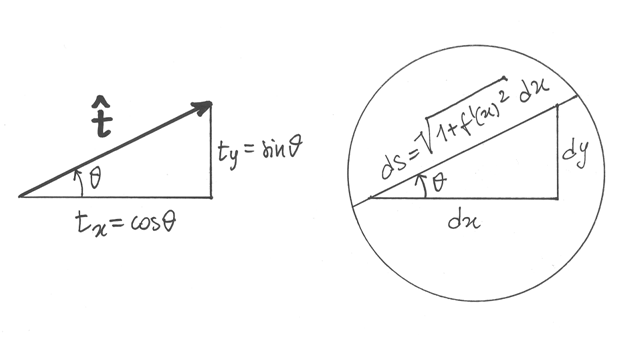
La direzione della tangente si può rappresentare tramite il versore  che punta nella direzione positiva degli assi. Le sue componenti, secondo il coseno
e il seno dell’angolo, sono
che punta nella direzione positiva degli assi. Le sue componenti, secondo il coseno
e il seno dell’angolo, sono
Trovate le componenti del versore tangente, calcoliamo quelle del versore 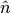 perpendicolare alla curva in quel punto. Dato che il raggio è perpendicolare
alla tangente,
perpendicolare alla curva in quel punto. Dato che il raggio è perpendicolare
alla tangente, 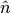 punta al centro del cerchio osculatore.
Abbiamo
punta al centro del cerchio osculatore.
Abbiamo
Trovata la direzione del centro, la sua posizione si ottiene moltiplicando le componenti del versore normale per la lunghezza del raggio.
Operate le sostituzioni e svolti i calcoli, risulta:
![\begin{cases}
& x_c=x-\frac{f'(x)\left[1+f'(x)^2\right]}{f^{''}(x)} \\
& y_c=f(x)+\frac{1+f'(x)^2}{f^{''}(x)}
\end{cases}](../../../_images/math/a82e8e6172390fb4c9695c3f36e62c07e7b6da99.png)
che sono le coordinate del centro del cerchio osculatore, relative a qualsiasi punto del grafico e per qualsiasi concavità, purché, ovviamente, la derivata seconda non si annulli. In questo caso non vi sarebbe nessuna concavità e il cerchio osculatore avrebbe un raggio infinito.
Applichiamo le due formule alla solita parabola, per trovare il centro
del cerchio osculatore relativo al punto di ascissa  . Una volta svolti
i calcoli avremo:
. Una volta svolti
i calcoli avremo:
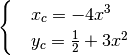
Prendiamo un software di geometria interattiva (Geogebra, DrGeo, Cabri, ecc),
disegniamo la parabola e costruiamo l’animazione che al variare
di  disegna il cerchio osculatore per mezzo delle formule che
calcolano i centri e i raggi.
disegna il cerchio osculatore per mezzo delle formule che
calcolano i centri e i raggi.
Osservazioni su alcune curvature¶
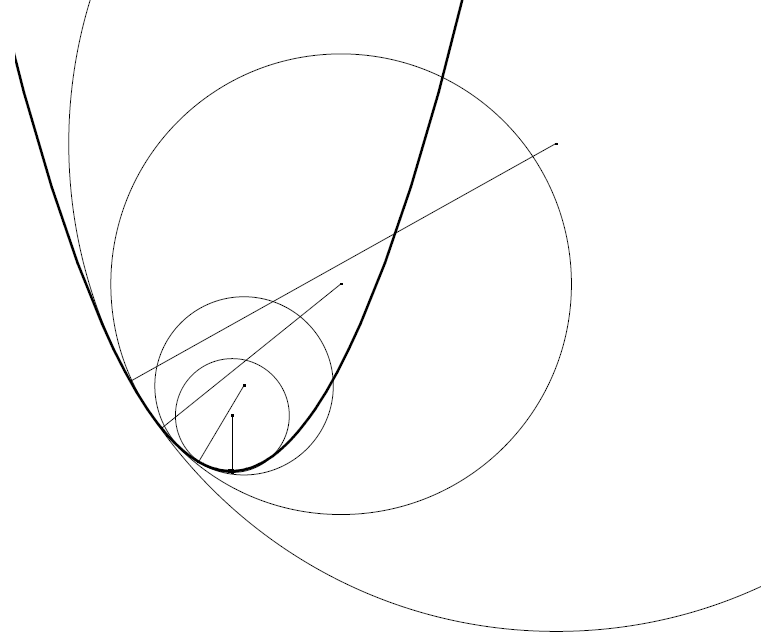
Le stesse formule, applicate alla sinusode danno luogo al disegno seguente
Il disegno mostra raggi verticali di lunghezza unitaria per 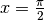 .
Infatti i calcoli ce lo confermano:
.
Infatti i calcoli ce lo confermano:
![r(x)=\frac{\left[1+f'(x)^2\right]^\frac{3}{2}}{|f^{''}(x)|}=
\frac{(1+\cos^2 x)^\frac{3}{2}}{|\sin x|}](../../../_images/math/c187398522feea6c26fbc34434d3a7a3526c94bc.png)
dove usiamo il valore assoluto per non dover dipendere dal tipo di concavità
positiva o negativa segnalata dalla derivata seconda. Per 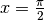 si ha
si ha
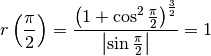
Il raggio di curvatura per la sinusoide è minimo quando vale 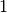 ,
in corrispondenza dei massimi e dei minimi della funzione, dove c’è il
massimo di curvatura. Si possono allora trovare i massimi di curvatura di un grafico
attraverso la ricerca del cerchio osculatore di raggio minimo.
,
in corrispondenza dei massimi e dei minimi della funzione, dove c’è il
massimo di curvatura. Si possono allora trovare i massimi di curvatura di un grafico
attraverso la ricerca del cerchio osculatore di raggio minimo.
Per esempio, relativamente al grafico del logaritmo, abbiamo:
La funzione 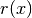 calcolata per il logaritmo è un infinito positivo
sia in
calcolata per il logaritmo è un infinito positivo
sia in  sia in
sia in  , quindi è garantita l’esistenza di
un minimo assoluto, che possiamo trovare annullando la derivata prima:
, quindi è garantita l’esistenza di
un minimo assoluto, che possiamo trovare annullando la derivata prima:
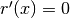 .
Svolgendo i calcoli, si trova che deve essere
.
Svolgendo i calcoli, si trova che deve essere 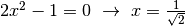 che, inserito nella formula del raggio, fornisce il valore di circa
che, inserito nella formula del raggio, fornisce il valore di circa 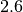 .
.
Concludiamo che il calcolo differenziale fornisce anche un metodo che consente di calcolare la curvatura dei grafici delle funzioni.
Un grafico di funzione al computer¶
Tracciando il grafico di una funzione con il computer il risultato è immediato e tutte le informazioni utili sembrano già disponibili. In realtà non tutte sono evidenti, e occorre qualche calcolo per ricavarle. Vediamo un esempio
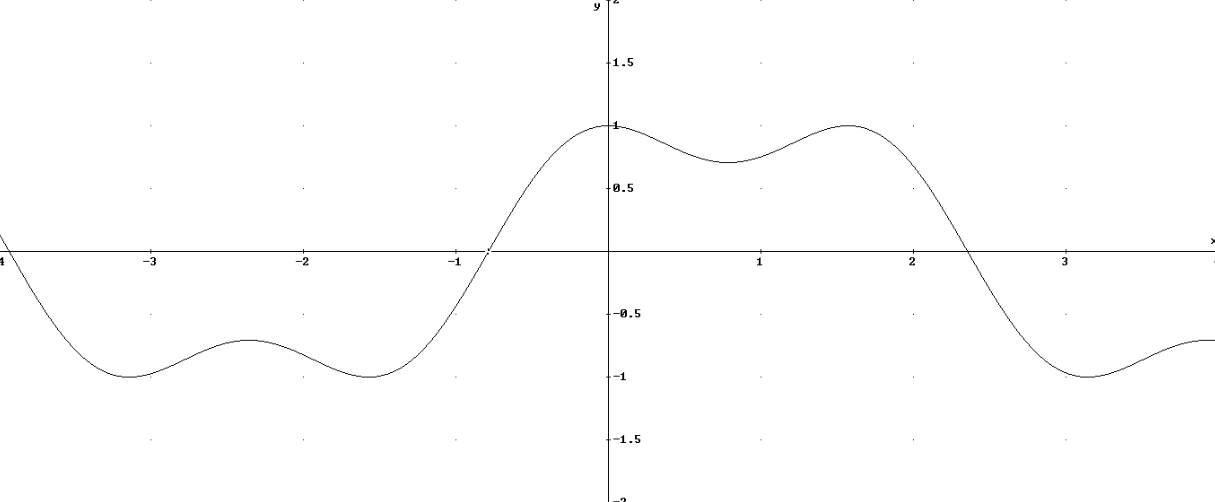
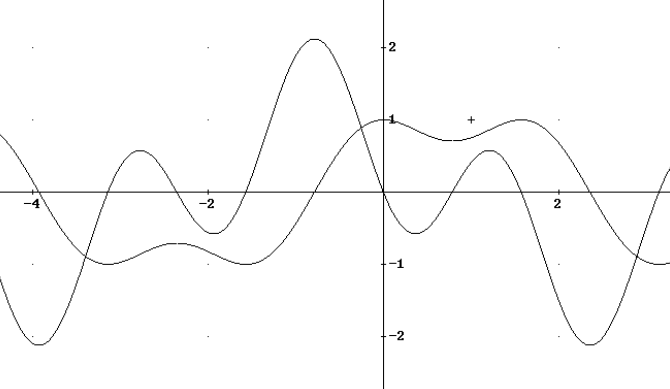
Questo è il grafico della funzione 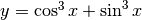 .
.
Periodicità e simmetrie¶
Alcune proprietà della funzione si cominciano a vedere dopo una variazione di scala:
Si tratta di una funzione periodica. Era un fatto intuibile, dato che la funzione è
somma di cubi di funzioni periodiche. Il periodo è 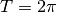 e diamo per
scontato che
e diamo per
scontato che  sia definita su tutto l’asse reale.
sia definita su tutto l’asse reale.
Note
Bisogna però osservare che la periodicità va sempre verificata: non è detto che la somma di due funzioni periodiche, con lo stesso periodo, sia una funzione periodica e, se lo è, che abbia periodo uguale a quello delle funzioni.
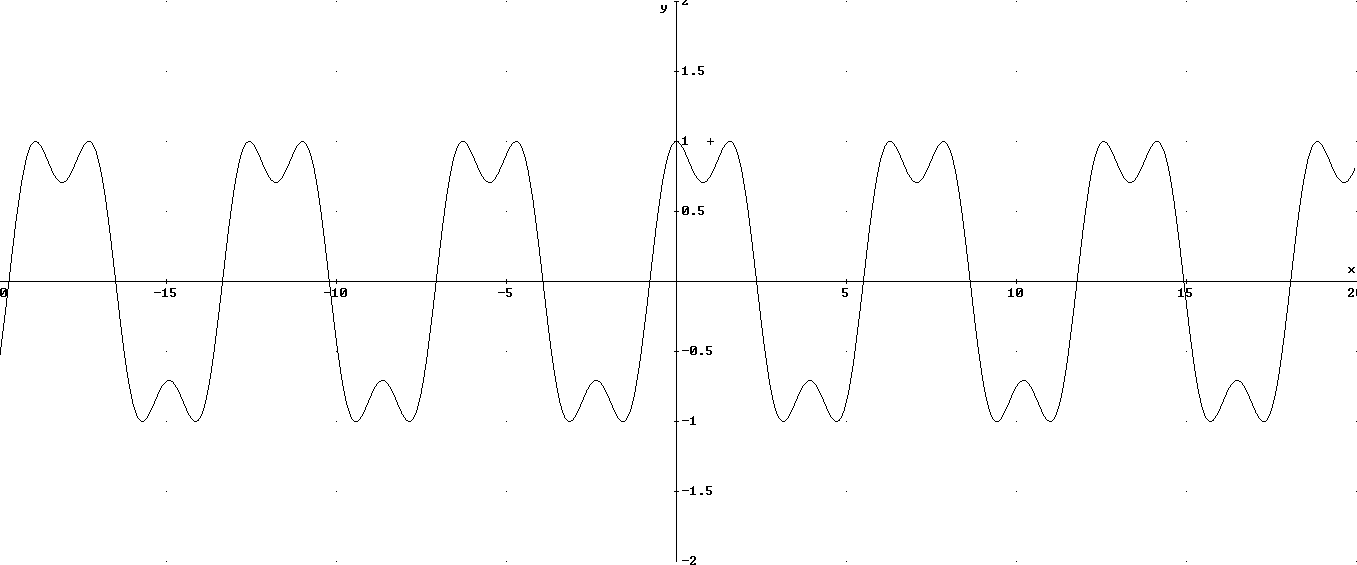
Il grafico ha altre simmetrie, oltre alle simmetrie per traslazione, secondo i
vettori multipli di ![\vec c[2\pi,0]](../../../_images/math/3fc29c42eed6dff516f671baeea8e5220858fd80.png) , dovute alla sua periodicità.
Infatti i punti di intersezione con l’asse delle ascisse sono centri per
rotazioni di
, dovute alla sua periodicità.
Infatti i punti di intersezione con l’asse delle ascisse sono centri per
rotazioni di 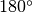 , che riportano la figura su se stessa.
Inoltre le rette verticali passanti per i minimi della parte superiore e per i
massimi di quella inferiore sono assi di simmetria per il grafico. E poi l’asse
orizzontale è asse di una glisso-simmetria fra la parte positiva e quella negativa del grafico.
, che riportano la figura su se stessa.
Inoltre le rette verticali passanti per i minimi della parte superiore e per i
massimi di quella inferiore sono assi di simmetria per il grafico. E poi l’asse
orizzontale è asse di una glisso-simmetria fra la parte positiva e quella negativa del grafico.
Intersezioni¶
Per 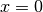 ,
, 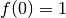 , quindi la prima intersezione con gli assi è in
, quindi la prima intersezione con gli assi è in
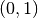 . Per le intersezioni con l’asse
. Per le intersezioni con l’asse 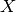 bisogna risolvere
bisogna risolvere
.
La prima intersezione con l’asse orizzontale è in 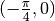 ,
le successive e le precedenti seguono il variare di
,
le successive e le precedenti seguono il variare di  . Le intersezioni
più vicine a
. Le intersezioni
più vicine a 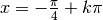 si hanno per
si hanno per 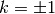 e sono
e sono
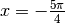 e
e 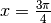 .
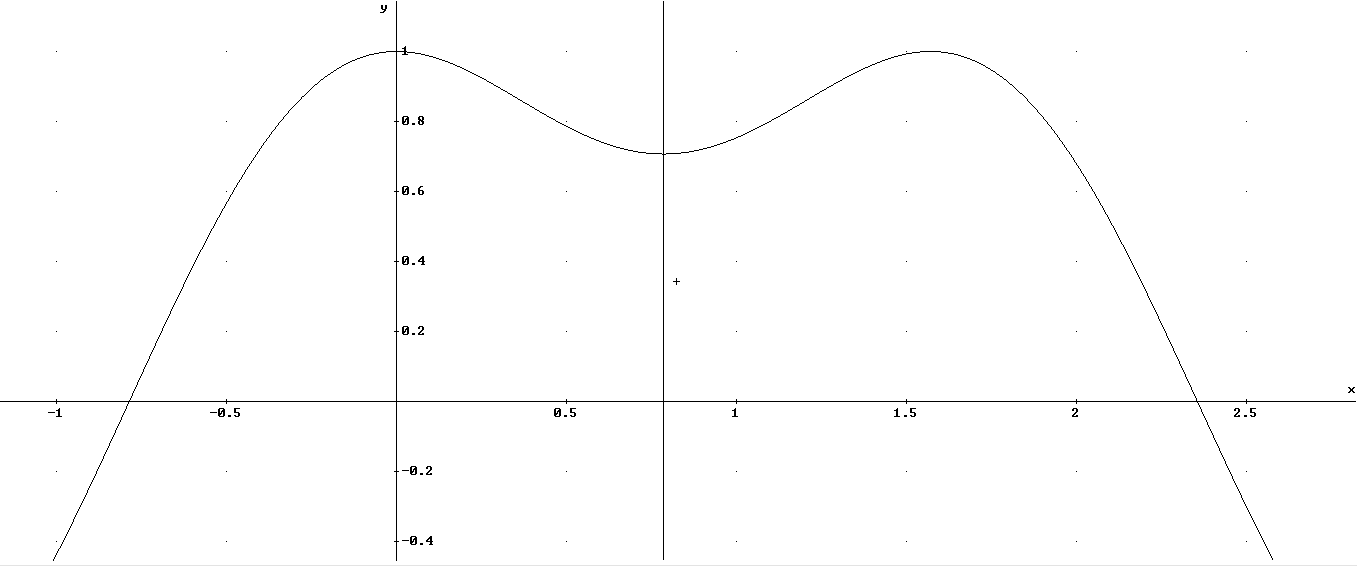
Data la simmetria centrale del grafico, basta analizzarlo nell’intervallo
.
Data la simmetria centrale del grafico, basta analizzarlo nell’intervallo
![\left[-\frac{\pi}{4},\frac{3\pi}{4}\right]](../../../_images/math/0280baa9540040ec9752d4e19537435bc833ee62.png) che rappresenta mezzo intervallo di periodicità. Poi si estenderanno le conclusioni
all’altra metà periodo.
che rappresenta mezzo intervallo di periodicità. Poi si estenderanno le conclusioni
all’altra metà periodo.
In aggiunta, si vede che gli assi verticali di simmetria
si trovano in 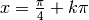 , quindi si può ancora
dimezzare l’intervallo su cui studiare la funzione, che si riduce a
, quindi si può ancora
dimezzare l’intervallo su cui studiare la funzione, che si riduce a
![\left[\frac{\pi}{4},\frac{3\pi}{4}\right]](../../../_images/math/bc932537f703d3bad4ddaa3ba73aeedb8cc21b34.png) .
.
Massimi e minimi¶
Osservando il grafico, ci aspettiamo che la derivata si annulli in
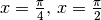 e per quest’ultimo
punto sembra ci sia un massimo assoluto.
e per quest’ultimo
punto sembra ci sia un massimo assoluto.
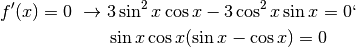
Nell’intervallo che consideriamo 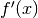 si annulla
per
si annulla
per 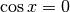 e per
e per 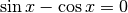 . Le soluzioni sono dunque
. Le soluzioni sono dunque
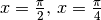 , come previsto.
I valori corrispondenti della funzione sono
, come previsto.
I valori corrispondenti della funzione sono 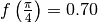 e
e
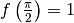 . Quest’ultimo valore poteva essere ricavato
direttamente dal grafico, sulla base della simmetria assiale della curva.
. Quest’ultimo valore poteva essere ricavato
direttamente dal grafico, sulla base della simmetria assiale della curva.
Viste le simmetrie, abbiamo che nell’intervallo
![\left[-\frac{\pi}{4},\frac{3\pi}{4}\right]](../../../_images/math/0280baa9540040ec9752d4e19537435bc833ee62.png)
 cresce da
cresce da 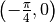 fino a
fino a 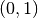 (massimo assoluto), poi decresce fino al minimo relativo nel punto
(massimo assoluto), poi decresce fino al minimo relativo nel punto
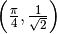 , poi cresce fino ad
un nuovo massimo assoluto in
, poi cresce fino ad
un nuovo massimo assoluto in 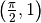 e infine
decresce.
e infine
decresce.
L’analisi può essere estesa ad un intero periodo, mediante una simmetria
centrale, di centro 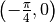 . L’intervallo diventa
allora
. L’intervallo diventa
allora ![\left[-\frac{5}{4}\pi,\frac{3}{4}\pi\right]](../../../_images/math/2e7659491cde0b429b866ea31eec683bb3b6e812.png) e nella metà
periodo che ora si aggiunge a sinistra rispetto a prima, i minimi assoluti negativi
sono i corrispondenti dei massimi positivi già calcolati e il massimo relativo
negativo è il corrispondente del minimo relativo già visto.
e nella metà
periodo che ora si aggiunge a sinistra rispetto a prima, i minimi assoluti negativi
sono i corrispondenti dei massimi positivi già calcolati e il massimo relativo
negativo è il corrispondente del minimo relativo già visto.
Analisi della derivata prima¶
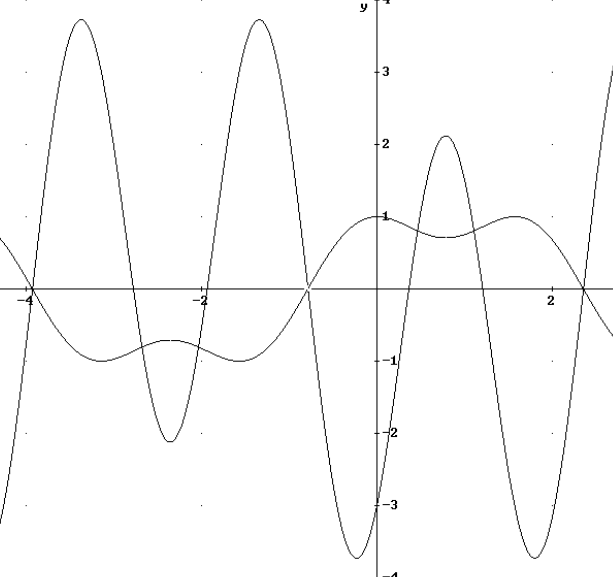
Aggiungendo al grafico della funzione anche quello di 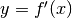 ,
vediamo che questo
,
vediamo che questo
- raggiunge i valori estremi in corripondenza delle intersezioni per cui
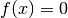 , che sono i punti di massima pendenza, in valore assoluto
, che sono i punti di massima pendenza, in valore assoluto - interseca sei volte l’asse orizzontale, in corrispondenza dei massimi e dei
minimi di
 .
.
Se 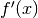 cambia segno ripetutamente vuol dire che
cambia segno ripetutamente vuol dire che  cambia
concavità e questo preannuncia la presenza di flessi.
cambia
concavità e questo preannuncia la presenza di flessi.
Analisi della derivata seconda¶
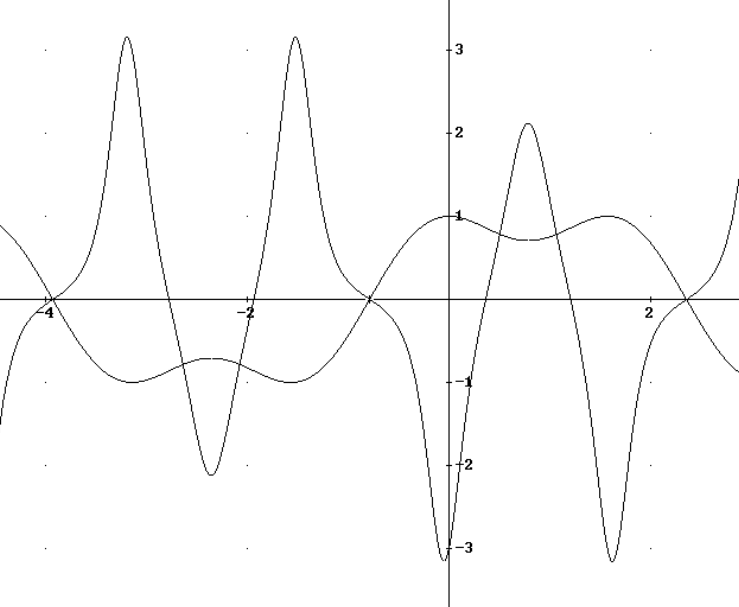
La derivata seconda è
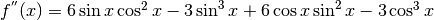 .
Cerchiamo gli zeri di questa funzione.
.
Cerchiamo gli zeri di questa funzione.
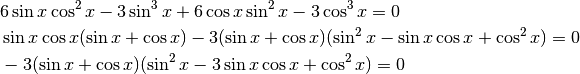
Il prodotto si azzera, nell’intervallo 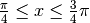 , se
, se
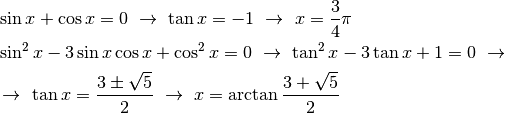
Anche la derivata seconda si azzera sei volte in un periodo, cambiando segno.
La funzione quindi cambia concavità. In un periodo ci sono due punti di flesso dove
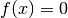 e altri quattro, a due a due simmetrici rispetto al minimo
positivo e al massimo negativo.
e altri quattro, a due a due simmetrici rispetto al minimo
positivo e al massimo negativo.
Curvatura¶
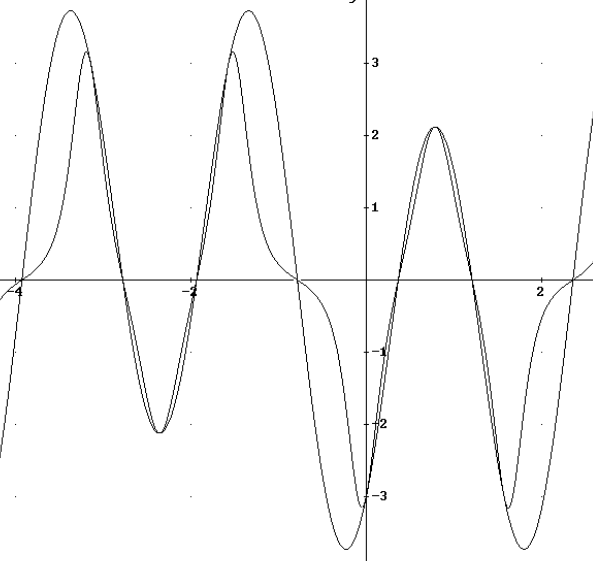
L’espressione della curvatura
![k(x)=\frac{f^{''}(x)}{\left[1+f'(x)\right]^\frac{3}{2}}](../../../_images/math/04fb8fabfbf29c38e6818a4e06a811f5f285f214.png) è così complicata che è meglio che sia Derive a calcolarla.
è così complicata che è meglio che sia Derive a calcolarla.
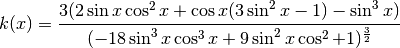
Chiediamo direttamente al software di tracciare il grafico della curvatura insieme a quello della funzione.
Gli zeri dell’espressione della curvatura sono gli stessi della derivata seconda, sono i punti a curvatura nulla, cioè i tratti rettilinei del grafico della funzione e corrispondono ai punti di flesso. La curvatura è massima, in valore assoluto, nei punti di massimo e di minimo della funzione, dove il raggio del cerchio osculatore è minimo.
Note
Perché diciamo che nei punti di flesso il grafico ha un tratto
rettilineo? Tutto dipende dai punti di contatto fra il grafico e la tangente.
In genere la tangente in un punto  al grafico della funzione si
distanzia ben presto dalla funzione: nei punti
al grafico della funzione si
distanzia ben presto dalla funzione: nei punti 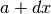 le differenze
fra i valori della tangente e quelli della funzione sono infinitesimi di ordine
superiore a
le differenze
fra i valori della tangente e quelli della funzione sono infinitesimi di ordine
superiore a 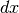 , in genere dell’ordine di
, in genere dell’ordine di 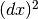 .
Nei punti di flesso, però, queste differenze sono dell’ordine di
.
Nei punti di flesso, però, queste differenze sono dell’ordine di 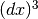 ,
quindi il contatto è molto più alto perché nella monade di
,
quindi il contatto è molto più alto perché nella monade di  nemmeno
un microscopio che vede gli infinitesimi dell’ordine di
nemmeno
un microscopio che vede gli infinitesimi dell’ordine di 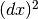 riesce distinguere queste distanze.
riesce distinguere queste distanze.
Confrontiamo il grafico della derivata seconda con quello della curvatura.
I due grafici si distinguono: i punti di massima curvatura non sono quelli in cui è massima la derivata seconda. Infatti la derivata seconda dà una misura della concavità, non della curvatura.
Riassunto¶
- Le funzioni iperreali hanno per dominio intervalli di numeri che sono estensione di intervalli reali. Gli intervalli estesi contengono numeri standard e non standard (infiniti, infinitesimi) e mantengono le stesse proprietà date per gli intervalli reali.
- Rispetto al dominio, un punto può essere interno, esterno o di frontiera. Si dice interno all’estensione di un intervallo, il punto la cui monade vi è inclusa. Si dice di frontiera il punto nella cui monade vi sono sia punti interni che punti esterni.
- Si dice isolato il punto di frontiera per il quale l’intersezione fra la sua monade e l’intervallo è data solo dal punto stesso. Se invece oltre al punto, nell’intersezione cadono altri punti della monade, allora il punto si dice di accumulazione.
- Il procedimento che porta a disegnare manualmente nel modo più preciso il grafico di una funzione, si chiama studio di funzione. Consiste dei seguenti passi: 1. Definizione del dominio; 2. Analisi delle simmetrie; 3. Calcolo delle intersezioni con gli assi; 3. Studio del segno delle funzione; 5. Studio del comportamento asintotico. 6. Studio dell’andamento e ricerca dei massimi e dei minimi; 7. Analisi delle concavità e ricerca dei punti di flesso.
- Per completare le informazioni precedenti è possibile approfondire il lavoro con l’analisi delle curvature del grafico. Attraverso opportuni calcoli è anche possibile calcolare il raggio e il centro del cerchio osculatore ad un punto qualsiasi del grafico.
- I software dedicati sono utili e potenti strumenti per il tracciamento dei grafici. Non sempre consentono di definire con precisione i punti notevoli e quindi spesso il loro lavoro deve essere integrato con gli strumenti del calcolo differenziale.
Esercizi¶
- Definisci il punto
 come punto di accumulazione sinistro nei tre casi
in cui questa definizione ha senso.
come punto di accumulazione sinistro nei tre casi
in cui questa definizione ha senso. - Ripercorri tutte le fasi dell’esercizio guida, esplicitando anche i calcoli sottintesi.
- Applica le formule per il calcolo della curvatura al grafico della sinusoide, di cui puoi osservare il disegno nel testo.
- Svolgi i calcoli indicati dal testo per trovare il raggio di massima curvatura della funzione logaritmo e applica al caso del logaritmo le formule per trovare le coordinate del centro.
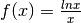

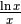

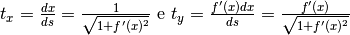
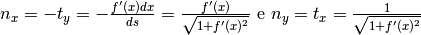

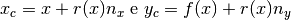
![y=\ln x\mbox{ , }f'(x)=\frac{1}{x} \mbox{ , }f^{''}(x)=-\frac{1}{x^2}\\
r(x)=\frac{\left[1+f'(x)^2\right]^\frac{3}{2}}{|f^{''}(x)|}=
\frac{\left(1+\frac{1}{x^2}\right)^\frac{3}{2}}{\left|-\frac{1}{x^2}\right|}=
\frac{(x^2+1)^\frac{3}{2}}{x}](../../../_images/math/52e4819c9a3516b90c474d3c14a1f0acb3a77b7f.png)