La risoluzione numerica delle equazioni¶
Sappiamo risolvere alcuni tipi di equazioni: quelle algebriche di 1° e 2° grado e alcune equazioni fondamentali trascendenti: con funzioni circolari, esponenziali, logaritmiche. Sappiamo anche che per molte equazioni non esiste una formula risolutiva, come avviene per le equazioni di 2° grado. In questo capitolo impareremo alcune tecniche che consentono di affrontare con successo equazioni di ogni tipo, che altrimenti sarebbero non risolvibili.
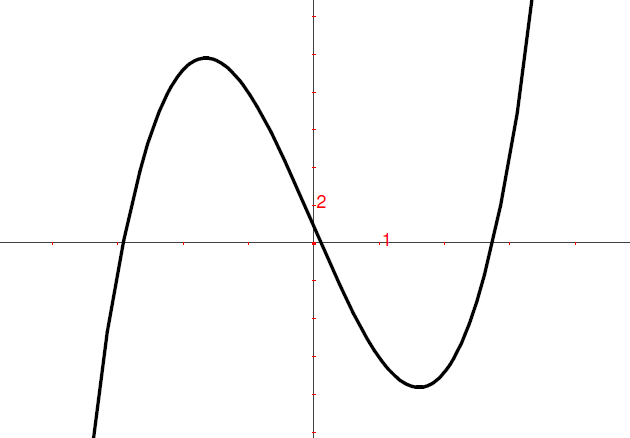
Iniziamo da un’equazione algebrica di 3° grado: 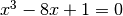 .
Sappiamo che può avere al massimo tre soluzioni.
Ma siamo sicuri che esista una soluzione?
Su questo possiamo essere sicuri.
Consideriamo infatti la funzione
.
Sappiamo che può avere al massimo tre soluzioni.
Ma siamo sicuri che esista una soluzione?
Su questo possiamo essere sicuri.
Consideriamo infatti la funzione 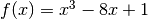 .
Risolvere l’equazione significa cercare gli zeri della funzione e possiamo
affermare con certezza che almeno uno zero esiste perché la funzione è
continua, è asintoticamente indistinguibile da
.
Risolvere l’equazione significa cercare gli zeri della funzione e possiamo
affermare con certezza che almeno uno zero esiste perché la funzione è
continua, è asintoticamente indistinguibile da 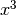 e, essendo negativa
per
e, essendo negativa
per  infinito negativo e positiva per
infinito negativo e positiva per  infinito positivo,
non può che annullarsi per almeno un valore di
infinito positivo,
non può che annullarsi per almeno un valore di  .
.
Il primo modo per risolvere è quello tutto tecnologico. Visualizzando il
grafico della funzione si vede che ci sono tre intersezioni con l’asse
 .
Basta allora ingrandire opportunamente la scala orizzontale e si trovano
approssimativamente le soluzioni: una soluzione pari a circa
.
Basta allora ingrandire opportunamente la scala orizzontale e si trovano
approssimativamente le soluzioni: una soluzione pari a circa 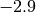 ,
un’altra è circa
,
un’altra è circa 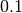 e l’ultima circa
e l’ultima circa 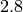 .
Anche le calcolatrici moderne danno un valido aiuto,
basta immettere, oltre alla funzione, anche l’intervallo entro il quale ci si
aspetta la soluzione: per esempio la soluzione compresa fra 2 e 3, calcolata
in questo modo, fornisce il valore
.
Anche le calcolatrici moderne danno un valido aiuto,
basta immettere, oltre alla funzione, anche l’intervallo entro il quale ci si
aspetta la soluzione: per esempio la soluzione compresa fra 2 e 3, calcolata
in questo modo, fornisce il valore 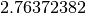 .
.
Questo sistema, comodo e efficace, non è sempre usabile. Pur ammettendo l’uso della calcolatrice, abbiamo comunque bisogno di stimare quali siano gli intervalli all’interno dei quali cercare le soluzioni e non è detto che, una volta tracciato il grafico, ci sia facile osservare il piano nei punti giusti e al giusto ingrandimento.
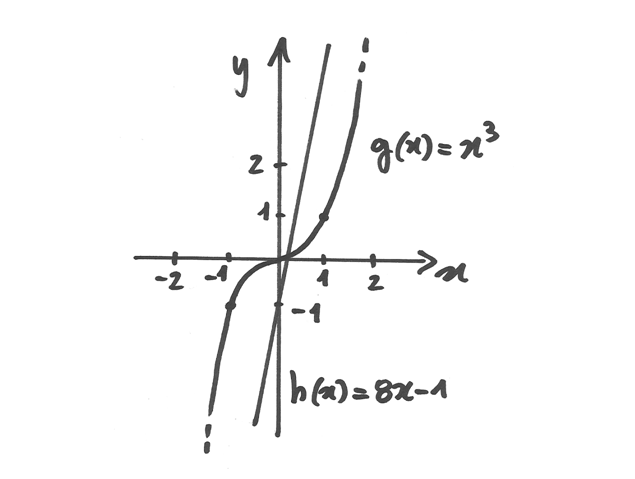
Se si opera solo con carta e matita, una prima ricerca degli intervalli che
contengono una soluzione si può fare spezzando la funzione in due:
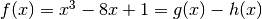 , con
, con 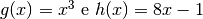 .
In questo modo
.
In questo modo 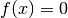 diventa
diventa 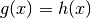 , cioé
, cioé 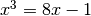 .
Scritta così, l’equazione chiede di cercare i valori di
.
Scritta così, l’equazione chiede di cercare i valori di  per
i quali le due funzioni
per
i quali le due funzioni 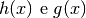 sono uguali.
I grafici delle due funzioni possono essere tracciati anche a mano
sono uguali.
I grafici delle due funzioni possono essere tracciati anche a mano
Si vede bene che fra 0 e 1 c’è un’intersezione e poi si intuisce che ne esistono altre due perché la cubica si impenna più rapidamente della retta. A mano si costruisce una tabella per verificare in quali intervalli i valori di una funzione scavalchino l’altra.
| x | h(x) | g(x) |
|---|---|---|
| 2 | 8 | 15 |
| 3 | 27 | 23 |
| -2 | -8 | -17 |
| -3 | -27 | -25 |
Poiché negli intervalli fra 2 e 3 e fra -2 e -3 i valori di una funzione
superano i valori dell’altra, sicuramente in questi intervalli vi sarà almeno
un valore di  che rende le due funzioni uguali.
che rende le due funzioni uguali.
Note
In un caso semplice come questo, si può anche evitare di spezzare
 in due funzioni. La tabella allora serve a evidenziare in quali
intervalli la funzione cambia i suoi valori, da positivi a negativi o
viceversa.
in due funzioni. La tabella allora serve a evidenziare in quali
intervalli la funzione cambia i suoi valori, da positivi a negativi o
viceversa.
Il metodo dicotomico¶
A questo punto cerchiamo di migliorare la precisione, cioè individuiamo
intervalli più stretti nei quali cercare le soluzioni. Un modo facile è spezzare
in due gli intervalli precedenti: per esempio invece di ![[2,3]](../../../_images/math/f2228186c583f7b81dd1f3355dd7b1f20058efa5.png) utilizziamo
utilizziamo ![[2,2.5]](../../../_images/math/b248f3c309ebc11685c921fd6262ff0abd2f9b9d.png) e
e ![[2.5,3]](../../../_images/math/7592762fb086bc1cd0f76d8c65271325e6c70745.png) . Con una tabella simile alla
precedente possiamo verificare che la soluzione è contenuta nel secondo dei due
intervalli. Allora agiremo (con la calcolatrice) su
. Con una tabella simile alla
precedente possiamo verificare che la soluzione è contenuta nel secondo dei due
intervalli. Allora agiremo (con la calcolatrice) su ![[2.5,3]](../../../_images/math/7592762fb086bc1cd0f76d8c65271325e6c70745.png) allo stesso
modo, cioè dividendolo per il suo punto medio e verificando i risultati con la
tabella. Ogni volta la precisione aumenterà e potremo ripetere il procedimento
a piacere, fermandoci quando avremo raggiunto il grado di precisione desiderato,
cioè quando l’ampiezza dell’ultimo intervallo sarà minore dell’errore
prefissato.
allo stesso
modo, cioè dividendolo per il suo punto medio e verificando i risultati con la
tabella. Ogni volta la precisione aumenterà e potremo ripetere il procedimento
a piacere, fermandoci quando avremo raggiunto il grado di precisione desiderato,
cioè quando l’ampiezza dell’ultimo intervallo sarà minore dell’errore
prefissato.
Tutta questa serie di operazioni sempre uguali definisce l’algoritmo dicotomico, così detto perché gli intervalli vengono ogni volta spezzati in due. L’algoritmo si può anche descrivere con un linguaggio di programmazione:
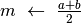
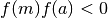


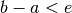
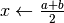
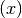
Nel listato si prevede che la funzione sia già data. Il controllo sulla
differenza di segno agli estremi dell’intervallo avviene moltiplicando i valori
(quinta riga).  è l’errore massimo consentito.
è l’errore massimo consentito.
L’algoritmo dicotomico restringe
progressivamente l’intervallo in cui si trova la soluzione.
Fissato il massimo errore accettabile, possiamo restringere l’intervallo fino
a farlo diventare più piccolo di questo errore.
Se ripetiamo infinite volte l’algoritmo, gli estremi arriveranno ad appartenere
alla sua monade dello zero della funzione e quindi la parte standard di un
estremo è lo zero della funzione.
Modificando leggermente il programma possiamo stampare i valori degli estremi
dell’intervallo e osservare così come quest’ultimo si restringe attorno
ad un valore che possiamo considerare lo zero della funzione a meno di un
errore prefissato.
Ricordiamo che la funzione era
definita a parte e l’errore massimo previsto era 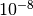 .
.
| k | 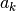 |
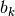 |
|---|---|---|
| 0 | 2 | 3 |
| 1 | 2.5 | 3 |
| 2 | 2.75 | 3 |
| 3 | 2.75 | 2.875 |
| 4 | 2.75 | 2.78125 |
| 5 | 2.75 | 2.765625 |
| 6 | 2.75 | 2.765625 |
| 7 | 2.7578125 | 2.765625 |
| 8 | 2.76171875 | 2.765625 |
| 9 | 2.76367187 | 2.765625 |
| 10 | 2.76367187 | 2.76464884 |
| ... | ... | ... |
| 25 | 2.76372379 | 2.76372382 |
| 26 | 2.76372381 | 2.76372382 |
| 27 | 2.76372382 | 2.76372382 |
Come si vede, in 27 cicli, l’algoritmo ha racchiuso la soluzione in un intervallo i cui estremi sono passati dal differire di una unità al differire meno di un centomilionesimo.
È possibile stabilire a priori quante iterazioni occorre fare per ridurre l’intervallo a un’ampiezza minore dell’errore  prefissato, infatti
ad ogni passo l’intervallo viene dimezzato e quindi, dopo
prefissato, infatti
ad ogni passo l’intervallo viene dimezzato e quindi, dopo 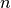 iterazioni, l’ampiezza è diventata:
iterazioni, l’ampiezza è diventata: 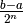 .
Si tratta allora di determinare il più piccolo valore di
.
Si tratta allora di determinare il più piccolo valore di 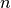 per cui
per cui
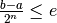 . Risolvendo la disequazione abbiamo:
. Risolvendo la disequazione abbiamo:
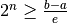 e
e 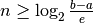
Applicando la formula al caso dell’equazione cubica che abbiamo appena risolto otteniamo
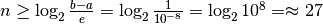
Per riassumere la sequenza delle operazioni:
1. Si separano le soluzioni, cioè si definisce per ogni soluzione un intervallo
che la contenga. Questo si fa per via grafica, cercando le intersezioni
del grafico con l’asse  . Spesso è comodo riscrivere la funzione
come uguaglianza fra due altre funzioni e cercare i punti di ascissa che
corrispondono alle intersezioni fra i loro due grafici.
. Spesso è comodo riscrivere la funzione
come uguaglianza fra due altre funzioni e cercare i punti di ascissa che
corrispondono alle intersezioni fra i loro due grafici.
2. Individuati gli intervalli, si applica l’algoritmo dicotomico, controllando
che agli estremi dell’intervallo  abbia segno diverso,
oppure che
abbia segno diverso,
oppure che 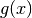 e
e 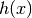 nell’intervallo “si scavalchino”.
nell’intervallo “si scavalchino”.
Tutto ciò si basa su due premesse: la funzione deve essere continua e deve assumere valori di segno opposto agli estremi di ogni intervallo. Lo precisiamo nel prossimo teorema.
Teorema degli zeri di una funzione continua¶
Il procedimento del metodo dicotomico può essere esteso infinitamente, individuando intervalli sempre più piccoli. In questo modo si giunge a dimostrare un’importante proprietà delle funzioni continue.
Se ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) , con
, con 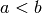 , è l’intervallo da suddividere, le divisioni
successive generano due successioni di estremi
, è l’intervallo da suddividere, le divisioni
successive generano due successioni di estremi
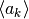 e
e 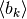 , la prima non decrescente e la
seconda non crescente. L’ampiezza del k_esimo intervallo sarà
, la prima non decrescente e la
seconda non crescente. L’ampiezza del k_esimo intervallo sarà
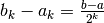 . Le due successioni sono monotone e limitate,
quindi convergenti, e all’infinito vale
. Le due successioni sono monotone e limitate,
quindi convergenti, e all’infinito vale
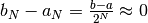 ,
cioè la differenza fra i due termini diventa infinitesima e quindi essi
appartengono alla stessa monade e individuano lo stesso numero standard che
chiameremo
,
cioè la differenza fra i due termini diventa infinitesima e quindi essi
appartengono alla stessa monade e individuano lo stesso numero standard che
chiameremo 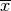 .
.
Immaginiamo 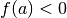 e
e 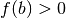 (ma il ragionamento non cambia nel
caso contrario); grazie al nostro algoritmo avremo per ogni
(ma il ragionamento non cambia nel
caso contrario); grazie al nostro algoritmo avremo per ogni  :
:
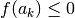 e
e 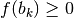 , che vale ovviamente anche con indici
infiniti.
Quindi
, che vale ovviamente anche con indici
infiniti.
Quindi 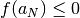 e
e 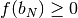 . Ma abbiamo visto che
. Ma abbiamo visto che
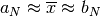 . Qui entra in gioco la continuità
della funzione, per cui
. Qui entra in gioco la continuità
della funzione, per cui
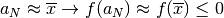 e
e
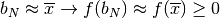 .
Non potendo essere contemporaneamente maggiore e minore di zero,
.
Non potendo essere contemporaneamente maggiore e minore di zero,
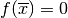 .
.
Il Teorema degli zeri quindi assicura che
una funzione continua nell’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) ,
che assume valori di segno diverso agli estremi, ha certamente
almeno uno zero in un punto interno all’intervallo.
,
che assume valori di segno diverso agli estremi, ha certamente
almeno uno zero in un punto interno all’intervallo.
Note
Si potrebbe dare una dimostrazione analoga anche nel caso che
 venga spezzata in due funzioni
venga spezzata in due funzioni 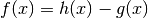 ,
ma preferiamo cogliere l’occasione per approfondire il discorso sulle
funzioni continue e pervenire in modo diverso allo stesso risultato.
,
ma preferiamo cogliere l’occasione per approfondire il discorso sulle
funzioni continue e pervenire in modo diverso allo stesso risultato.
Proprietà delle funzioni continue¶
Se due funzioni 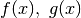 sono continue nel punto
sono continue nel punto  , allora
è continua in
, allora
è continua in  anche la loro somma, la loro differenza, il loro
prodotto e il loro quoziente, purché esista in
anche la loro somma, la loro differenza, il loro
prodotto e il loro quoziente, purché esista in  .
Quindi vale:
.
Quindi vale:
Se per 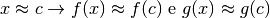 ,
allora sempre per
,
allora sempre per 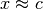
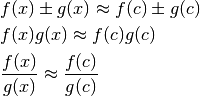
Queste proprietà sono intuitive e discendono direttamente dalle proprietà della
parte standard di un iperreale. Infatti 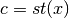 perché è standard e
perché è standard e
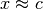 .
. 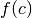 è standard e
è standard e 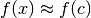 , allora
, allora
![f(c)=st[f(x)]](../../../_images/math/bc9da20103f7774762c8c86a7a6f2a510643bb5a.png) .
.
La continuità in  si può anche esprimere dicendo che
si può anche esprimere dicendo che
![f[st(x)]=st[f(x)]](../../../_images/math/9dfe2ac6a2a94dbab45b6acca935ac91c7dc4c4a.png) .
.
In riferimento alla nota precedente, la continuità della differenza
consente di dimostrare il Teorema degli zeri anche nella versione in cui
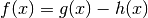 .
.
Il metodo delle tangenti¶
Nel suddividere l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) alla ricerca dello zero della
funzione, il metodo delle tangenti è più efficiente del metodo dicotomico, cioè
raggiunge l’obiettivo più rapidamente.
L’idea è di sostituire al grafico della funzione la sua tangente in un punto
alla ricerca dello zero della
funzione, il metodo delle tangenti è più efficiente del metodo dicotomico, cioè
raggiunge l’obiettivo più rapidamente.
L’idea è di sostituire al grafico della funzione la sua tangente in un punto
 vicino alla soluzione
vicino alla soluzione 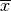 . L’intersezione della
tangente con l’asse
. L’intersezione della
tangente con l’asse  determina il valore
determina il valore 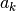 , oppure
, oppure
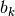 , che restringe l’intervallo
, che restringe l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) attorno a
attorno a
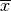 .
.
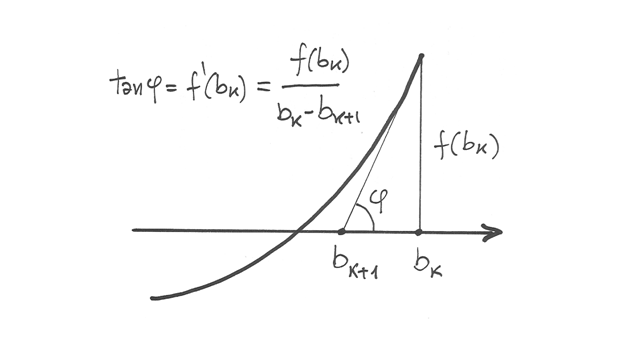
L’equazione della tangente in  è data dal Polinomio di Taylor del primo
ordine, sviluppato per
è data dal Polinomio di Taylor del primo
ordine, sviluppato per 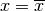 :
:
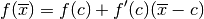
Poiché
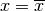 è lo zero della funzione,
è lo zero della funzione, 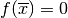 quindi si ricava il valore (approssimato al primo ordine)
quindi si ricava il valore (approssimato al primo ordine)
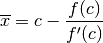
Come si vede da questo primo disegno, non è detto che la posizione di  garantisca che la tangente intersechi l’asse orizzontale in modo da restringere
l’intervallo
garantisca che la tangente intersechi l’asse orizzontale in modo da restringere
l’intervallo ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) . Perché questo avvenga occorre controllare che il
grafico della funzione in tutto
. Perché questo avvenga occorre controllare che il
grafico della funzione in tutto ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) abbia la stessa concavità.
Esaminiamo i quattro casi possibili:
abbia la stessa concavità.
Esaminiamo i quattro casi possibili:
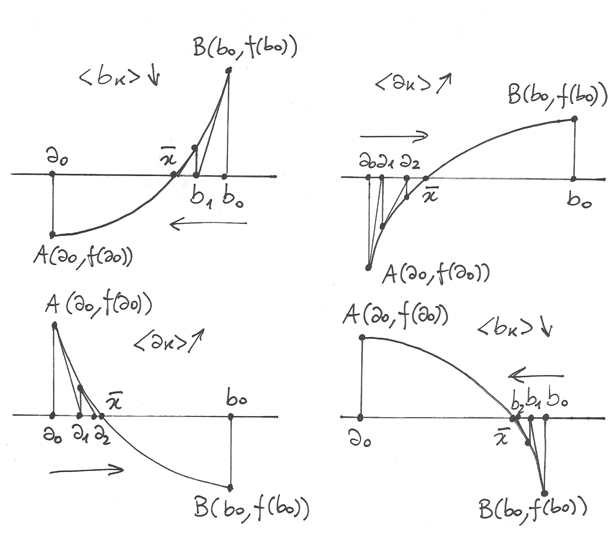
L’intervallo attorno a 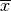 si restringe se le tangenti
successive partono da un grafico con la concavità dello stesso tipo.
si restringe se le tangenti
successive partono da un grafico con la concavità dello stesso tipo.
Questi quattro grafici appartengono a funzioni che hanno
- valori di segno diverso agli estremi dell’intervallo
- monotone
- concave sempre verso l’alto o sempre verso il basso.
La prima condizione è necessaria perché esista almeno una soluzione
(Teorema degli zeri),
la seconda perché la soluzione sia unica (stiamo cercando di separare le
soluzioni e ci occupiamo solo di ![[a,b]](../../../_images/math/12af35e3c5b91cb10e80da1234085a4387f8d98a.png) ),
la terza perché le tangenti successive restringano l’intervallo approssimando
la soluzione.
),
la terza perché le tangenti successive restringano l’intervallo approssimando
la soluzione.
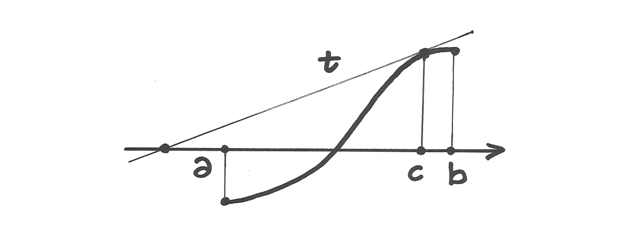
Ragioniamo sul primo disegno in fig.16.5, come esempio: la prima tangente è
tracciata in 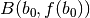 e, a causa della concavità, intercetta
l’asse delle ascisse in un punto
e, a causa della concavità, intercetta
l’asse delle ascisse in un punto 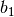 più vicino alla soluzione, e così
avverrà con le tangenti successive, che restringeranno l’intervallo unicamente
da destra.
più vicino alla soluzione, e così
avverrà con le tangenti successive, che restringeranno l’intervallo unicamente
da destra.
Iterando il procedimento, si definisce una successione
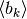 decrescente, con
decrescente, con
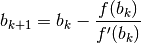
È una successione monotona e limitata, che converge a un numero
standard  . Per le proprietà viste sulle funzioni continue, se prendiamo
le parti standard, abbiamo
. Per le proprietà viste sulle funzioni continue, se prendiamo
le parti standard, abbiamo
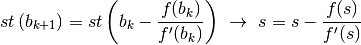
da cui 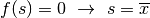 .
.
Gli altri casi della figura 16.5 si trattano in modo analogo, perché le formule
date per 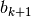 valgono anche per
valgono anche per 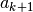 . Ma come scegliere
quale fomula sviluppare, cioé le tangenti vanno tracciate a partire da
. Ma come scegliere
quale fomula sviluppare, cioé le tangenti vanno tracciate a partire da  o da
o da 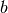 ? Se la concavità è rivolta verso l’alto sceglieremo l’estremo con
ordinata positiva, altrimenti quello con ordinata negativa.
? Se la concavità è rivolta verso l’alto sceglieremo l’estremo con
ordinata positiva, altrimenti quello con ordinata negativa.
E come faremo a controllare dove si rivolge la concavità? Qui interviene una regola che svilupperemo più avanti: se la derivata seconda è positiva nell’intervallo dato, allora la concavità è rivolta verso l’alto, altrimenti è rivolta verso il basso.
Dunque i controlli preliminari da effettuare prima di applicare il metodo delle tangenti sono:
- Il segno agli estremi dell’intervallo: deve essere diverso.
- La monotonia:
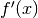 costantemente positiva o negativa.
costantemente positiva o negativa. - La concavità:
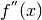 costantemente positiva o negativa.
costantemente positiva o negativa. - La scelta dell’estremo a cui applicare l’algoritmo, in base ai punti 1. e 3.
Un esempio¶
Applichiamo il metodo delle tangenti alla funzione già usata nel paragrafo del
metodo dicotomico: 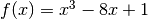 , anche qui per cercare la soluzione
nell’intervallo
, anche qui per cercare la soluzione
nell’intervallo ![[2,3]](../../../_images/math/f2228186c583f7b81dd1f3355dd7b1f20058efa5.png) .
.
 agli estremi:
agli estremi: 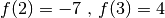
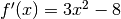 , positiva nell’intervallo: la funzione è crescente.
, positiva nell’intervallo: la funzione è crescente.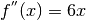 , positiva nell’intervallo: concavità verso l’alto.
, positiva nell’intervallo: concavità verso l’alto.- Le tangenti si tracciano a partire da
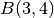 .
.
Anche in questo caso, per accelerare il calcolo usiamo un algoritmo:
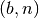 ;
;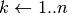 esegui
esegui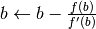 ;
;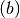 ;
;Supponiamo che i controlli siano fatti, 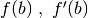 siano date
e lanciamo il programma con 5 iterazioni. Ecco l’output
siano date
e lanciamo il programma con 5 iterazioni. Ecco l’output
| k | 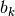 |
|---|---|
| 0 | 3 |
| 1 | 2.78947368 |
| 2 | 2.76408434 |
| 3 | 2.76372389 |
| 4 | 2.76372382 |
| 5 | 2.76372382 |
Già con quattro interazioni si perviene alla soluzione con la stessa precisione raggiunta in 27 iterazioni col metodo dicotomico.
Il metodo delle contrazioni¶
Nei metodi precedenti, la soluzione viene ricavata partendo da alcune considerazioni geometriche relative alla forma del grafico.
Ma un altro metodo permette di trovare la soluzione di un’equazione
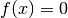 in modo automatico, senza dover fare considerazioni geometriche.
Cioè data una equazione
in modo automatico, senza dover fare considerazioni geometriche.
Cioè data una equazione 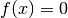 è possibile trovare una funzione
è possibile trovare una funzione
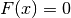 e un valore iniziale
e un valore iniziale 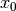 tali che la successione
definita da
tali che la successione
definita da 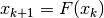 converga alla soluzione
converga alla soluzione
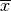 La soluzione dell’equazione sarà il numero
La soluzione dell’equazione sarà il numero
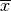 con
con 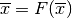 .
.
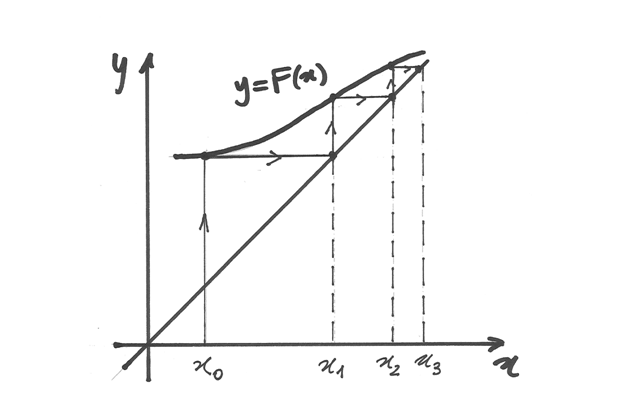
Partiamo dal significato geometrico dell’iterazione della funzione
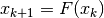 : partendo dal valore
: partendo dal valore 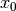 calcoliamo
calcoliamo
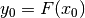 , usando la retta
, usando la retta  e a questo punto iteriamo il procedimento.
e a questo punto iteriamo il procedimento.
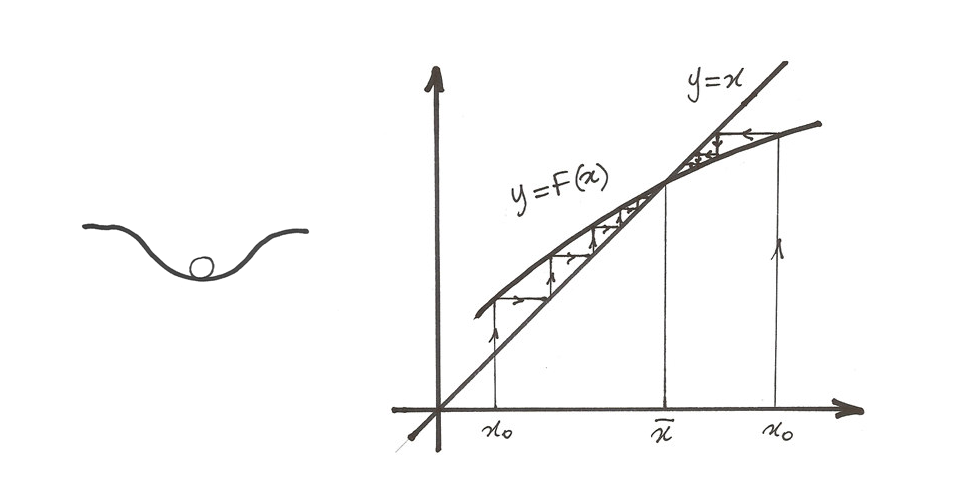
Se partissimo dal punto 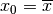 iterando il procedimento
otterremmo sempre lo stesso valore. Questo valore si chiama punto di equilibrio
della funzione
iterando il procedimento
otterremmo sempre lo stesso valore. Questo valore si chiama punto di equilibrio
della funzione 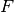 . Questo nome è dovuto ad una analogia con gli oggetti
che possono essere in equilibrio stabile o instabile. Se il punto di equilibrio
è stabile, partendo da un punto leggermente diverso da
. Questo nome è dovuto ad una analogia con gli oggetti
che possono essere in equilibrio stabile o instabile. Se il punto di equilibrio
è stabile, partendo da un punto leggermente diverso da 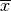 la successione tenderà a convergere a
la successione tenderà a convergere a 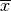
mentre se il punto di equilibrio è instabile, partendo da un punto
leggermente diverso da 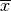 , la successione tenderà a
divergere.
, la successione tenderà a
divergere.
Riassunto¶
Esercizi¶
#. Applica il metodo delle tangenti per calcolare la radice quadrata di un
numero cercando lo zero positivo della funzione 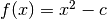 .
#. Applica il metodo delle tangenti per calcolare la radice cubica di un
numero.
.
#. Applica il metodo delle tangenti per calcolare la radice cubica di un
numero.
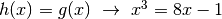
=0.png)
=0_g(x)=h(x).png)