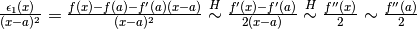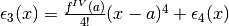I Polinomi di Taylor¶
Nello studio del comportamento asintotico di una funzione a volte siamo in difficoltà a risolvere le forme indeterminate. Abbiamo visto che la regola di de l’Hôpital ci può aiutare in alcune di queste difficoltà, molto poco in altre. Presentiamo quindi uno strumento più potente, di utilità generale.
L’idea di base del polinomio di Taylor è di approssimare il valore di una funzione come se si dovesse misurarlo secondo una scala di infinitesimi. Nella vita quotidiana quando misuriamo un oggetto, per ottenere una misura esatta ricorriamo a unità di misura sempre più fini. Per esempio per l’altezza di una finestra usiamo il metro e otteniamo un primo valore approssimato. Poi affiniamo la misura aggiungendo un certo numero di decimetri e con questo ci avviciniamo maggiormente al valore esatto, poi contiamo i centimetri e potremmo proseguire con unità sempre più fini. Lo stesso avviene in altre situazioni concrete: pesare un casco di banane con la bilancia da cucina, dosare attentamente la quantità d’acqua per l’impasto di una torta, ecc. Per “misurare” il valore di una funzione le unità di misura sempre più fini sono i vari ordini di infinitesimi.
Un esempio¶
Riprendiamo un esercizio del Cap.13: studiare il comportamento asintotico nello
zero della funzione 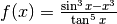 .
.
Cerchiamo una scala di infinitesimi semplice e adatta al confronto. Ricordiamo a questo proposito che due grandezze si confrontano mettendole in rapporto e se il rapporto è asintoticamente una forma di indecisione possiamo valerci della regola di de l’Hôpital.
Per il denominatore, confrontiamo il valore infinitesimo della tangente con quello dell’angolo:
.
Quindi 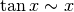 e di conseguenza
e di conseguenza 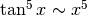 .
.
Per il numeratore, sappiamo già che 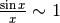 . Quindi
. Quindi 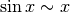 , da cui
, da cui 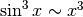 .
Ora però abbiamo un problema perché
.
Ora però abbiamo un problema perché 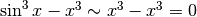 e questo
non è possibile perché lo zero è escluso dalle questioni di indistinguibilità.
In pratica ai fini del nostro esercizio, se ci limitiamo a valutare l’infinitesimo
e questo
non è possibile perché lo zero è escluso dalle questioni di indistinguibilità.
In pratica ai fini del nostro esercizio, se ci limitiamo a valutare l’infinitesimo
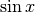 mediante l’infinitesimo x non abbiamo informazioni abbastanza dettagliate.
È come se
mediante l’infinitesimo x non abbiamo informazioni abbastanza dettagliate.
È come se 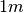 fosse la misura di due oggetti di diversa lunghezza:
con il solo metro non sapremmo apprezzare la differenza e avremmo bisogno di misurarla
a decimetri, o centimetri ecc.
Analogamente, per meglio valutare la differenza fra i due infinitesimi
fosse la misura di due oggetti di diversa lunghezza:
con il solo metro non sapremmo apprezzare la differenza e avremmo bisogno di misurarla
a decimetri, o centimetri ecc.
Analogamente, per meglio valutare la differenza fra i due infinitesimi 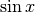 e x ricorriamo al secondo ordine, cioè confrontiamo
e x ricorriamo al secondo ordine, cioè confrontiamo 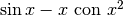 .
.
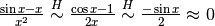 .
.
Quindi nemmeno 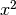 è un’unità di misura
abbastanza infinitesima per misurare la nostra differenza. Dobbiamo ritentare con
è un’unità di misura
abbastanza infinitesima per misurare la nostra differenza. Dobbiamo ritentare con 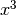 :
:
.
Quindi 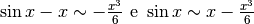 .
.
Infine abbiamo che: 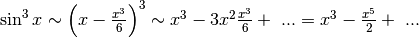 e possiamo trascurare gli ulteriori infinitesimi, che sono di ordine superiore.
e possiamo trascurare gli ulteriori infinitesimi, che sono di ordine superiore.
Tornando all’esercizio:
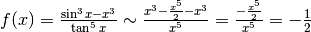 , che è la soluzione già trovata nel Cap.13, ma con molta più fatica.
, che è la soluzione già trovata nel Cap.13, ma con molta più fatica.
Caso generale¶
Dobbiamo valutare il comportamento asintotico di una funzione y=f(x) in un punto a del suo dominio, dove la funzione è derivabile n volte.
Costruzione della regola¶
La funzione è continua, quindi nella monade di a, f(x) è indistinguibile da f(a),
perciò, per 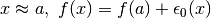 . Si tratta di valutare
l’infinitesimo
. Si tratta di valutare
l’infinitesimo 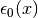 con una scala crescente di
infinitesimi nella monade di a:
con una scala crescente di
infinitesimi nella monade di a: 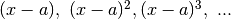 .
Le valutazioni si fanno con i rapporti.
.
Le valutazioni si fanno con i rapporti.
Proviamo dapprima: 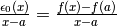 ,
che è sicuramente un rapporto fra due infinitesimi, quindi una forma indeterminata.
Allora:
,
che è sicuramente un rapporto fra due infinitesimi, quindi una forma indeterminata.
Allora: 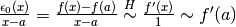 .
.
Dunque 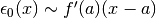 , oppure, per meglio valutare anche
questa indistinguibilità:
, oppure, per meglio valutare anche
questa indistinguibilità: 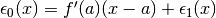 , dove
l’ultimo termine è infinitesimo di ordine superiore rispetto a (x - a).
, dove
l’ultimo termine è infinitesimo di ordine superiore rispetto a (x - a).
Ne consegue che 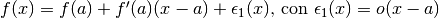 .
.
Poi si prosegue, valutando 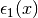 rispetto a
rispetto a 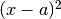 .
.
Per cui 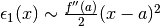 , oppure
, oppure
![\epsilon_1(x)=\frac{f''(a)}{2}(x-a)^2+\epsilon_2(x)\mbox{, con }\epsilon_2(x)=o\left[(x-a)^2\right]](../../../_images/math/8da2e3b80e72bdba7e71332f42092bae4bbc96b6.png) .
.
Fissiamo il risultato raggiunto riscrivendo la funzione:
.
Ora deve essere valutato 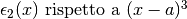 .
.
.
Da questo segue 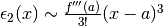 , il che ci porta a :
, il che ci porta a :
![\epsilon_2(x)=\frac{f'''(a)}{3!}(x-a)^3+\epsilon_3(x)\mbox{, con }\epsilon_3(x)=o\left[(x-a)^3\right]](../../../_images/math/a6b1c547f8c5d707181a7c077472a634b3b6eeab.png) .
.
Abbiamo così ulteriormente sviluppato il polinomio che rappresenta la funzione in a
![f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2}(x-a)^2+\frac{f'''(a)}{3!}(x-a)^3+\epsilon_3(x)\mbox{, con }\epsilon_3(x)=o\left[(x-a)^3\right]](../../../_images/math/eb1ae29bb2efebe1b43193ffa39d76ed4d036286.png) .
.
In sintesi¶
Vediamo di capire il percorso e di immaginare lo sviluppo successivo.
Con x nella monade di a, i valori della funzione vengono approssimati con sempre maggiore accuratezza, facendo uso di derivate di ordine crescente e riferiti a potenze crescenti di (x - a).
- Approssimazione di ordine zero:
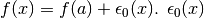 è un infinitesimo.
è un infinitesimo. - Approssimazione di ordine 1:
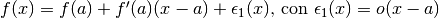 .
. - Approssimazione di ordine 2:
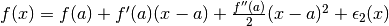 , con
, con ![\epsilon_2(x)=o\left[(x-a)^2\right]](../../../_images/math/e1e1f7e52186df418f3fa3f370cc010162c6edc1.png)
- Approssimazione di ordine 3:
, con
.
Si può riscrivere la formula pensando che 1 = 0! = 1!, 2 = 2! e che la derivata di ordine zero equivale alla funzione:
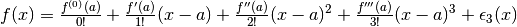
.
Per l’approssimazione di ordine 4 è sufficiente aggiungere
alla formula dell’approssimazione di ordine 3 l’espressione di 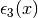 .
.
Lo stesso avviene per le approssimazioni di ordine successivo, fino al grado di approssimazione desiderato.
La regola¶
La formula precedente si può riscrivere in modo sintetico:
![f(x)=\sum_{k=0}^N \frac{f^{(k)}(a)}{k!}(x-a)^k +\epsilon_n(x)\mbox{, con }\epsilon_n(x)=o\left[(x-a)^n\right]](../../../_images/math/d0897301ddfe17f2706f9b2ad1a0b99abc9b7e3f.png) .
.
Il polinomio che ne risulta si dice Polinomio di Taylor di ordine n in forma
infinitesima della funzione 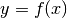 nel punto
nel punto  ed esprime la
funzione
ed esprime la
funzione 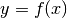 nella monade di a come un polinomio di grado minore
o uguale a
nella monade di a come un polinomio di grado minore
o uguale a 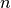 nelle potenze dell’infinitesimo
nelle potenze dell’infinitesimo 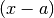 , a meno di
un infinitesimo di ordine superiore
, a meno di
un infinitesimo di ordine superiore 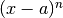 .
.
Note
Parliamo di “polinomio di grado minore o uguale a n”, e non semplicemente di grado uguale, solo perché può succedere, come in alcuni esempi che seguono, che per un certo n la derivata della funzione sia nulla.
Note
Nel caso che a sia zero, lo sviluppo del polinomio avviene per x, al posto di (x - a) e il polinomio viene spesso chiamato con il nome di Polinomio di MacLaurin.
Esercizi e applicazioni¶
- Sviluppa la funzione seno nell’origine.
Per tornare ai calcoli dell’esercizio precedente, sviluppiamo la funzione seno per a = 0, per cui la formula generale risulta:
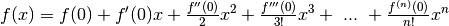 .
.
I coefficienti si ottengono dalla successione delle derivate, calcolate in 0.
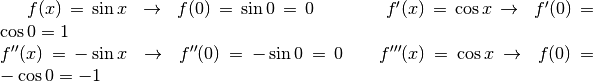
I valori 0, 1, 0 -1 si ripetono. Inseriti nel polinomio, annullano i termini di ordine pari. Per cui l’espressione diventa:
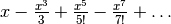
In conclusione, la funzione seno si approssima così, per esempio fino al quinto ordine:
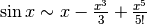 oppure in modo equivalente:
oppure in modo equivalente: 
(in realtà in questo caso 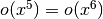 perché le derivate di ordine pari sono uguali a zero).
perché le derivate di ordine pari sono uguali a zero).
- Sviluppa la funzione coseno nell’origine.
Cerchiamo prima i coefficienti:
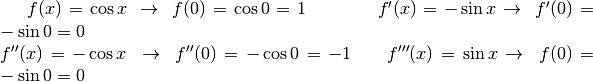
da cui: 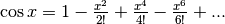
- Sviluppa la funzione esponenziale naturale nell’origine.
Le derivate nello zero valgono 1, quindi: 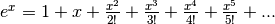
- Sviluppa la funzione
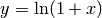 nello zero.
nello zero.
Nel Cap.14 abbiamo già calcolato l’espressione per le derivate successive di questa
funzione: 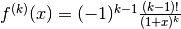 . L’espressione ci serve
per calcolare i coefficienti dello sviluppo in serie, perché nello zero
. L’espressione ci serve
per calcolare i coefficienti dello sviluppo in serie, perché nello zero 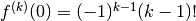 , quindi, dividendo per k! come è richiesto dalla formula di Taylor:
, quindi, dividendo per k! come è richiesto dalla formula di Taylor: 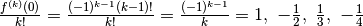 ...
...
Dato che 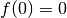 , lo sviluppo nello zero è:
, lo sviluppo nello zero è: 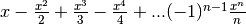 e quindi
e quindi
.
- Sviluppa la funzione
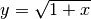 nello zero fino al quarto ordine.
nello zero fino al quarto ordine.
Per evitare calcoli pesanti è meglio riscrivere la funzione come un’esponenziale e calcolare di conseguenza le derivate in zero per esprimere i coefficienti del polinomio.
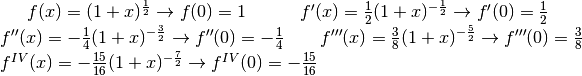
A meno di un infinitesimo di ordine superiore a 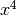 , lo sviluppo
della funzione nello zero è:
, lo sviluppo
della funzione nello zero è:
.
- Studia il comportamento asintotico nello zero di
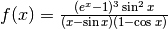 .
.
Nello zero la funzione è una forma indeterminata, un quoziente di infinitesimi. Sviluppiamo il numeratore e il denominatore come polinomi nell’infinitesimo x. Le funzioni vanno sviluppate quanto è utile: per esempio nelle differenze al denominatore le funzioni si sviluppano fino al termine che rende la differenza diversa da zero. Per il numeratore:
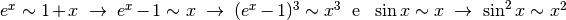 . Quindi, per il numeratore:
. Quindi, per il numeratore: 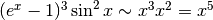 .
.
Per il denominatore, per stimare 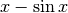 sviluppiamo la funzione seno fino
al terzo ordine e per stimare
sviluppiamo la funzione seno fino
al terzo ordine e per stimare 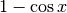 sviluppiamo il coseno fino al secondo:
sviluppiamo il coseno fino al secondo:
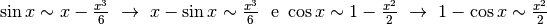 . Quindi, per il denominatore
. Quindi, per il denominatore
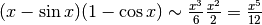
In conclusione abbiamo che: 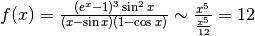 .
.
Confronto fra le due regole¶
- Studia il comportamento asintotico di
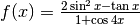 in
in 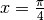
Prima di tutto verifichiamo che si tratta di una forma indeterminata:
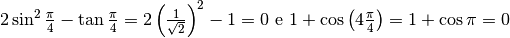 .
Quindi in effetti nel punto desiderato la funzione è quoziente di due infinitesimi
e dobbiamo risolvere la forma indeterminata.
.
Quindi in effetti nel punto desiderato la funzione è quoziente di due infinitesimi
e dobbiamo risolvere la forma indeterminata.
Con la formula di Taylor¶
Se si studia il comportamento asintotico di una funzione nello zero, come negli
esempi svolti fin qui, esprimere il polinomio di Taylor è abbastanza semplice.
Questo esercizio è diverso: il polinomio può essere sviluppato secondo la definizione,
oppure si può operare una sostituzione di variabile in modo da ricondursi al caso
più semplice, così:
posto 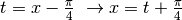 , si sostituisce x nella
funzione, che diventa:
, si sostituisce x nella
funzione, che diventa: ![\frac{2\sin^2 x-\tan x}{1+\cos 4x}=\frac{2\sin^2\left(t+\frac{\pi}{4}\right)-\tan\left(t+\frac{\pi}{4}\right)}{1+\cos\left[4\left(t+\frac{\pi}{4}\right)\right]}](../../../_images/math/1e649d0180e6e14f4d7eb2b50ad413b3e6c35653.png) , che è comunque una forma indeterminata.
, che è comunque una forma indeterminata.
Per il numeratore: 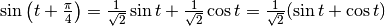 , da cui
, da cui
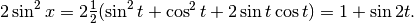
Inoltre: 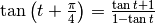
Sviluppiamo solo fino al primo ordine e otteniamo: 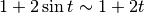 e
e
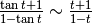 , da cui:
, da cui: 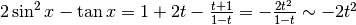 .
.
Per il denominatore: ![1+\cos\left[4\left(t+\frac{\pi}{4}\right)\right]=1+\cos(4t+\pi)=1-\cos 4t\sim 1-\left(1-\frac{16t^2}{2}\right)=8t^2](../../../_images/math/54cd453c70ce731af79424033ae2702900a2a951.png) .
.
Quindi: 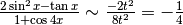 ,
per cui
,
per cui 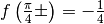 .
.
Con la regola di de l’Hôpital¶
Abbiamo risolto l’esercizio con la formula di Taylor al primo ordine, quando potrebbe bastare la regola di de l’Hôpital. Vediamo:
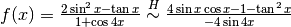 ,
che però è ancora una forma indeterminata per
,
che però è ancora una forma indeterminata per 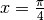 .
Applichiamo di nuovo la regola:
.
Applichiamo di nuovo la regola: 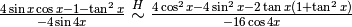 .
.
In 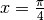 , il numeratore
, il numeratore 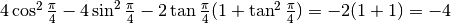 .
.
Il denominatore: 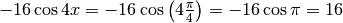 .
E facendo il rapporto fra numeratore e denominatore si torna al risultato già trovato.
.
E facendo il rapporto fra numeratore e denominatore si torna al risultato già trovato.
Esercizio impegnativo.¶
- Sviluppa la funzione
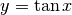 nello zero fino al settimo ordine.
nello zero fino al settimo ordine.
Se si calcolano i coefficienti del Polinomio di Taylor, impegnandosi con diligenza nelle derivate successive fino al settimo ordine, ben presto i calcoli diventano ingestibili. Perciò dopo le prime derivazioni, facciamoci guidare da una linea di ragionamento diversa.
Nello zero le derivate seconda e quarta di tan x valgono zero (provare per credere!). Da questo si intuisce, e lo dimostreremo al termine dei calcoli, che lo sviluppo del Polinomio di Taylor nello zero per la funzione tangente ha solo i termini con le potenze dispari, cioé è di questo tipo:
.
Utilizziamo gli sviluppi già calcolati del seno e del coseno:
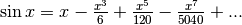 e
e 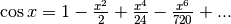 e ricordiamoci che la tangente è il rapporto fra il seno e il coseno:
e ricordiamoci che la tangente è il rapporto fra il seno e il coseno:
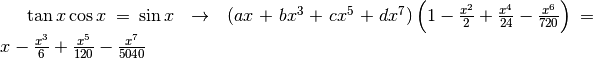 .
.
Possiamo limitare al settimo ordine lo svolgimento dei prodotti a sinistra, quindi raccogliendo i risultati secondo le potenze di x abbiamo :
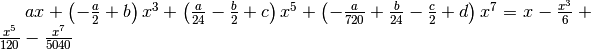 .
.
Confrontando i due membri dell’uguaglianza, perchè questa sia vera deve succedere che
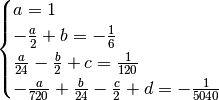
Il sistema non è difficile: si operano le sostituzioni dalla prima riga progressivamente nelle altre. Al termine si ha:
.
Parità e derivate successive¶
Le funzioni dispari, come il seno e la tangente, hanno un grafico simmetrico rispetto all’origine. Quindi il ramo sinistro del grafico è come se risultasse da una rotazione di 180° del ramo destro intorno all’origine. Per questo motivo, le tangenti al grafico in due punti, che si corrispondono nella simmetria, non possono che essere parallele, cioé hanno pendenza uguale. Questo avviene per tutte le coppie di punti del grafico che hanno ascissa opposta. In poche parole le derivate del ramo sinistro, punto dopo punto, sono uguali alle derivate del ramo destro. Concludiamo che la funzione derivata di una funzione dispari è una funzione pari.
Invece le funzioni pari hanno il grafico simmetrico rispetto all’asse y. In questa simmetria le semirette inclinate con una certa pendenza nel semipiano destro si corrispondono con semirette di pendenza opposta nel semipiano sinistro. Quindi le tangenti al ramo destro del grafico hanno pendenza opposta rispetto alle tangenti corrispondenti al ramo sinistro. Insomma la funzione derivata di una funzione pari è una funzione dispari.
La cosa è dimostrabile. Infatti, in una funzione pari 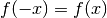 e
in una funzione dispari
e
in una funzione dispari 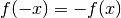 . La derivata di una funzione pari è, calcolata in
. La derivata di una funzione pari è, calcolata in 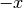 ,
,
per la parità.
Se calcoliamo l’incremento opposto 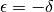
, cioé la derivata è dispari.
Nello stesso modo si dimostra la parità della derivata di una funzione dispari.
Quando si esprime una funzione con il Polinomio di Taylor, si devono calcolare derivate successive di ordine dispari e pari. Come mai lo sviluppo di una funzione, per esempio dispari come il seno, nello zero, contiene solo termini di grado dispari? Perché nello zero si annullano i termini di grado pari? La risposta è che i termini di grado pari contengono derivate che sono funzioni dispari e le funzioni dispari nello zero si annullano. Quindi solo i termini di grado dispari non si annullano perché contengono derivate di ordine dispari, che sono funzioni pari.
Vale lo stesso ragionamento per lo sviluppo nello zero delle funzioni pari, come il coseno, che è fatto solo da termini di grado pari. La derivata prima del coseno è una funzione dispari e sono dispari tutte le derivate successive di ordine dispari. Tutte queste nello zero si annullano, per cui restano solo i termini di grado pari.
Il fatto che la parità degli esponenti in una serie di potenze incarni la parità della funzione è un fatto notevole e suggestivo, non limitato alla monade di zero.
Differenza fra funzioni¶
Come abbiamo visto in alcuni esercizi, con il polinomio di Taylor siamo in grado di stimare la differenza di due funzioni indistinguibili nella monade del punto a, misurandola rispetto alla scala di infinitesimi di ordine crescente data dalle potenze di (x - a).
Stimiamo per esempio la differenza 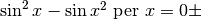 .
Se usassimo la regola nota, che la funzione seno nello zero è asintotica all’angolo,
non faremmo molti progressi. Infatti risulterebbe
.
Se usassimo la regola nota, che la funzione seno nello zero è asintotica all’angolo,
non faremmo molti progressi. Infatti risulterebbe 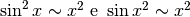 quindi fra le due funzioni non ci sarebbe differenza. Passiamo invece
all’approssimazione di ordine successivo, per cui:
quindi fra le due funzioni non ci sarebbe differenza. Passiamo invece
all’approssimazione di ordine successivo, per cui: 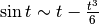 .
Allora:
.
Allora:
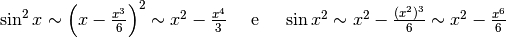 , trascurando i termini successivi nello sviluppo dei quadrati, perché di ordine superiore.
, trascurando i termini successivi nello sviluppo dei quadrati, perché di ordine superiore.
Quindi la differenza, espressa per esempio solo fino al quarto ordine è 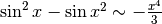 .
.
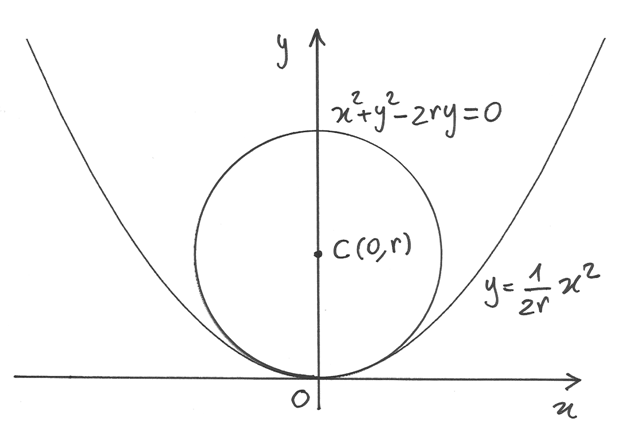
Problema: area del segmento circolare.¶
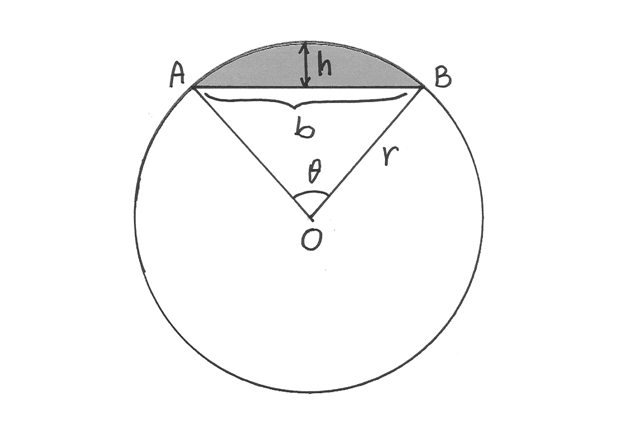
9. Un segmento circolare a una base ha base b e altezza h. Dimostra che l’area del
segmento vale approssimativamente 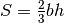 e la formula è tanto più precisa
qanto più b è piccolo rispetto al raggio.
e la formula è tanto più precisa
qanto più b è piccolo rispetto al raggio.
L’area che cerchiamo si può ottenere per differenza fra l’area del settore circolare
e l’area del triangolo. L’area del settore è 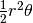 . L’area del
triangolo è
. L’area del
triangolo è
.
Quindi: 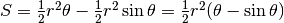
Abbiamo già stimato nell’es.6 la differenza fra l’angolo infinitesimo e il suo seno,
sviluppando quest’ultimo in serie di Taylor fino al terzo ordine. Ricaviamo che
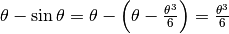 , da cui
, da cui 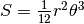 .
.
Vediamo ora il prodotto bh. Per b: 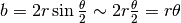 .
.
Invece ![h=r-r\cos\frac{\theta}{2}=r\left(1-cos\frac{\theta}{2}\right)=r\left[1-\left(\frac{\theta^2}{8}\right)\right]=r\frac{\theta^2}{8}](../../../_images/math/8e56561f4abcd725c9e8973f117918d66229b185.png) .
.
Quindi ho che 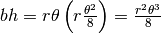 .
Alla fine:
.
Alla fine: 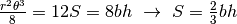 .
.
Ordine di contatto fra due curve¶
Il problema precedente ha una soluzione alternativa immediata, ricordando una delle prime lezioni sugli iperreali, dove si mostrava che una parabola nel suo vertice è indistinguibile da una circonferenza con il centro sull’asse, a distanza doppia del fuoco. Uno dei risultati che se ne ricavavano era che l’area del segmento parabolico è 2/3 dell’area del rettangolo circoscritto. Allora possiamo immaginare che il segmento parabolico sia indistinguibile dal segmento circolare, per cui la formula si dimostra immediatamente.
Il disegno riprende il concetto di tangenza fra due curve. Sappiamo calcolare la tangente a una curva, intesa come retta tangente, e abbiamo imparato a risolvere il problema con la derivata prima. Fra due curve però la tangenza è di ordine diverso e con questo si intende che l’approssimazione fra le due curve nel punto di tangenza è valutata meglio con le derivate di ordine superiore.
Seguendo il disegno, ricaviamo la funzione che rappresenta la semicirconferenza
inferiore. Dalla circonferenza 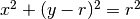 ricaviamo
ricaviamo 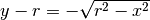 , da cui
, da cui
.
Sviluppiamo il Polinomio di Taylor nello zero (sappiamo già che f(0)=0):
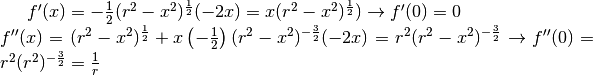
La semicirconferenza è approssimata nello zero dal seguente Polinomio di Taylor:
.
Si tratta proprio della parabola del disegno e questo dimostra che
le due curve sono indistinguibili in zero. Ma quale è l’ordine del contatto?
Se provi a derivare ulteriormente in zero il polinomio, troverai che la derivata
terza si annulla, mentre la derivata quarta 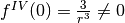 .
Poichè la prima derivata diversa da zero ha ordine 4, diciamo che il contatto è
del terzo ordine. In conclusione, la curva che approssima al meglio la semicirconferenza
è una cubica, non una parabola.
.
Poichè la prima derivata diversa da zero ha ordine 4, diciamo che il contatto è
del terzo ordine. In conclusione, la curva che approssima al meglio la semicirconferenza
è una cubica, non una parabola.
Supponiamo di avere due curve 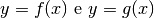 , in contatto nel punto a.
Se si intersecano, allora coincidono in a:
, in contatto nel punto a.
Se si intersecano, allora coincidono in a: 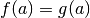 . Se nella monade di a
la loro differenza
. Se nella monade di a
la loro differenza 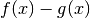 è un infinitesimo di ordine superiore a
è un infinitesimo di ordine superiore a
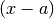 , ma non a
, ma non a 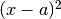 , allora si dice che hanno un contatto del
primo ordine. Se invece
, allora si dice che hanno un contatto del
primo ordine. Se invece 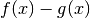 è un infinitesimo di ordine superiore
a
è un infinitesimo di ordine superiore
a 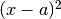 , ma non a
, ma non a 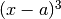 , allora hanno un contatto del secondo
ordine, e così via.
, allora hanno un contatto del secondo
ordine, e così via.
Confrontare la differenza 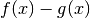 con i vari infinitesimi
con i vari infinitesimi
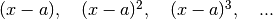 significa calcolare i
coefficienti del Polinomio di Taylor per la differenza delle due funzioni.
Se il contatto è di ordine k la derivata di ordine k + 1 è la prima derivata
che non si annulla.
significa calcolare i
coefficienti del Polinomio di Taylor per la differenza delle due funzioni.
Se il contatto è di ordine k la derivata di ordine k + 1 è la prima derivata
che non si annulla.
Concludendo, possiamo dire che il Polinomio di Taylor di ordine n di una funzione è il polinomio di grado n che in un certo punto ha lo stesso valore della funzione e lo stesso valore delle sue prime derivate di grado minore o uguale a n.
Approssimare una funzione con un polinomio¶
Usiamo il Polinomio di Taylor come seconda funzione e cerchiamo di valutare la differenza fra i valori di una funzione data e la sua espressione secondo Taylor. Abbiamo già visto che per un valore a prefissato una funzione può essere approssimata dal relativo sviluppo con il Polinomio di Taylor, approssimazione più o meno buona a seconda del grado del polinomio. Questa volta valutiamo la differenza in generale, cioé non limitandoci alla monade di un valore a prefissato, ma anche al di fuori di essa. Il polinomio che se ne ricava viene detto Polinomio di Taylor in forma finita.
Inizialmente supponiamo per semplicità a=0 e scriviamo (fino al quarto grado, sempre per semplicità) un polinomio generico, con l’intenzione di portarlo ad approssimare la nostra generica funzione nella monade di zero:
.
Taylor ci indica come esprimere i coefficienti, come abbiamo già visto:
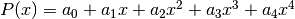
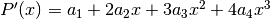
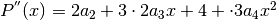
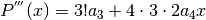
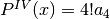
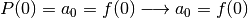
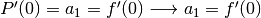
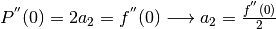
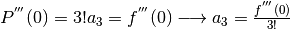
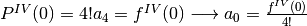
Nel caso di una funzione da approssimare non necessariamente nello zero, l’espressione del polinomio si ottiene con lo stesso procedimento, partendo da:
.
Per capire se in questo modo l’approssimazione è efficace anche al di fuori della monade di a , ricorriamo ad un parallelo cinematico: la funzione f(x) descrive il moto di un punto A sull’asse y. Il punto si allontana dall’origine o si avvicina verticalmente a seconda dei valori x. Invece il Polinomio è rappresentato sull’asse Y da un punto B.
Se il polinomio di Taylor che approssima la funzione è solo di ordine zero, è come se il moto di A fosse approssimato da un moto stazionario: B è fermo nella posizione in cui si trova A per x=a. Solo che, quando x varia, A cambia rapidamente posizione sull’asse y, mentre B resta fermo.
Se il polinomio è di ordine 1, si ha 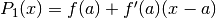 . L’espressione è
analoga alla legge del moto uniforme:
. L’espressione è
analoga alla legge del moto uniforme: 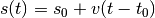 : il punto B si muove
a velocità costante, è sovrapposto al punto A per x=a ed ha la sua stessa velocità.
Per x che si allontana da a, il punto A segue la sua legge di moto vario,
mentre B in generale perderà ben presto il contatto perché la sua velocità è costante.
: il punto B si muove
a velocità costante, è sovrapposto al punto A per x=a ed ha la sua stessa velocità.
Per x che si allontana da a, il punto A segue la sua legge di moto vario,
mentre B in generale perderà ben presto il contatto perché la sua velocità è costante.
Se il polinomio è di ordine 2, si ha 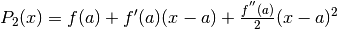 .
L’espressione è analoga alle legge del moto uniformemente accelerato.
Per x=a, i due punti hanno la stessa posizione, la stessa velocità, la stessa
accelerazione e quindi i loro moti si differenziano più lentamente rispetto ai casi precedenti.
.
L’espressione è analoga alle legge del moto uniformemente accelerato.
Per x=a, i due punti hanno la stessa posizione, la stessa velocità, la stessa
accelerazione e quindi i loro moti si differenziano più lentamente rispetto ai casi precedenti.
E’ chiaro come va a finire: con l’approssimazione al terzo ordine i due moti hanno per x=a posizione, velocità, accelerazione e strappo uguali. Solo che A, per valori x diversi da a, è in generale a strappo variabile, di conseguenza si allontana da B, ma più lentamente rispetto a quanto già visto. E così si può procedere per le approssimazioni di ordine superiore.
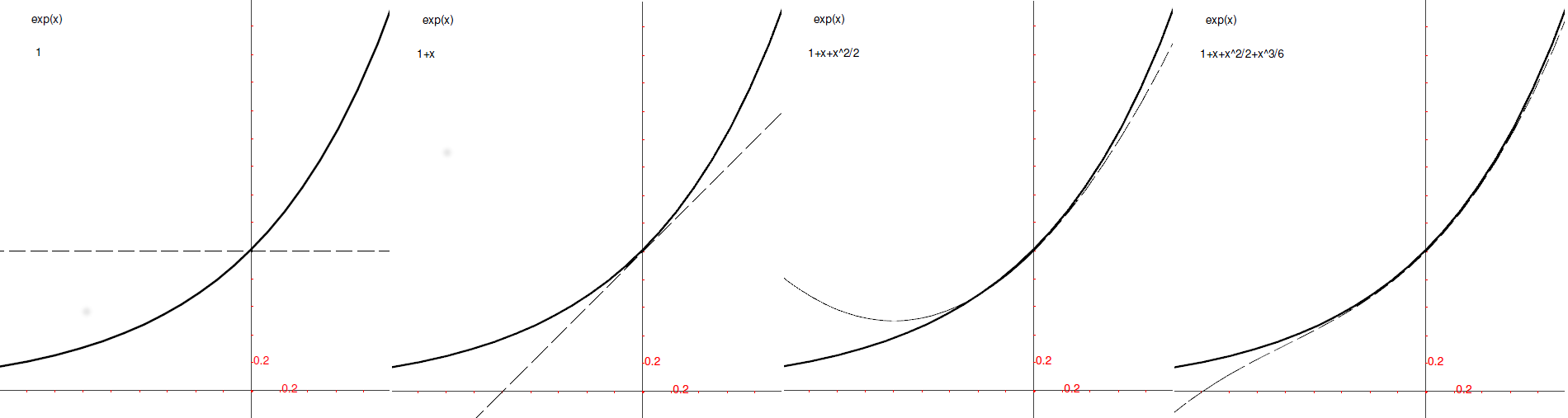
La sostanza è che in un intervallo sufficientemente piccolo, sviluppando adeguatamente il Polinomio di Taylor si ottengono valori sufficientemente vicini a quelli della funzione. Lo si può vedere anche confrontando il grafico della funzione con quello del Polinomio di Taylor associato. Ecco due esempi di funzioni trascendenti.
Il primo caso è quello di 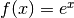 e del suo sviluppo secondo Taylor nello zero.
Nelle quattro immagini la linea continua è la funzione mentre la linea tratteggiata è
il Polinomio.
e del suo sviluppo secondo Taylor nello zero.
Nelle quattro immagini la linea continua è la funzione mentre la linea tratteggiata è
il Polinomio.
La seconda serie riguarda la funzione seno e il polinomio associato, sviluppato fino al settimo ordine. E’ facile accorgersi che man mano che il grado aumenta l’approssimazione migliora anche per valori di x sempre più lontani dallo zero.
Stimare l’errore¶
Cercheremo di dare una stima dell’errore che si commette sostituendo ad una funzione il suo sviluppo secondo Taylor, fino ad un certo grado. Così facendo incontreremo alcuni concetti nuovi ed utili.
Riprendiamo l’esempio del moto rettilineo di un punto A sull’asse y, la cui
posizione è definita da  : quindi
: quindi 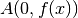 . Si tratta di un moto
rettilineo vario, che inizia al tempo t=a e porta il punto A ad allontanarsi
verticalmente da f(a) secondo la legge f(x-a) che stiamo approssimando con lo
sviluppo del Polinomio di Taylor.
. Si tratta di un moto
rettilineo vario, che inizia al tempo t=a e porta il punto A ad allontanarsi
verticalmente da f(a) secondo la legge f(x-a) che stiamo approssimando con lo
sviluppo del Polinomio di Taylor.
Come riferimento per una prima approssimazione scriviamo per analogia
la legge oraria del moto rettilineo uniforme 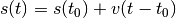 .
Sappiamo che
.
Sappiamo che 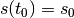 è lo spazio percorso inizialmente, che corrisponde
al valore f(a) della funzione. v è la velocità costante, quindi è anche la
velocità media tenuta dal punto materiale fra
è lo spazio percorso inizialmente, che corrisponde
al valore f(a) della funzione. v è la velocità costante, quindi è anche la
velocità media tenuta dal punto materiale fra 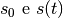 :
:
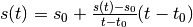 . La sostituzione del simbolo v con
l’espressione della velocità media rende banale tutta la formula, che una volta
semplificata, è un’identità. Solo se conosciamo a priori il valore della velocità
media possiamo dare un senso a questa legge del moto.
. La sostituzione del simbolo v con
l’espressione della velocità media rende banale tutta la formula, che una volta
semplificata, è un’identità. Solo se conosciamo a priori il valore della velocità
media possiamo dare un senso a questa legge del moto.
In effetti però il punto A si muove con una legge più complicata e meno
prevedibile, che approssimiamo un po’ meglio con la formula del moto rettilineo
uniformemente accelerato 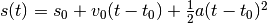 .
Qui la velocità media non compare, compare l’accelerazione
costante che è anche l’accelerazione media tenuta dal punto nell’intervallo
considerato. In ogni caso, per raggiungere la posizione s(t), sicuramente A
si è mosso progressivamente dalla velocità iniziale a quella
finale, raggiungendo e superando una posizione in cui aveva per un istante la
velocità media. Se il moto di A segue una legge più complicata, può succedere che in
quell’intervallo di tempo la velocità media venga raggiunta e superata più volte,
accelerando e decelerando, ma il fatto centrale è che è impossibile evitare
di raggiungere la velocità media almeno una volta.
.
Qui la velocità media non compare, compare l’accelerazione
costante che è anche l’accelerazione media tenuta dal punto nell’intervallo
considerato. In ogni caso, per raggiungere la posizione s(t), sicuramente A
si è mosso progressivamente dalla velocità iniziale a quella
finale, raggiungendo e superando una posizione in cui aveva per un istante la
velocità media. Se il moto di A segue una legge più complicata, può succedere che in
quell’intervallo di tempo la velocità media venga raggiunta e superata più volte,
accelerando e decelerando, ma il fatto centrale è che è impossibile evitare
di raggiungere la velocità media almeno una volta.
Seguiamo lo stesso ragionamento con il Polinomio di Taylor. La funzione viene
sviluppata al primo ordine in forma finita approssimativamente con
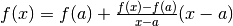 . Portando a sinistra f(a) si esprime
l’errore di valutazione che si farebbe se fermasse lo sviluppo del Polinomio all’ordine
zero:
. Portando a sinistra f(a) si esprime
l’errore di valutazione che si farebbe se fermasse lo sviluppo del Polinomio all’ordine
zero: 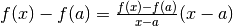 .
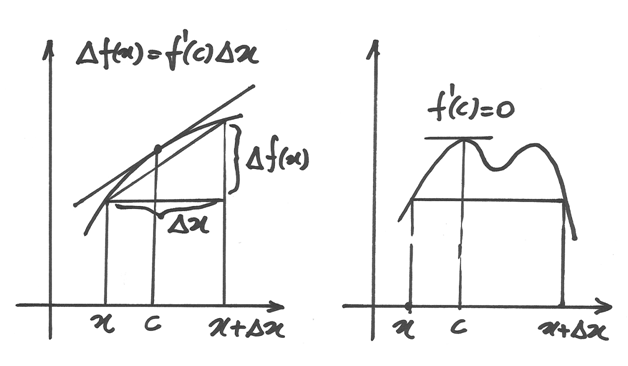
Ora, f(x) è continua, quindi assume tutti i valori f(c) mentre c varia fra
a e x. C’è almeno un c per il quale
.
Ora, f(x) è continua, quindi assume tutti i valori f(c) mentre c varia fra
a e x. C’è almeno un c per il quale
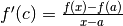 ,
cioé la velocità istantanea del punto risulta uguale a quella media. Allora l’errore
si può stimare con l’espressione:
,
cioé la velocità istantanea del punto risulta uguale a quella media. Allora l’errore
si può stimare con l’espressione: 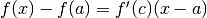 .
Noi non conosciamo l’esatta posizione di c (d’altra parte, se la conoscessimo,
non parleremmo più di approssimazione), sappiamo solo che deve esistere.
.
Noi non conosciamo l’esatta posizione di c (d’altra parte, se la conoscessimo,
non parleremmo più di approssimazione), sappiamo solo che deve esistere.
Proseguiamo nello sviluppo del polinomio, come abbiamo fatto per il moto uniformemente
accelerato 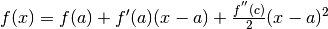 .
Questo vuol dire che se ci fossimo fermati al primo ordine, l’errore sarebbe stato
.
Questo vuol dire che se ci fossimo fermati al primo ordine, l’errore sarebbe stato
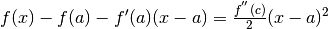 . Per le stesse considerazioni
precedenti, è sicura l’esistenza di almeno un valore c fra a e x in cui
l’accelerazione media è uguale a quella istantanea.
. Per le stesse considerazioni
precedenti, è sicura l’esistenza di almeno un valore c fra a e x in cui
l’accelerazione media è uguale a quella istantanea.
Proseguendo nello sviluppo, le considerazioni si ripetono.
In conclusione, sviluppando il Polinomio di Taylor fino all’ordine n, si
commette un errore espresso da: 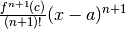 .
La formula non ha soltanto un significato teorico, dato che il punto c non
è a priori conosciuto. Essa è anche utile in situazioni concrete, per esempio
quando si desidera che l’errore non superi un valore piccolo prefissato e
grazie alla formula si determina l’ordine n di sviluppo del Polinomio, che
consente di limitare l’errore.
.
La formula non ha soltanto un significato teorico, dato che il punto c non
è a priori conosciuto. Essa è anche utile in situazioni concrete, per esempio
quando si desidera che l’errore non superi un valore piccolo prefissato e
grazie alla formula si determina l’ordine n di sviluppo del Polinomio, che
consente di limitare l’errore.
Teoremi di Lagrange e di Rolle¶
Il Teorema di Lagrange¶
Riprendiamo, con lieve modifica, la formula dell’errore nell’approssimazione di
ordine zero: 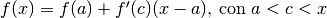 e concentriamoci sul
suo significato geometrico. La formula, riscritta come :
e concentriamoci sul
suo significato geometrico. La formula, riscritta come : 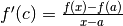 dice che in un punto c dell’intervallo considerato la derivata della
funzione è uguale al coefficiente angolare della secante che passa per gli estremi
dell’intervallo: la tangente per c e la secante per gli estremi sono parallele.
Questa formula esprime il Teorema di Lagrange, secondo il quale l’esistenza di c
che rende vera l’uguaglianza è garantita. I ragionamenti che abbiamo seguito rendono
intuitiva l’esistenza di c e questo per i nostri scopi è sufficiente. Quindi
non daremo una dimostrazione formale del teorema.
dice che in un punto c dell’intervallo considerato la derivata della
funzione è uguale al coefficiente angolare della secante che passa per gli estremi
dell’intervallo: la tangente per c e la secante per gli estremi sono parallele.
Questa formula esprime il Teorema di Lagrange, secondo il quale l’esistenza di c
che rende vera l’uguaglianza è garantita. I ragionamenti che abbiamo seguito rendono
intuitiva l’esistenza di c e questo per i nostri scopi è sufficiente. Quindi
non daremo una dimostrazione formale del teorema.
Riscriviamo di nuovo la formula con maggiore sintesi: 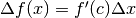 e confrontiamola con quella simile che deriva dallo sviluppo del Polinomio di Taylor:
e confrontiamola con quella simile che deriva dallo sviluppo del Polinomio di Taylor:
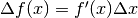 . Dalle considerazioni fatte fin qui
emerge che la seconda formula è approssimata, mentre la prima delle due è una
uguaglianza esatta. La sua importanza risiede nel fatto che il Teorema di Lagrange
garantisce l’esistenza di c.
. Dalle considerazioni fatte fin qui
emerge che la seconda formula è approssimata, mentre la prima delle due è una
uguaglianza esatta. La sua importanza risiede nel fatto che il Teorema di Lagrange
garantisce l’esistenza di c.
Il Teorema di Rolle¶
Una facile conseguenza del Teorema di Lagrange si ottiene se la funzione assume
gli stessi valori agli estremi dell’intervallo, quindi f(x)=f(a), oppure
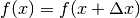 o ancora
o ancora 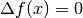 . In questo caso
il teorema diventa: esiste un valore c strettamente compreso fra a e x tale
che in c la derivata si annulla. Dal punto di vista geoometrico si ha che in c
la tangente è orizzontale (come la secante agli estremi). Dal punto di vista cinematico
significa che se il punto ritorna alla posizione di partenza, allora si è fermato
almeno una volta.
. In questo caso
il teorema diventa: esiste un valore c strettamente compreso fra a e x tale
che in c la derivata si annulla. Dal punto di vista geoometrico si ha che in c
la tangente è orizzontale (come la secante agli estremi). Dal punto di vista cinematico
significa che se il punto ritorna alla posizione di partenza, allora si è fermato
almeno una volta.
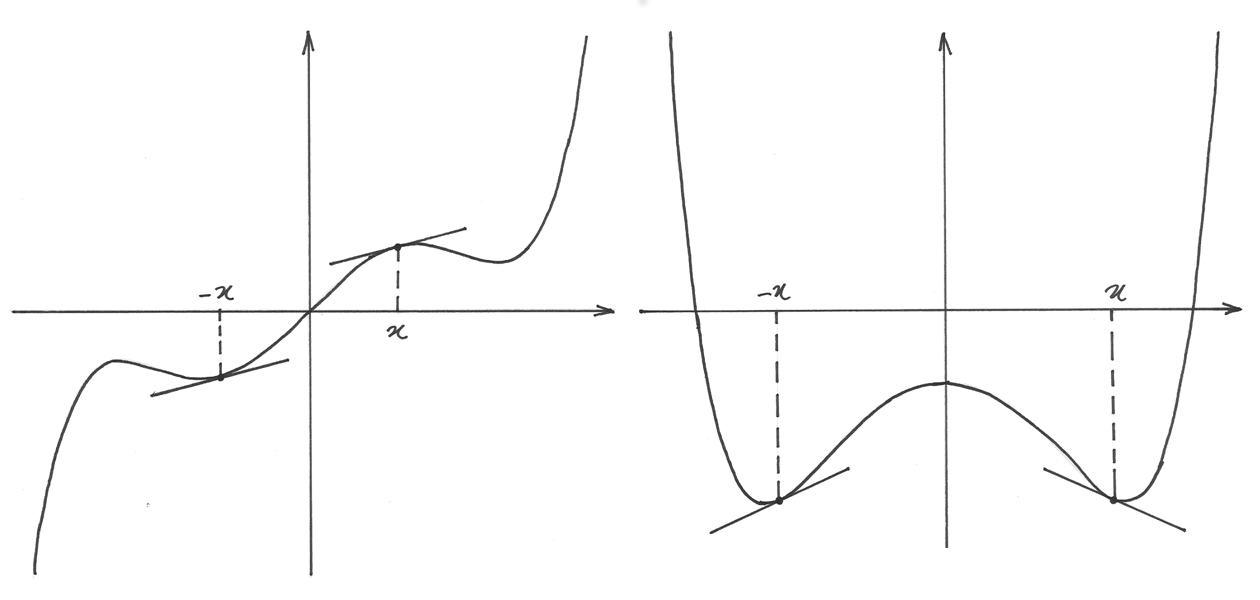
Una prima applicazione¶
Trova tutte le soluzioni dell’equazione 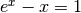 .
.
Una prima soluzione si ottiene in modo empirico: x = 0 è una soluzione perché
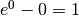 . Per sapere se ci sono altre soluzioni, e eventualmente quali
siano, consideriamo la funzione
. Per sapere se ci sono altre soluzioni, e eventualmente quali
siano, consideriamo la funzione 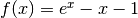 . Cercare i valori per cui si
annulla la funzione è come risolvere l’equazione precedente. Sappiamo già che
. Cercare i valori per cui si
annulla la funzione è come risolvere l’equazione precedente. Sappiamo già che
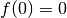 , ora cerchiamo un altro
, ora cerchiamo un altro 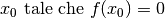 .
Se questo numero esistesse, allora per il Teorema di Rolle esisterebbe anche un
valore c, fra 0 e
.
Se questo numero esistesse, allora per il Teorema di Rolle esisterebbe anche un
valore c, fra 0 e 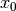 , per cui
, per cui 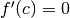 . Ma
. Ma 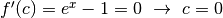 .
In pratica non vi sono altre soluzioni oltre lo zero.
.
In pratica non vi sono altre soluzioni oltre lo zero.
Riassunto¶
- Una funzione
 , sempre derivabile, si può esprimere nella monade di un
valore a del suo dominio, attraverso un polinomio costruito sulla serie di
potenze di (x - a): il Polinomio di Taylor. I coefficienti del polinomio si
ricavano dalle derivate successive della funzione.
, sempre derivabile, si può esprimere nella monade di un
valore a del suo dominio, attraverso un polinomio costruito sulla serie di
potenze di (x - a): il Polinomio di Taylor. I coefficienti del polinomio si
ricavano dalle derivate successive della funzione.
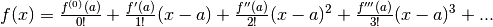
- Più si aggiungono termini al polinomio, più l’approssimazione ai valori esatti della funzione migliora.
- Il Polinomio di Taylor è uno strumento efficace per studiare il comportamento asintotico di una funzione, indispensabile nei casi in cui la Regola di de l’Hôpital non è di aiuto.
- In genere non è necessario sviluppare il polinomio per un numero elevato di termini. Per esempio, nel valutare la differenza fra due funzioni, che è un caso comune, ci si accontenta di scrivere il Polinomio fino al primo termine non nullo, perché i successivi sono infinitesimi di ordine superiore.
- Attraverso semplici ragionamenti sulla simmetria, si deduce che le funzioni pari hanno per derivata una funzione dispari e le funzioni dispari hanno per derivata una funzione pari. Da qui si ricava che il Polinomio di Taylor di una funzione dispari contiene solo termini di ordine dispari e il Polinomio di Taylor di una funzione pari contiene solo termini di ordine pari.
- Quando due curve sono tangenti si può misurare quanto sono indistinguibili nel punto di contatto. Si esprime la differenza delle due funzioni nel punto di contatto con il Polinomio di Taylor, sviluppandola fino al primo termine non nullo. Il grado dell’ultimo termine nullo è l’ordine del contatto fra le due curve in quel punto.
- L’approssimazione che si ha sostituendo alla funzione il suo Polinomio di Taylor è sempre migliore man mano che aumenta il grado del Polinomio, cioé la differenza fra la funzione e il Polinomio si riduce se il grado del Polinomio è maggiore. Questa differenza è indistinguibile da zero nella monade considerata e si accresce man mano che ci si allontana da essa.
- Si può stimare l’errore che si commette approssimando la funzione con il Polinomo di Taylor scritto in forma finita, cioé per qualsiasi x, anche al di fuori di mon(a).
- Il Teorema di Lagrange garantisce che nell’intervallo considerato esiste un punto c per il quale la tangente al grafico della funzione è parallela alla secante che passa per gli estremi dell’intervallo. Il Teorema di Rolle, di conseguenza, assicura che se questa secante è orizzontale, la derivata per c non può che essere nulla.
Esercizi¶
- Sappiamo che una funzione costante ha derivata zero per ogni x. Dimostra che una funzione che ha derivata zero per ogni x è costante.