Le derivate di ordine superiore¶
Differenze seconde e di ordine superiore¶
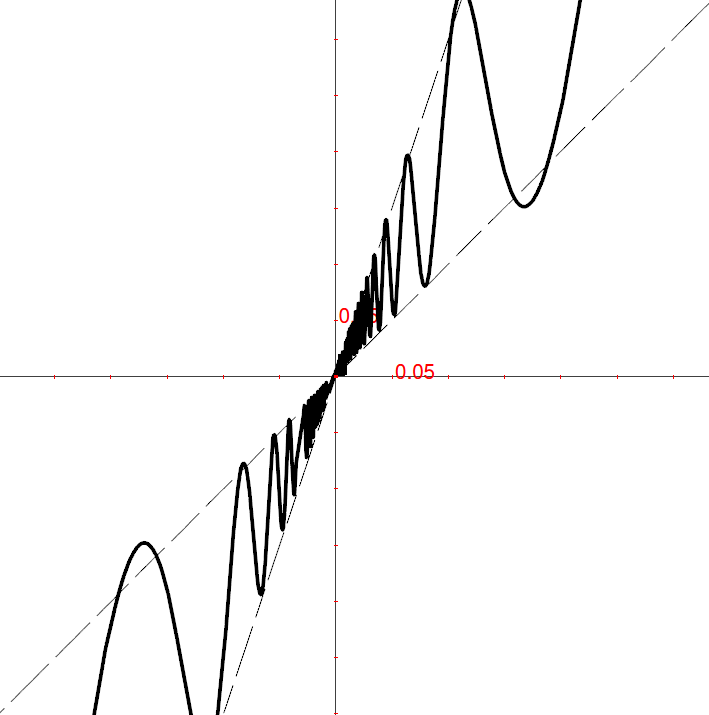
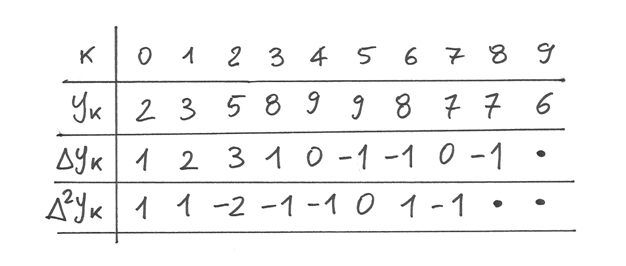
All’inizio del corso abbiamo visto la successione
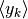 e messo in tabella i suoi valori e le loro differenze. A quella tabella
aggiungiamo una
riga, per elencare le differenze delle differenze, cioè le differenze seconde,
in simboli
e messo in tabella i suoi valori e le loro differenze. A quella tabella
aggiungiamo una
riga, per elencare le differenze delle differenze, cioè le differenze seconde,
in simboli ![\Delta^2y_k=\Delta\left[\Delta y_k\right]=\Delta
y_{k+1}-\Delta y_k](../../../_images/math/679843e01eb7fd131491981baddfd29e88dd3794.png) .
I valori delle differenze seconde si ottengono dalla penultima riga, e
le differenze seconde calcolabili sono una di meno rispetto alle differenze
prime.
.
I valori delle differenze seconde si ottengono dalla penultima riga, e
le differenze seconde calcolabili sono una di meno rispetto alle differenze
prime.
Se troviamo un valore  , vuol dire che
, vuol dire che
 , cioè nella riga superiore si trovano in
corrispondenza due differenze prime
consecutive uguali. A sua volta questo vuol dire che nella seconda riga fra i
tre valori
, cioè nella riga superiore si trovano in
corrispondenza due differenze prime
consecutive uguali. A sua volta questo vuol dire che nella seconda riga fra i
tre valori 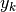 corrispondenti c’è la stessa crescita o lo stesso calo.
Quindi nel grafico della successione i tre punti in questione sono allineati,
perché
i due segmenti consecutivi hanno la stessa pendenza.
corrispondenti c’è la stessa crescita o lo stesso calo.
Quindi nel grafico della successione i tre punti in questione sono allineati,
perché
i due segmenti consecutivi hanno la stessa pendenza.
Se invece 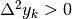 , allora
, allora 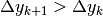 , cioè
i due segmenti hanno pendenza crescente e formano una spezzata concava verso
l’alto,
come i primi 3 punti del grafico. Al contrario, se
, cioè
i due segmenti hanno pendenza crescente e formano una spezzata concava verso
l’alto,
come i primi 3 punti del grafico. Al contrario, se 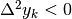 ,
allora
,
allora 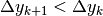 , e la spezzata è concava verso il
basso.
, e la spezzata è concava verso il
basso.
Le differenze seconde coinvolgono necessariamente tre punti consecutivi, come
si vede da
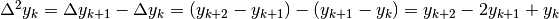 .
Se poi
.
Se poi 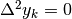 , allora
, allora 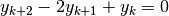 e la
conseguenza è che
e la
conseguenza è che 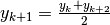 , cioè l’ordinata del
secondo
punto è la media aritmetica delle altre due ordinate. Poiché le ascisse dei tre
punti sono equidistanziate, il secondo punto è il punto medio fra il primo e
il terzo.
, cioè l’ordinata del
secondo
punto è la media aritmetica delle altre due ordinate. Poiché le ascisse dei tre
punti sono equidistanziate, il secondo punto è il punto medio fra il primo e
il terzo.
Dal punto di vista del calcolo, le differenze seconde hanno le stesse regole
delle differenze prime. Quindi, data l’espressione di
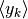 ,
si calcolano le differenze prime con le regole già viste nei capitoli 3 e 4,
poi si applicano di nuovo le stesse regole sull’espressione risultante.
,
si calcolano le differenze prime con le regole già viste nei capitoli 3 e 4,
poi si applicano di nuovo le stesse regole sull’espressione risultante.
Differenze successive¶
Esistono (e a questo punto sono facili da calcolare) anche le differenze terze,
le quarte e così via. Per esempio, non è difficile scoprire che
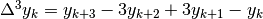 .
.
Abbiamo visto che le differenze prime esprimono l’idea della pendenza dei
segmenti,
le differenze seconde esprimono l’idea della concavità. Per le ulteriori
differenze,
crescendo l’ordine è sempre più arduo dare un significato geometrico al
calcolo.
L’indice che esprime l’ordine della differenza evoca un esponente. Infatti,
guardando l’espressione che sviluppa la differenza di un certo ordine e
confrontandola con l’espressione corrispondente della potenza di un binomio
si scopre che l’analogia è sistematica e puntuale. Per esempio, la differenza
di ordine 4 è:
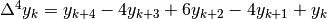 e i suoi coefficienti sono i coefficienti binomiali per l’espressione
e i suoi coefficienti sono i coefficienti binomiali per l’espressione
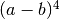 .
L’ordine n della differenza
.
L’ordine n della differenza 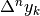 , pur non essendo un
esponente, produce nel risultato i coefficienti che produrrebbe se fosse
l’esponente di un binomio
, pur non essendo un
esponente, produce nel risultato i coefficienti che produrrebbe se fosse
l’esponente di un binomio 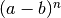 .
.
Rapporti incrementali di ordine superiore¶
Nelle funzioni a dominio discreto¶
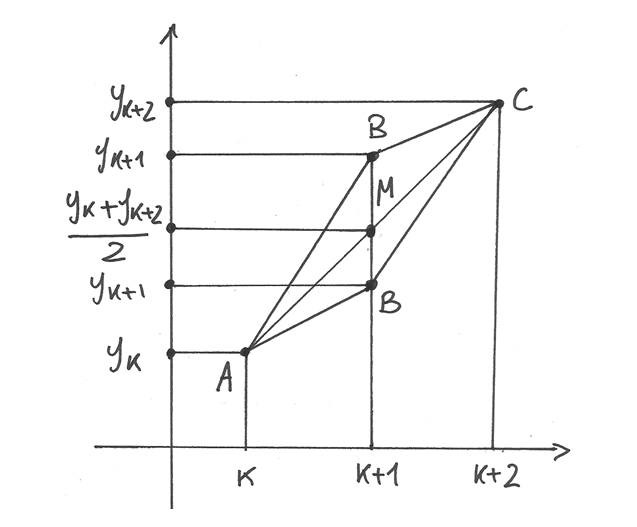
I rapporti incrementali sono i rapporti fra le differenze. I rapporti incrementali di ordine superiore si calcolano per le funzioni a dominio discreto in analogia con quanto abbiamo appena definito.
Data una funzione a dominio discreto
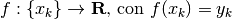 , abbiamo
il rapporto incrementale relativo all’indice k:
, abbiamo
il rapporto incrementale relativo all’indice k:
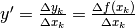 il rapporto incrementale del rapporto incrementale, o rapporto incrementale
secondo:
il rapporto incrementale del rapporto incrementale, o rapporto incrementale
secondo:
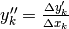 ,
il rapporto incrementale terzo:
,
il rapporto incrementale terzo:
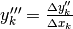 .
.
e così via.
Analogamente a quello che si è visto per la differenza seconda nelle
successioni,
il significato geometrico del rapporto incrementale secondo
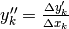 è la concavità della spezzata che unisce tre punti consecutivi della funzione.
Se
è la concavità della spezzata che unisce tre punti consecutivi della funzione.
Se 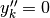 , allora i tre punti sono allineati.
, allora i tre punti sono allineati.
Note
L’analogia stretta fra la differenza nelle successioni e il rapporto
incrementale nelle funzioni a dominio discreto dipende dal fatto che anche la
differenza è un rapporto incrementale, in quanto per le successioni
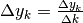 perché
perché 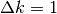 (k è la successione degli indici, vedi Cap.3).
(k è la successione degli indici, vedi Cap.3).
Nelle funzioni a dominio discreto, se nella funzione 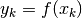 gli incrementi
gli incrementi 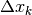 sono fra loro uguali a
sono fra loro uguali a 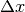 ,
la funzione diventa una successione di ragione
,
la funzione diventa una successione di ragione 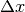 , in cui
l’incremento gioca il ruolo dell’indice. Allora:
, in cui
l’incremento gioca il ruolo dell’indice. Allora:
il rapporto incrementale secondo è:
![y_k''=\frac{\Delta y'_k}{\Delta x}=
\frac{\Delta\left[\frac{\Delta y'_k}{\Delta x}\right]}{\Delta x}=
\frac{\Delta^2 y_k}{(\Delta x)^2}](../../../_images/math/c44d70f319a82392ab8eb13e74cd3b20e101287b.png)
il rapporto incrementale terzo è
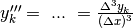 , e così via.
, e così via.
Nelle funzioni a dominio continuo¶
Il rapporto incrementale nelle funzioni a dominio continuo indica il tasso
medio
di variazione 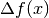 della funzione rispetto all’incremento finito
della funzione rispetto all’incremento finito
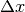 , cioè
, cioè
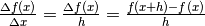 ,
dove abbiamo definito con h quella particolare variazione di x.
,
dove abbiamo definito con h quella particolare variazione di x.
Il rapporto incrementale secondo, potrebbe essere calcolato anche per una
variazione di x eventualmente diversa da h
(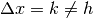 )
ed esprime il tasso medio di variazione del tasso medio di variazione.
)
ed esprime il tasso medio di variazione del tasso medio di variazione.
![\frac{\Delta\left[\frac{\Delta f(x)}{h}\right]}{k}=
\frac{\Delta\left[\frac{f(x+h)-f(x)}{h}\right]}{k}=
\frac{\frac{f(x+h+k)-f(x+h)}{h}-\frac{f(x+k)-f(x)}{h}}{k}=
\frac{f(x+h+k)+f(x+h)-f(x+k)+f(x)}{hk}](../../../_images/math/189045ab865667103e13f70d141952a05a865a9f.png) .
.
Il suo significato geometrico è quello già visto nei casi precedenti. Se il rapporto incrementale secondo è positivo, o negativo, o nullo, la spezzata che unisce i punti del grafico corrispondenti alle ascisse x, x+h, x+h+k è concava verso l’alto, o verso il basso, oppure si tratta di punti allineati.
Se h=k , e quindi i 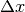 sono uguali, siamo nella situazione più
semplice, cioè al caso delle funzioni a dominio discreto, e possiamo scrivere:
sono uguali, siamo nella situazione più
semplice, cioè al caso delle funzioni a dominio discreto, e possiamo scrivere:
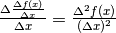 ,
indicando con
,
indicando con
![\Delta^2 f(x)=\Delta[\Delta f(x)]=\Delta[f(x+\Delta x)-f(x)]=\\
=[f(x+2\Delta x)-f(x+\Delta x)]-[f(x+\Delta x)-f(x)]= \\
=f(x+2\Delta x)-2f(x+\Delta x)+f(x)](../../../_images/math/9d42ed0baf19bc56675e1263c61acde99c94c5c5.png) (confronta con il 14.1.1 per i coefficienti).
(confronta con il 14.1.1 per i coefficienti).
Sviluppando il ragionamento come nei casi precedenti, arriviamo al rapporto
incrementale di ordine n: 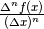 .
.
Derivata seconda e derivate successive¶
Nelle funzioni a dominio continuo abbiamo anche definito il tasso di variazione
puntuale, cioè relativo ad un incremento infinitesimo 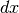 : si tratta
della derivata.
Seguendo le stesse logiche, definiamo:
: si tratta
della derivata.
Seguendo le stesse logiche, definiamo:
La derivata seconda è la derivata della derivata e la indichiamo con
![D[Df(x)]=D^2f(x)=f''(x)](../../../_images/math/471e1ffd39f5ab95d83a1ca8ab273ac366b7362f.png) .
.
E ricordando che la derivata è la parte standard del rapporto differenziale,
quando esso è finito e la parte standard è la stessa per
ogni incremento infinitesimo 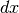 :
:
![Df(x)=st\left[\frac{df(x)}{dx}\right]](../../../_images/math/b88267b5839cc9a3796035224a132b62c2e1c9aa.png) .
.
Possiamo dare la definizione equivalente:
La derivata seconda di  è
è
![D^2f(x)=D[Df(x)]=st\left[\frac{df'(x)}{dx}\right]](../../../_images/math/0587cab2cb8600507aecf29c94b924339efb24cc.png) ,
se la derivata prima è continua, il suo rapporto differenziale è finito e
con la stessa parte standard per qualsiasi incremento infinitesimo
,
se la derivata prima è continua, il suo rapporto differenziale è finito e
con la stessa parte standard per qualsiasi incremento infinitesimo 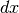 .
.
Calcolare la derivata seconda di una funzione, o anche le derivate successive, purché esistano, è facile: si applicano ripetutamente le regole di derivazione viste nei capitoli precedenti.
Il significato geometrico della derivata seconda è intuibile: ci informa sulla concavità della curva in quel punto (vedi Esempio 5).
La derivata seconda ha una frequente applicazione anche in fisica:
per esempio, poiché la velocità istantanea si calcola derivando l’equazione
del moto, allora la derivata seconda esprime la variazione puntuale della
velocità istantanea, cioè l’accelerazione istantanea.
Infatti, data l’equazione del moto uniformemente accelerato
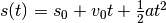 , abbiamo:
, abbiamo:
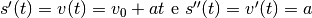 .
.
Esempi¶
Calcolare le derivate successive di
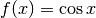 .
.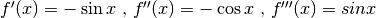 ...
...Quindi le espressioni delle derivate successive dipendono dai resti della divisione per 4.
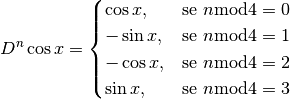
Calcolare
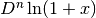
![D\ln(1+x)=\frac{1}{1+x}\\
D^2\ln(1+x)=D\frac{1}{1+x}=-\frac{1}{(1+x)^2}\\
D^3\ln(1+x)=D\left[-\frac{1}{(1+x)^2}\right]=
D\left[-(1+x)^{-2}\right]=2(1+x)^{-3}=\frac{2}{(1+x)^3}\\
D^4\ln(1+x)=D\left[2(1+x)^{-3}\right]=-6(1+x)^{-4}=-\frac{6}{(1+x)^4}\\
\mbox{ ... }\\
D^n\ln(1+x)=\frac{(-1)^{n-1}(n-1)!}{(1+x)^n}](../../../_images/math/9afa6ad84d8146aa45625db3cfa4aa8eca187e24.png) .
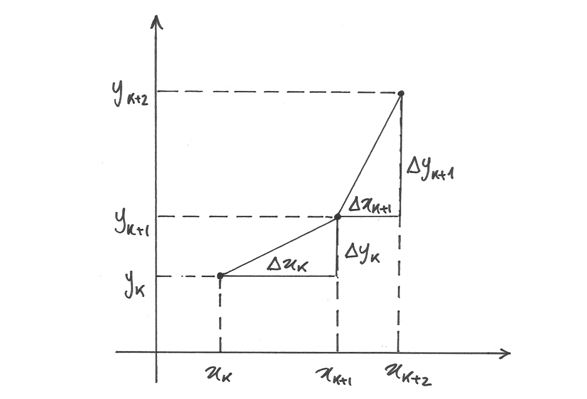
.Ricavare l’accelerazione nella legge oraria del moto armonico.
Il moto armonico è la proiezione sull’asse x del moto circolare uniforme. In questo moto, un punto si muove su una circonferenza di raggio R con velocità angolare
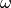 e con angolo iniziale
e con angolo iniziale
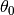 .
L’angolo spazzato dal raggio al tempo t è
.
L’angolo spazzato dal raggio al tempo t è
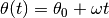 e l’ascissa al tempo t che corrisponde al punto mobile, estremo del raggio,
vale allora:
e l’ascissa al tempo t che corrisponde al punto mobile, estremo del raggio,
vale allora: 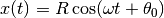 , che è la legge oraria
del moto armonico.
La velocità istantanea è data dalla derivata prima e l’accelerazione dalla
derivata seconda. Quindi
, che è la legge oraria
del moto armonico.
La velocità istantanea è data dalla derivata prima e l’accelerazione dalla
derivata seconda. Quindi
![v(t)=x'(t)=R\left[-\sin(\omega t+ \theta_0)\right]\omega=
-\omega R\sin(\omega t+ \theta_0)](../../../_images/math/eece8f1c518be4756330e619df9078838383599a.png)
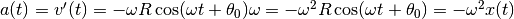 .
.Quale è la concavità della funzione
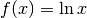 ?
?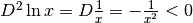 .
La derivata seconda è negativa per ogni x, quindi il grafico della funzione
è concavo verso il basso.
.
La derivata seconda è negativa per ogni x, quindi il grafico della funzione
è concavo verso il basso.
Differenziale secondo e derivata seconda¶
La derivata è stata definita come
![Df(x)=st\left[\frac{df(x)}{dx}\right]](../../../_images/math/b88267b5839cc9a3796035224a132b62c2e1c9aa.png) ,
parte standard del rapporto differenziale, e poi, per semplicità d’uso, abbiamo
convenuto di usare l’uguaglianza semplice
,
parte standard del rapporto differenziale, e poi, per semplicità d’uso, abbiamo
convenuto di usare l’uguaglianza semplice 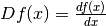 poiché
i due
numeri sono infinitamente vicini.
poiché
i due
numeri sono infinitamente vicini.
Definiamo per analogia il differenziale secondo:
![d^2f(x)=d[df(x)]](../../../_images/math/0a4d930e003234adf7a05a8a65b849bb451746ba.png) . Nel caso più generale, gli incrementi relativi ai due
differenziali sono diversi, per cui si ha
. Nel caso più generale, gli incrementi relativi ai due
differenziali sono diversi, per cui si ha
![d^2f(x)=d[f(x+\delta)-f(x)]=
[f(x+\delta+\epsilon)-f(x+\delta)]-[f(x+\epsilon)-f(x)]=\\
=f(x+\delta+\epsilon)-f(x+\delta)-f(x+\epsilon)+f(x)](../../../_images/math/059d0edd193f24a198e9a753163a43e28e1e3e80.png) .
.
Ne consegue la definizione di derivata (anche qui per brevità ci limitiamo all’uguaglianza delle parti standard):
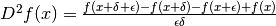
Come sempre, perché la derivata esista, il rapporto differenziale deve essere
finito e indipendente da ogni coppia 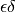 .
Allora la derivata è la parte standard del rapporto differenziale.
Quindi, se la derivata esiste, possiamo ridurci al caso più semplice di
.
Allora la derivata è la parte standard del rapporto differenziale.
Quindi, se la derivata esiste, possiamo ridurci al caso più semplice di
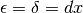 .
Abbiamo:
.
Abbiamo: 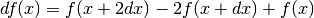 , e la conseguente definizione di
derivata seconda:
, e la conseguente definizione di
derivata seconda:
![D^2f(x)=D\frac{df(x)}{dx}=\frac{d\left[\frac{df(x)}{dx}\right]}{dx}=
\frac{d^2f(x)}{(dx)^2}=\frac{f(x+2dx)-2f(x+dx)+f(x)}{(dx)^2}](../../../_images/math/567fb42456aaa593872df639822ff9599852c3c6.png) .
.
Nessuno si sognerebbe di applicare la definizione di rapporto differenziale per calcolare la derivata seconda: molto più facile e immediato applicare due volte le regole di derivazione.
I discorsi relativi alle derivate di ordine superiore vengono di conseguenza:
la derivata di ordine n è la parte standard del rapporto differenziale
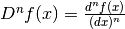 . Si possono omettere le parentesi al
denominatore, pur di ricordarsi che n non è un esponente.
. Si possono omettere le parentesi al
denominatore, pur di ricordarsi che n non è un esponente.
Esercizi impegnativi e un caso patologico¶
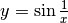 ¶
¶
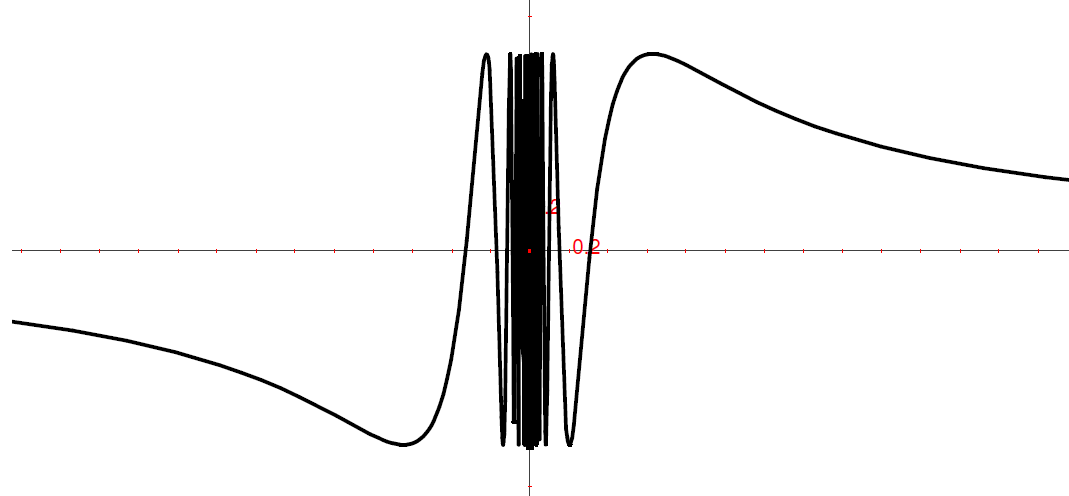
Analizza il comportamento asintotico nello zero di 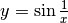 .
.
Se si conosce il grafico di una funzione f(x) si può dedurre il grafico di
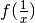 :
:
- per
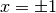 i due grafici coincidono
i due grafici coincidono - per
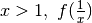 ha lo stesso andamento che ha f(x)
fra 0 e 1.
ha lo stesso andamento che ha f(x)
fra 0 e 1. - per
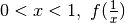 ha lo stesso andamento che ha f(x)
per
ha lo stesso andamento che ha f(x)
per  .
. - con i numeri negativi il discorso è simmetrico.
Nel nostro esercizio:
 .
Quindi per
.
Quindi per 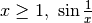 passa da 0.84 a 0.
In particolare, all’infinito
passa da 0.84 a 0.
In particolare, all’infinito
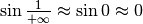 e l’asse x è asintoto orizzontale
e l’asse x è asintoto orizzontale- per
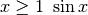 oscilla infinitamente fra -1 e 1,
quindi per
oscilla infinitamente fra -1 e 1,
quindi per 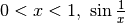 oscilla infinitamente fra -1 e 1.
oscilla infinitamente fra -1 e 1. - il grafico è simmetrico rispetto all’origine perché la funzione è dispari.
Per evidenziare che in zero il comportamento asintotico è irregolare, cerchiamo due infinitesimi sui quali la funzione ha valori con parti standard diverse. Per esempio:
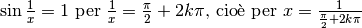 che, se k è un ipernaturale infinito N, risulta
che, se k è un ipernaturale infinito N, risulta
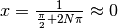 .
.
Invece per 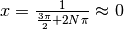 si ha che
si ha che
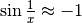 .
In pratica, per N infinito, x è infinitamente vicino a zero e
la funzione assume continuamente valori diversi. La funzione non è definita in
zero.
.
In pratica, per N infinito, x è infinitamente vicino a zero e
la funzione assume continuamente valori diversi. La funzione non è definita in
zero.
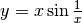 ¶
¶
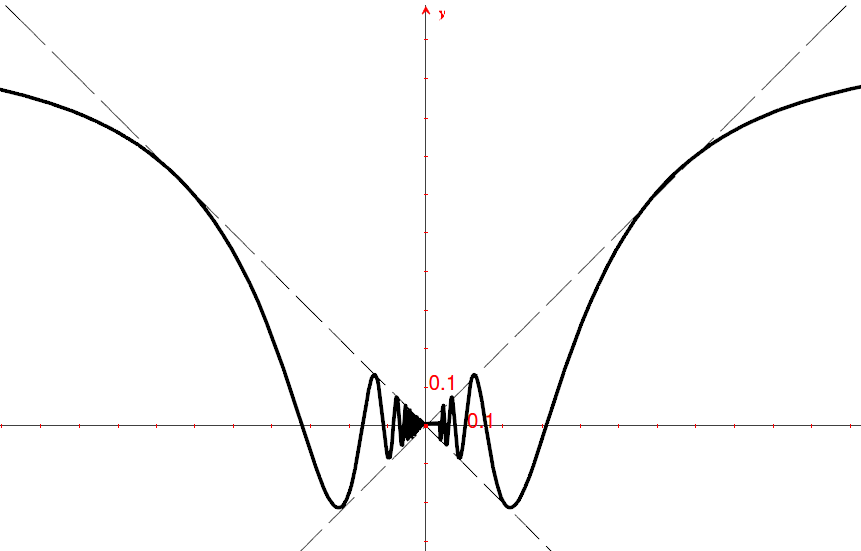
Analizza il comportamento asintotico di 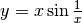 .
.
Visto l’esercizio precedente, in cui la funzione nello zero oscilla fra -1 e 1, è facile concludere che ora f(x) oscilla fra le due rette y = x e y = -x
La funzione è pari, quindi il grafico è simmetrico rispetto all’asse y.
Dato che le due rette che limitano il grafico della funzione attraversano
l’origine, 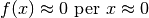 .
Possiamo quindi rendere continua la funzione, ponendo
.
Possiamo quindi rendere continua la funzione, ponendo 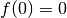 .
.
Vediamo ora se la funzione in zero è derivabile.
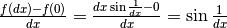 .
Siamo al caso precedente: il rapporto
differenziale assume infinite volte valori fra -1 e 1: la funzione non è
derivabile. Se vogliamo avere una funzione di questo tipo derivabile in zero,
dobbiamo moltiplicare per x (vedi prossimo esercizio).
.
Siamo al caso precedente: il rapporto
differenziale assume infinite volte valori fra -1 e 1: la funzione non è
derivabile. Se vogliamo avere una funzione di questo tipo derivabile in zero,
dobbiamo moltiplicare per x (vedi prossimo esercizio).
Per completare l’analisi del comportamento asintotico, vediamo cosa succede
all’infinito. Posto 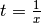 abbiamo
abbiamo
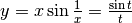 .
È il caso già analizzato nel Cap. 13 e possiamo concludere che all’infinito
(destro ma anche sinistro) il grafico ha un asintoto orizzontale in
.
È il caso già analizzato nel Cap. 13 e possiamo concludere che all’infinito
(destro ma anche sinistro) il grafico ha un asintoto orizzontale in
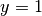 .
.
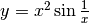 ¶
¶
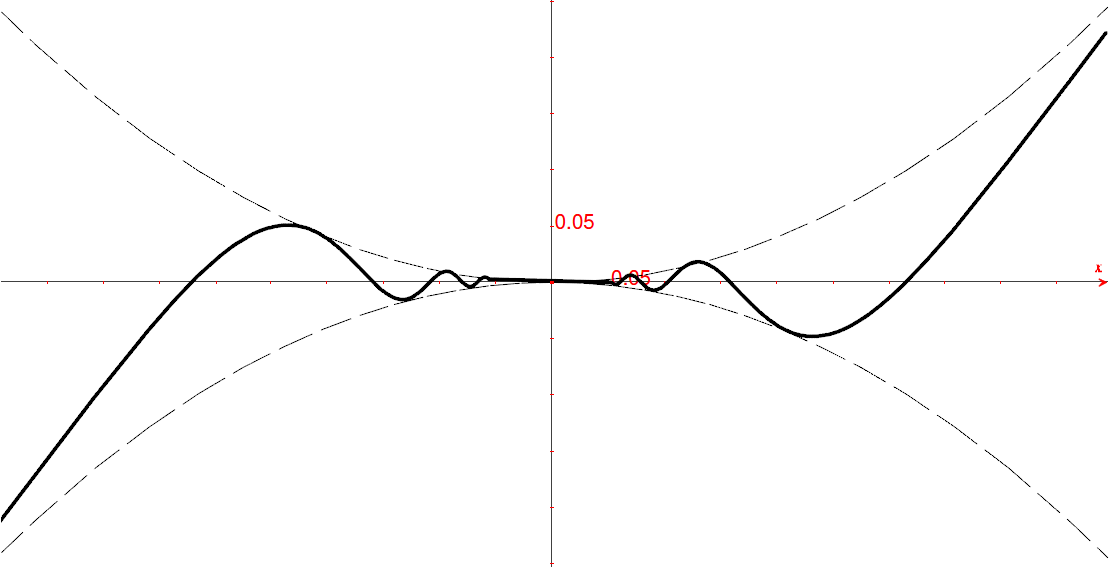
Analizza il comportamento asintotico in zero di 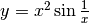 .
.
Facendoci guidare dal caso precedente, vediamo che f(x) è schiacciata fra le due parabole.
Per questo motivo, si può renderla continua imponendo
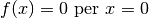 ,
come nell’es.2. Per la derivabilità, vediamo il rapporto differenziale in zero:
,
come nell’es.2. Per la derivabilità, vediamo il rapporto differenziale in zero:
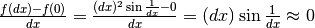 .
.
Quindi 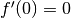 .
.
L’espressione della derivata risulta:
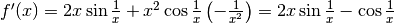 .
.
La derivata seconda nello zero non esiste, perché la derivata prima, per quanto
visto sopra, dipende da 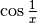 , che ha un comportamento
irregolare.
, che ha un comportamento
irregolare.
Un caso patologico¶
Nella definizione di derivata, in questo caso di derivata seconda, c’è un
dettaglio importante: il rapporto differenziale
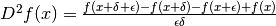 deve avere la stessa parte standard per ogni coppia di infinitesimi
deve avere la stessa parte standard per ogni coppia di infinitesimi
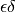 .
Se questo avviene, allora vale anche
.
Se questo avviene, allora vale anche 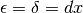 ,
da cui segue la definizione
,
da cui segue la definizione
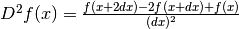 (vale in ogni caso l’approssimazione che ci permette di usare il segno = al
posto di
(vale in ogni caso l’approssimazione che ci permette di usare il segno = al
posto di  ).
).
Ci possono essere funzioni per le quali il rapporto differenziale secondo
ha un comportamento asintotico regolare solo se gli incrementi infinitesimi
sono uguali. Quindi non si può dire che la derivata esiste, perché per
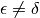 il rapporto differenziale non ha sempre la stessa parte standard.
il rapporto differenziale non ha sempre la stessa parte standard.
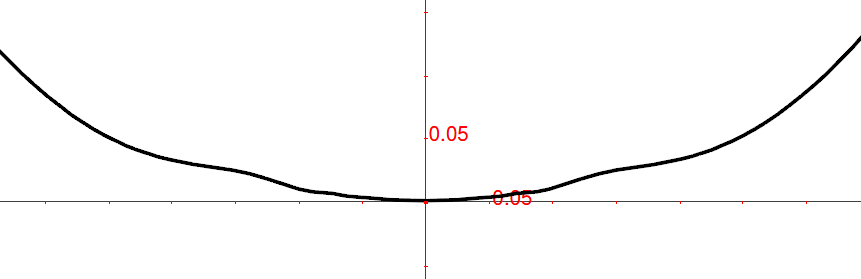
Consideriamo la funzione 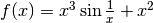 e studiamola sulla
base degli esempi precedenti.
e studiamola sulla
base degli esempi precedenti.
Dal grafico, a prima vista non sembrano esserci questioni particolari, perché i valori oscillano strettamente a cavallo della cubica.
Rendiamo continua f(x) nello zero: 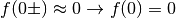 .
Per calcolare le derivate usiamo le definizioni. Per la derivata prima, in zero:
.
Per calcolare le derivate usiamo le definizioni. Per la derivata prima, in zero:
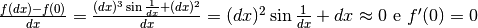 .
.
Per
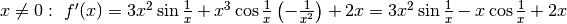 .
.
La derivata nello zero è stretta fra le rette 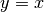 e
e 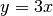
Anche 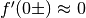 e forse possiamo calcolare la derivata seconda.
Per vedere se esiste:
e forse possiamo calcolare la derivata seconda.
Per vedere se esiste:
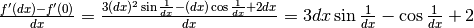 .
.
Il primo termine è infinitamente vicino a zero, mentre il secondo oscilla infinitamente fra -1 e 1 nella monade dello zero. Quindi, se la derivata seconda si calcola derivando la derivata prima, cioè applicando successivamente due incrementi infinitesimi diversi, allora non esiste.
Come secondo tentativo, applichiamo la formula della derivata seconda per
incrementi infinitesimi uguali
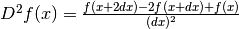 .
.
Per 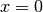 ,
,
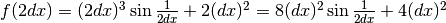
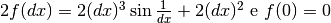 , per cui
, per cui
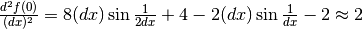
In conclusione, la derivata in zero sembra essere 2, mentre non esiste. Negli esercizi a venire ci occuperemo solo di funzioni prive di questi problemi.
Riassunto¶
- Le differenze seconde per una successione sono le differenze calcolate sulla successione ottenuta dalle differenze prime.
- Analogamente, i rapporti incrementali del secondo ordine per le funzioni a dominio discreto e per le funzioni a dominio continuo vengono calcolati sui rapporti incrementali del primo ordine, seguendo le stesse regole.
- Infine le derivate seconde si calcolano a partire dalle derivate prime, utilizzando le normali regole di derivazione. E tutto questo si ripete per le differenze, i rapporti incrementali e le derivate degli ordini successivi.
- La questione sottile è se per una funzione derivabile esista anche la derivata seconda o le ulteriori derivate. Controllando che esista finito il rapporto differenziale secondo nel punto in questione si risolve l’aspetto della continuità, che è l’aspetto principale e il solo di cui ci occuperemo. Mentre trascureremo il problema di garantire che il rapporto differenziale sia lo stesso per ogni incremento.
- Dal punto di vista grafico, la differenza, il rapporto incrementale e la derivata seconde danno informazioni locali sulla concavità della curva.
Esercizi¶
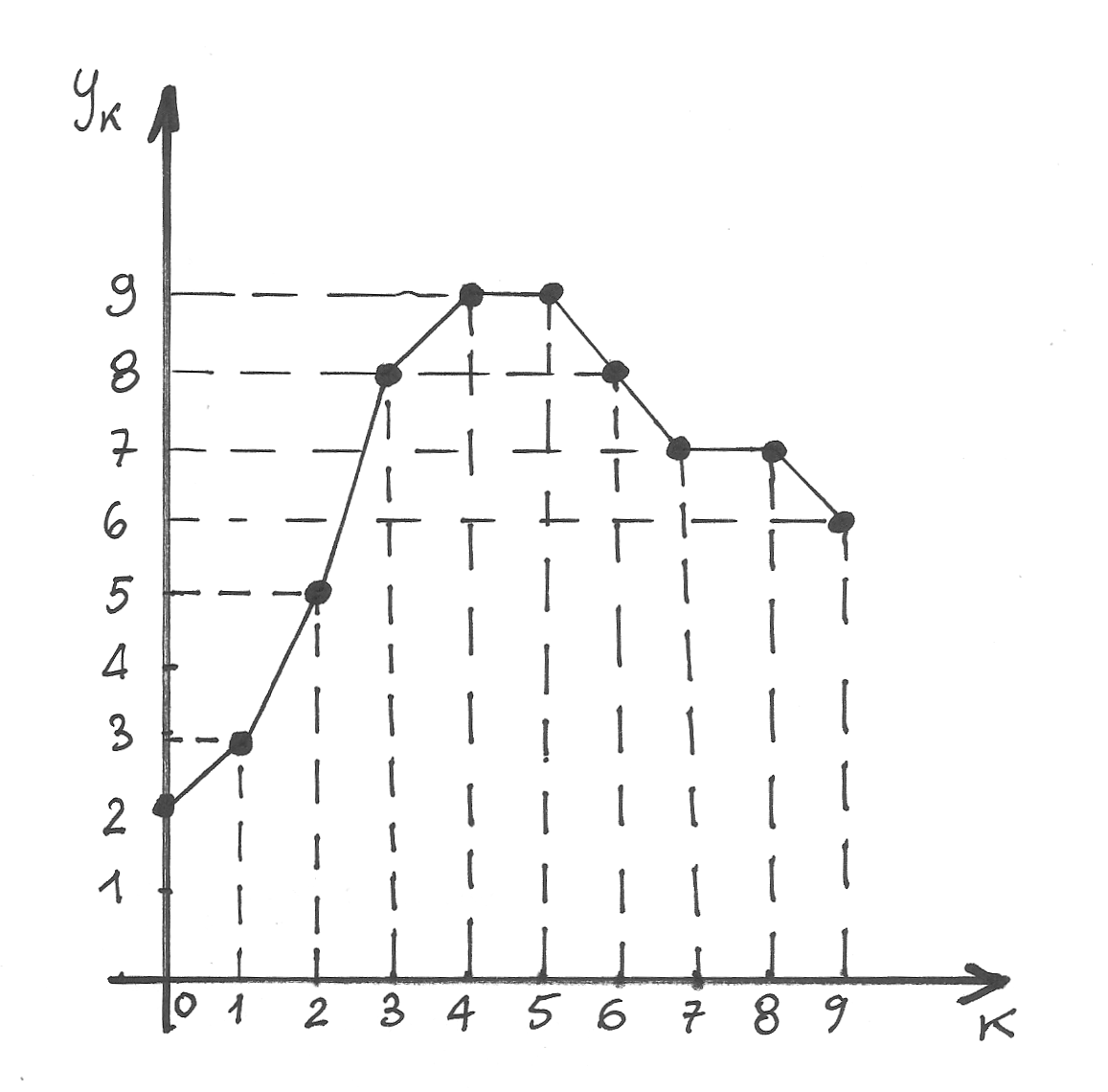
- Per ogni terna consecutiva di punti rappresentati nel primo grafico del capitolo, illustra l’andamento delle differenze seconde.
- Calcolare le derivate successive della funzione seno.
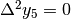 perché i punti sono allineati per
perché i punti sono allineati per 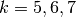 .
.
 .
.