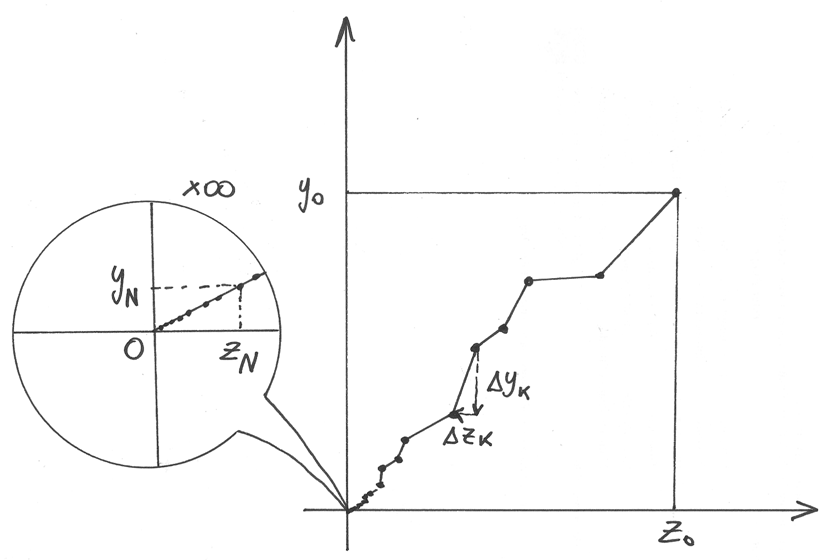
Il comportamento asintotico¶
Convergenza e divergenza delle successioni¶
Iniziamo dall’esempio noto (vedi 12.2): i termini di indice infinito della successione
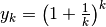 che definisce il Numero di Nepero
hanno tutti la stessa parte standard
che definisce il Numero di Nepero
hanno tutti la stessa parte standard  . Si dice allora che la retta
. Si dice allora che la retta
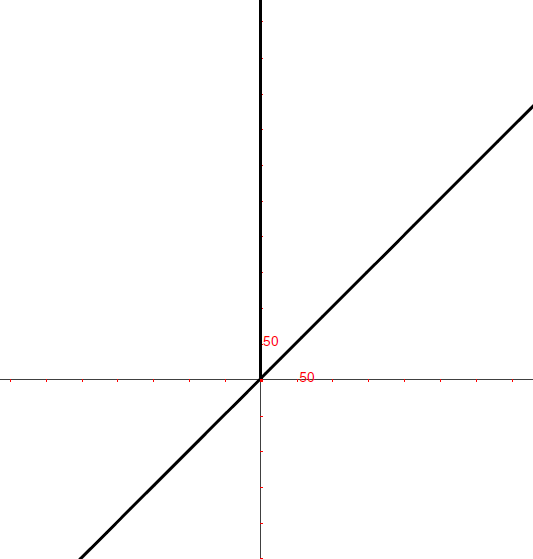
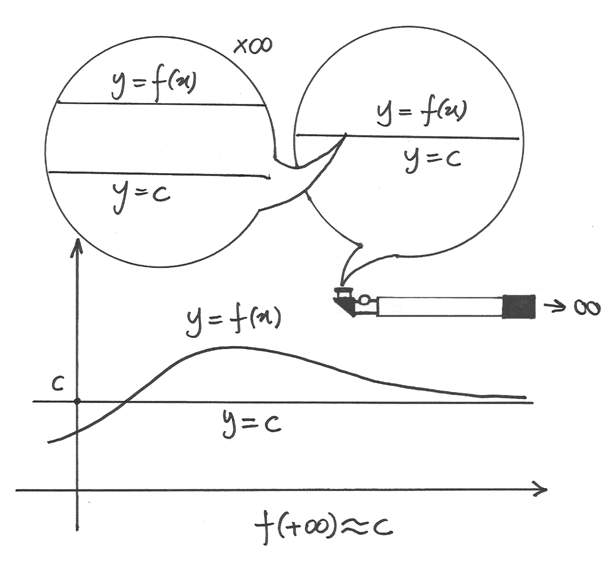
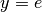 è un asintoto per la successione, cioè i punti del grafico della successione,
per indici infiniti, sono indistinguibili dai punti della retta.
è un asintoto per la successione, cioè i punti del grafico della successione,
per indici infiniti, sono indistinguibili dai punti della retta.
Si dice che la successione è asintoticamente uguale a  . In generale
si dice che una successione
. In generale
si dice che una successione 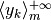 converge
al numero standard
converge
al numero standard  se
se 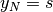 per ogni indice
per ogni indice 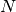 infinito.
infinito.
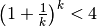 per tutti i naturali k ed è crescente e
il fatto che converga, come vedremo, è un esempio di quanto avviene per tutte le
successioni monotone e limitate.
per tutti i naturali k ed è crescente e
il fatto che converga, come vedremo, è un esempio di quanto avviene per tutte le
successioni monotone e limitate.
Due esempi¶
Le biglie bianche. Qual’è la probabilità di estrarre una biglia bianca da un sacchetto in cui tutte sono bianche, tranne una?
Abbiamo 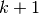 biglie, di cui
biglie, di cui  sono bianche. Con due biglie in tutto
la frazione
sono bianche. Con due biglie in tutto
la frazione 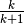 che rappresenta la probabilità in questione, è
prossima a
che rappresenta la probabilità in questione, è
prossima a  . Ma se consideriamo numeri sempre più grandi
troviamo che la successione
. Ma se consideriamo numeri sempre più grandi
troviamo che la successione 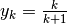 converge
a 1 (oppure che asintoticamente è uguale a 1), dato che
converge
a 1 (oppure che asintoticamente è uguale a 1), dato che
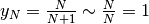 , quando N è ipernaturale infinito.
, quando N è ipernaturale infinito.
L’ordinamento di un vettore.
Per ordinare un vettore  di
di  numeri uso il seguente algoritmo:
confronto il primo elemento con tutti gli altri e se ad ogni confronto lo trovo
maggiore, eseguo lo scambio. Quando ho finito con il primo
elemento, procedo allo stesso modo con il secondo. Questo è l’algoritmo:
numeri uso il seguente algoritmo:
confronto il primo elemento con tutti gli altri e se ad ogni confronto lo trovo
maggiore, eseguo lo scambio. Quando ho finito con il primo
elemento, procedo allo stesso modo con il secondo. Questo è l’algoritmo:
Quale legge collega il numero di confronti 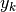 alla lunghezza
alla lunghezza  del vettore?
del vettore?
Per determinare il primo termine devo fare 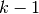 confronti, per il secondo
i confronti sono
confronti, per il secondo
i confronti sono 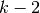 e così via fino al penultimo, che si sistema grazie
ad un confronto. Quindi in tutto i confronti sono
e così via fino al penultimo, che si sistema grazie
ad un confronto. Quindi in tutto i confronti sono
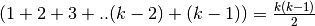 .
Immaginiamo un vettore infinito. Allora
.
Immaginiamo un vettore infinito. Allora
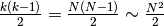 , cioè il numero di confronti diverge positivamente ed è asintotico a
, cioè il numero di confronti diverge positivamente ed è asintotico a
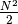
Diciamo che una successione 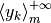 diverge positivamente (negativamente) se per ogni indice infinito
diverge positivamente (negativamente) se per ogni indice infinito 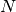 si
ha
si
ha 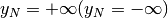 .
.
Criterio per le successioni monotone¶
Teorema. Se una successione è crescente, il suo comportamento asintotico ha solo due possibilità: o diverge positivamente o converge. Le due situazioni appena descritte esemplificano questo teorema, che dimostriamo. Dobbiamo provare che i termini di indice infinito o sono infiniti oppure hanno tutti la stessa parte standard.
a) La successione diverge, supponiamo positivamente: cioè per i termini di indice
infinito vale 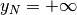 . Se per assurdo non fosse così, allora esisterebbe
un indice
. Se per assurdo non fosse così, allora esisterebbe
un indice 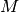 per cui
per cui 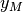 è finito, cioè esisterebbe un numero
standard
è finito, cioè esisterebbe un numero
standard  tale che
tale che 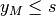 . Dato che la successione è
crescente, si ha che
. Dato che la successione è
crescente, si ha che 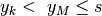 per tutti gli indici naturali
per tutti gli indici naturali  .
Ora questo non è possibile che valga solo per gli indici naturali, deve
valere anche per gli ipernaturali, quindi anche per
.
Ora questo non è possibile che valga solo per gli indici naturali, deve
valere anche per gli ipernaturali, quindi anche per 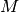 e questo contraddice
l’ipotesi. In conclusione se un termine con indice infinito è infinito, lo sono anche
gli altri con indice infinito.
e questo contraddice
l’ipotesi. In conclusione se un termine con indice infinito è infinito, lo sono anche
gli altri con indice infinito.
b) Escludendo il caso a), la successione non diverge. Mostriamo allora che
i termini di indici infinito hanno la stessa parte standard.
Se, per assurdo, esistessero due indici infiniti
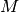 e
e 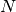 , con
, con 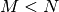 tali che
tali che
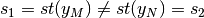 allora
allora 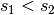 perché la successione
è crescente. Fra i due numeri potrebbe allora esistere un
perché la successione
è crescente. Fra i due numeri potrebbe allora esistere un 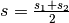 .
Si avrebbe che
.
Si avrebbe che 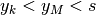 per ogni naturale
per ogni naturale  perché la successione è crescente. Dovrebbe valere lo stesso anche per l’indice
infinito
perché la successione è crescente. Dovrebbe valere lo stesso anche per l’indice
infinito 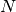 . Dato che
. Dato che 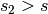 questo è assurdo. In conclusione se
la successione è crescente e non diverge, non può che convergere allo stesso valore.
questo è assurdo. In conclusione se
la successione è crescente e non diverge, non può che convergere allo stesso valore.
Dalla doppia dimostrazione precedente ricaviamo una regola fondamentale: se una successione monotona è limitata, allora converge.
Tutto questo si applica in modo analogo alle successioni non decrescenti e anche
a quelle decrescenti o non crescenti. Queste due ultime o convergono o divergono
a 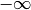 .
.
In generale una successione non ha un comportamento asintotico come quelli descritti,
perché non è detto che sia monotona. Per esempio la successione
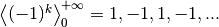 , vale 1 se
, vale 1 se  è pari, -1 se
è pari, -1 se  è dispari, quindi oscilla senza convergere, nemmeno all’infinito.
Invece la successione
è dispari, quindi oscilla senza convergere, nemmeno all’infinito.
Invece la successione 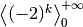 ,
per
,
per 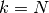 oscilla fra l’infinito positivo e quello negativo, a seconda
della parità di
oscilla fra l’infinito positivo e quello negativo, a seconda
della parità di 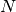 .
Un comportamento ancora diverso è quello della successione
.
Un comportamento ancora diverso è quello della successione 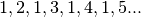 ,
che alterna il comportamento convergente,a quello divergente, a seconda dell’indice.
In conclusione, cerchiamo un criterio da applicare (anche) alle successioni
non monotone, per identificarne il comportamento asintotico in modo stringente.
,
che alterna il comportamento convergente,a quello divergente, a seconda dell’indice.
In conclusione, cerchiamo un criterio da applicare (anche) alle successioni
non monotone, per identificarne il comportamento asintotico in modo stringente.
Criterio per le successioni esponenziali¶
Teorema. Una successione del tipo 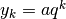 , con
, con  e
e 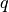 positivi
positivi
- converge a zero se
- converge ad
, se
- diverge positivamente, se
Il primo caso si dimostra in riferimento al terzo caso. Infatti
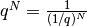 , con
, con 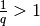 . Poiché
. Poiché
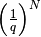 diverge (vedi terzo caso), allora
diverge (vedi terzo caso), allora 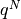 è un infinitesimo. Il secondo caso è banale.
Nel terzo caso, poiché
è un infinitesimo. Il secondo caso è banale.
Nel terzo caso, poiché 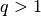 , possiamo scrivere come
, possiamo scrivere come 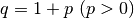 .
Quindi
.
Quindi 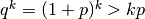 . Allora
. Allora 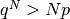 , che è un infinito positivo,
per cui, a maggior ragione, anche
, che è un infinito positivo,
per cui, a maggior ragione, anche 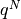 lo è.
lo è.
Criterio del rapporto e gerarchia di infiniti¶
Immaginiamo che il rapporto fra due termini successivi in una successione
a termini positivi 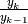 sia asintoticamente uguale a un
numero standard
sia asintoticamente uguale a un
numero standard 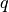 , cioè che valga
, cioè che valga 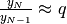 .
.
- Se
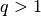 , la successione diverge positivamente.
, la successione diverge positivamente. - Se
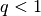 la successione converge a zero,
la successione converge a zero, - mentre nulla si può dire se
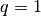 , perché se il rapporto è indistinguibile
da 1, non vuol dire che sia uguale a 1.
, perché se il rapporto è indistinguibile
da 1, non vuol dire che sia uguale a 1.
Proviamo questo criterio sulla successione 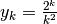 , che vale
all’infinito
, che vale
all’infinito 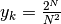 . Il rapporto da analizzare è:
. Il rapporto da analizzare è:
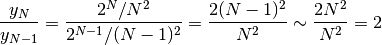
Quindi la successione 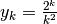 diverge positivamente.
diverge positivamente.
Una conseguenza di questo comportamento asintotico è che 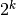 è un
infinito di ordine superiore a
è un
infinito di ordine superiore a 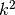 . Anzi, si può dimostrare, più in
generale, che se
. Anzi, si può dimostrare, più in
generale, che se  , allora
, allora 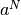 è un infinito di ordine superiore
rispetto a
è un infinito di ordine superiore
rispetto a 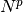 : l’esponenziale, se la base è maggiore di 1,
è un infinito di ordine superiore rispetto a qualsiasi potenza con la stessa base.
: l’esponenziale, se la base è maggiore di 1,
è un infinito di ordine superiore rispetto a qualsiasi potenza con la stessa base.
Per capire quali successioni hanno un comportamento asintotico superiore
ad altre, proviamo alcuni confronti. Per esempio confrontiamo 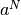 con
con 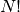 , usando il criterio del rapporto per la successione
, usando il criterio del rapporto per la successione
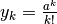 .
Abbiamo
.
Abbiamo
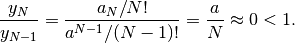
Poiché il rapporto converge a zero, il denominatore, cioè 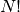 , è un infinito
di ordine superiore.
, è un infinito
di ordine superiore.
Effettuati tutti i confronti, la gerarchia in ordine crescente risulta:
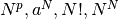 .
.
Note
Il criterio del rapporto non vale al contrario: se la successione diverge
non è detto che il rapporto sia 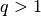 e se converge a zero non è detto che sia
e se converge a zero non è detto che sia
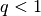 . C’è infatti il rischio che il rapporto risulti indistinguibile da 1,
come nei casi di
. C’è infatti il rischio che il rapporto risulti indistinguibile da 1,
come nei casi di 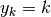 e
e 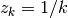
Criterio della radice¶
A volte si ottengono utili indicazioni sul comportamento asintotico di una successione
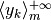 a termini positivi, calcolando la radice
ennesima
dei termini infiniti
a termini positivi, calcolando la radice
ennesima
dei termini infiniti 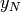 .
.
Se per ogni 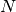 si ha
si ha ![\sqrt[N]{y_n}\approx q](../../../_images/math/f3f8b64596a5eef6e78aa5bd705627491a62ee60.png) , allora
, allora
- se
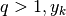 diverge positivamente
diverge positivamente - se
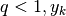 converge a zero
converge a zero
La dimostrazione di questo criterio, che omettiamo, fa riferimento al criterio delle successioni esponenziali.
Criterio del rapporto fra le differenze¶
Il criterio riguarda le successioni che sono quozienti di successioni con lo stesso carattere.
Se 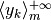 e
e 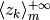 sono successioni entrambe divergenti o entrambe convergenti a zero e se la successione
sono successioni entrambe divergenti o entrambe convergenti a zero e se la successione
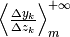 ha un comportamento asintotico regolare, cioè converge o diverge, allora anche
la successione
ha un comportamento asintotico regolare, cioè converge o diverge, allora anche
la successione 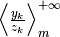 ha lo stesso comportamento asintotico, cioè :
ha lo stesso comportamento asintotico, cioè :
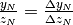 .
La regola vale se le differenze al denominatore hanno tutte lo stesso segno
.
La regola vale se le differenze al denominatore hanno tutte lo stesso segno
Per fare un esempio, consideriamo la successione 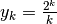 , che è
data dai quozienti di due successioni entrambe divergenti. La regola ci dice che
siccome
, che è
data dai quozienti di due successioni entrambe divergenti. La regola ci dice che
siccome 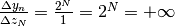 , allora anche
, allora anche
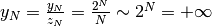
La regola è utile quando la successione asintoticamente è un rapporto fra due infiniti o fra due infinitesimi. Allora si può provare a mettere in rapporto le differenze del numeratore con le differenze del denominatore. Se questo rapporto risulta infinito oppure infinitesimo, anche la successione di partenza ha lo stesso carattere.
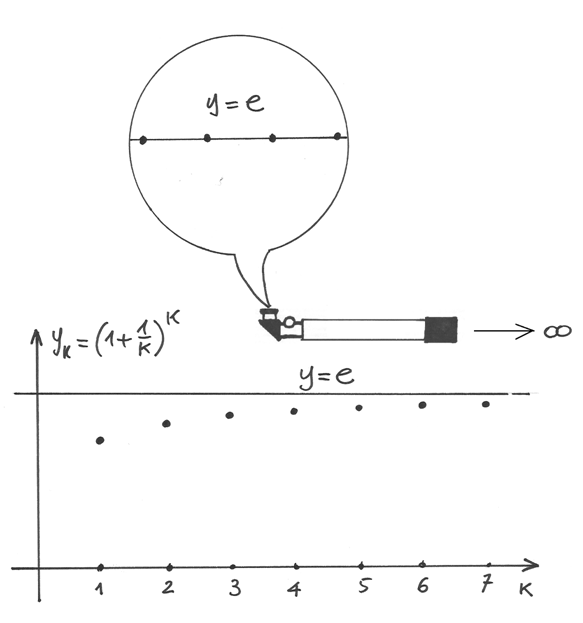
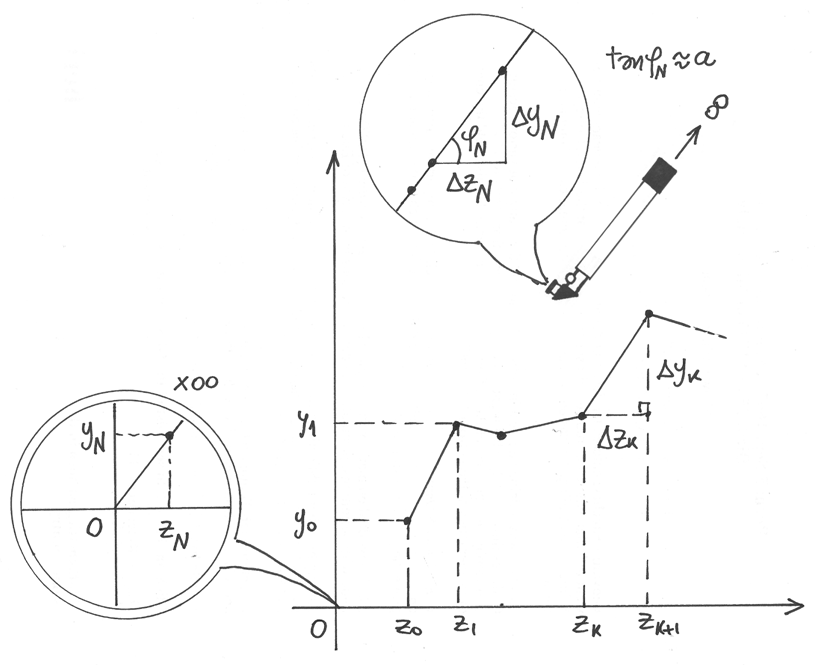
La regola si spiega graficamente. Supponiamo che la successione sia il
rapporto fra 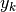 e
e 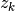 , entrambe divergenti e con le
differenze
, entrambe divergenti e con le
differenze 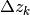 positive e che il rapporto fra le differenze
converga:
positive e che il rapporto fra le differenze
converga: 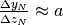 . Mostriamo allora che
converge anche
. Mostriamo allora che
converge anche 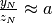 .
.
divergano
Immaginiamo di fissare nel piano cartesiano i punti 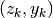 .
Il grafico che risulta è una spezzata che si prolunga verso destra, a causa delle
differenze positive al denominatore. I segmenti di spezzata hanno pendenze date
dai vari
.
Il grafico che risulta è una spezzata che si prolunga verso destra, a causa delle
differenze positive al denominatore. I segmenti di spezzata hanno pendenze date
dai vari 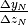 e se queste pendenze all’infinito
convergono, allora uno zoom non standard puntato sull’origine visualizza una semiretta
di pendenza
e se queste pendenze all’infinito
convergono, allora uno zoom non standard puntato sull’origine visualizza una semiretta
di pendenza  che è indistinguibile da una semiretta uscente dall’origine.
Per questo vale asintoticamente che
che è indistinguibile da una semiretta uscente dall’origine.
Per questo vale asintoticamente che 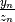 .
Il fatto che la semiretta sembri partire dall’origine dipende dalla visualizzazione
che ci dà lo zoom non standard, come se fosse lontano all’infinito.
.
Il fatto che la semiretta sembri partire dall’origine dipende dalla visualizzazione
che ci dà lo zoom non standard, come se fosse lontano all’infinito.
Lo stesso ragionamento si può fare se le due successioni convergono a zero, utilizzando questa volta un microscopio non standard.
Sperimentiamo la regola sul rapporto 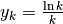 .
Il rapporto delle differenze all’infinito ci dà
.
Il rapporto delle differenze all’infinito ci dà
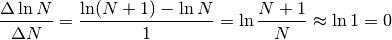
Ne concludiamo che 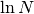 è un infinito di ordine inferiore a
è un infinito di ordine inferiore a 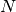 .
.
Convergenza e divergenza delle funzioni¶
Una funzione a dominio continuo può assumere il valore infinito
agli estremi degli intervalli in cui è definita.
In questo caso diremo che la funzione diverge.
Vi sono funzioni che divergono per 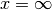 ,
altre che divergono quando
,
altre che divergono quando  appartiene alla monade di un numero finito.
Vi sono invece funzioni che all’infinito, oppure quando
appartiene alla monade di un numero finito.
Vi sono invece funzioni che all’infinito, oppure quando  si avvicina
indefinitamente ad un dato numero finito, assumono valori sempre più vicini a
un valore finito. In questo caso si dice che convergono.
Per studiare i dettagli, iniziamo da qualche esempio.
si avvicina
indefinitamente ad un dato numero finito, assumono valori sempre più vicini a
un valore finito. In questo caso si dice che convergono.
Per studiare i dettagli, iniziamo da qualche esempio.
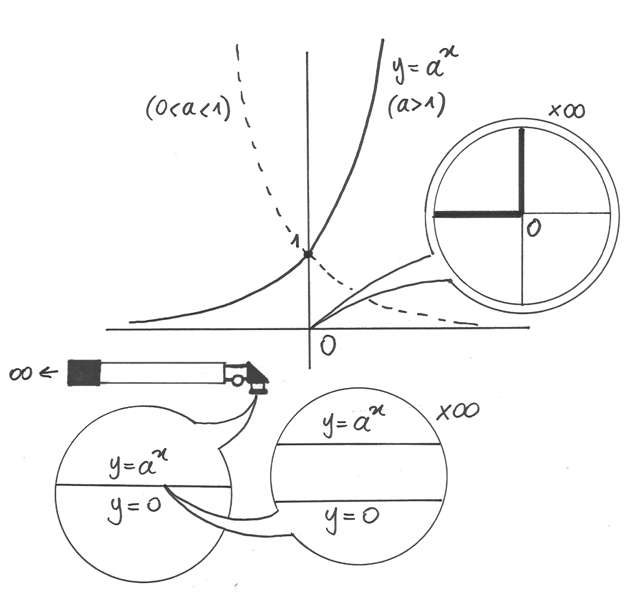
Funzioni esponenziali¶
Abbiamo già visto alcuni esempi di questo comportamento delle funzioni.
Prendiamo per esempio, 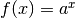 , con
, con  : diverge positivamente
per
: diverge positivamente
per 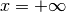 mentre converge a zero per
mentre converge a zero per 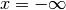 .
Si può anche dire che
.
Si può anche dire che 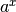 diverge positivamente se x
diverge positivamente ed è infinitesima se x diverge negativamente.
diverge positivamente se x
diverge positivamente ed è infinitesima se x diverge negativamente.
Potremo quindi scrivere sinteticamente per questi due casi:
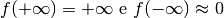 , e quindi, per esempio:
, e quindi, per esempio:
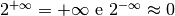
Ancora, una funzione si dice convergere a zero per x che diverge positivamente se per x infinito positivo si ha che f(x) è un infinitesimo. Una funzione si dice che diverge positivamente per x che diverge negativamente se per x infinito negativo si ha che f(x) è un infinito positivo.
Le funzioni divergenti non è detto che divergano solo se diverge la variabile.
Vi sono funzioni il cui dominio esclude particolari valori di x, per esempio
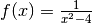 , definita per tutti gli x, tranne
, definita per tutti gli x, tranne 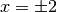 .
In questi casi ci si chiede quale comportamento abbia la funzione se x assume
valori nella monade dei numeri esclusi. Nel nostro esempio, si tratta di
calcolare
.
In questi casi ci si chiede quale comportamento abbia la funzione se x assume
valori nella monade dei numeri esclusi. Nel nostro esempio, si tratta di
calcolare
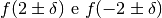 , con
, con 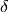 infinitesimo
non nullo. Uno dei calcoli è
infinitesimo
non nullo. Uno dei calcoli è
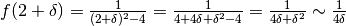 e il risultato è un infinito positivo o
negativo, a seconda del segno di
e il risultato è un infinito positivo o
negativo, a seconda del segno di 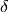 .
Supponiamo per semplicità che
.
Supponiamo per semplicità che
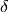 sia positivo, allora avremo
sia positivo, allora avremo
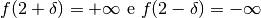 .
Abbiamo quindi una funzione discontinua, che diverge (positivamente
o negativamente, a seconda dei numeri che si considerano) quando la
.
Abbiamo quindi una funzione discontinua, che diverge (positivamente
o negativamente, a seconda dei numeri che si considerano) quando la
 si approssima ai valori
si approssima ai valori 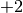 e
e 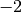 .
.
In questi casi possiamo sottintendere 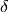 così:
così:
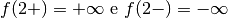 .
Nel primo caso si intende dire che ci approssimiamo a
.
Nel primo caso si intende dire che ci approssimiamo a 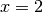 per valori
maggiori di
per valori
maggiori di 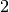 (o da destra), nel secondo caso per valori minori
(da sinistra).
(o da destra), nel secondo caso per valori minori
(da sinistra).
Logaritmi¶
Un secondo esempio di funzione divergente per  che non diverge è la
funzione logaritmo, che diverge negativamente per gli
che non diverge è la
funzione logaritmo, che diverge negativamente per gli  infinitesimi
positivi, oltre a divergere positivamente per
infinitesimi
positivi, oltre a divergere positivamente per  che diverge
positivamente. Scriveremo quindi:
che diverge
positivamente. Scriveremo quindi:
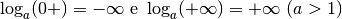 .
.
Funzioni circolari¶
Il seno e il coseno sono funzioni continue e per x divergente mantengono un
comportamento irregolare: oscillante fra i valori 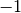 e
e 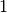 .
Per esempio, la funzione seno vale zero negli infiniti positivi del tipo
.
Per esempio, la funzione seno vale zero negli infiniti positivi del tipo
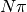 , con
, con 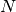 ipernaturale,
mentre vale
ipernaturale,
mentre vale 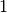 negli infiniti positivi del
tipo
negli infiniti positivi del
tipo 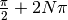 .
.
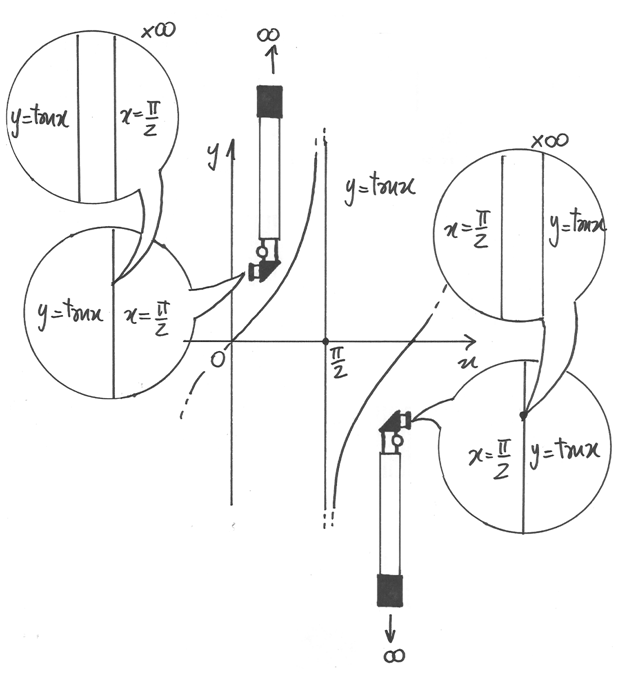
Per la tangente, i punti interessanti sono del tipo 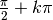 .
Poiché la funzione è periodica, consideriamo solo
.
Poiché la funzione è periodica, consideriamo solo 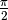 .
.
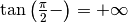 e
e
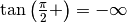 .
Invece per
.
Invece per  che diverge la tangente ha un comportamento
asintotico irregolare.
che diverge la tangente ha un comportamento
asintotico irregolare.
Il comportamento asintotico delle funzioni arcoseno e arcocoseno ...non esiste
perché le funzioni sono continue e definite in un intervallo chiuso. Quindi
mancano i punti di discontinuità nell’intervallo e mancano i punti infiniti per
i quali studiare il comportamento asintotico. Invece l’arcotangente assume
valori infinitamente vicini a 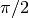 per x che diverge positivamente e
assume valori infinitamente vicini a
per x che diverge positivamente e
assume valori infinitamente vicini a 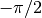 per x che diverge
negativamente:
per x che diverge
negativamente:
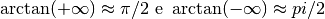 .
Graficamente, questo significa che, grazie a un telescopio non standard
posto orizzontalmente in
.
Graficamente, questo significa che, grazie a un telescopio non standard
posto orizzontalmente in 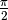 ,
il grafico della funzione arcotangente è indistinguibile da due rette
orizzontali (
,
il grafico della funzione arcotangente è indistinguibile da due rette
orizzontali (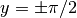 ) e per distinguere il grafico della funzione
dalle rette occorre valersi anche di microscopi non standard.
) e per distinguere il grafico della funzione
dalle rette occorre valersi anche di microscopi non standard.
Un caso notevole¶
La funzione 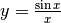 non è definita in
non è definita in 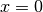 , quindi è
interessante studiare il suo comportamento per valori di x infinitesimi non nulli.
Abbiamo già visto in esempi precedenti che per
, quindi è
interessante studiare il suo comportamento per valori di x infinitesimi non nulli.
Abbiamo già visto in esempi precedenti che per 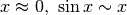 . Quindi avremo
che per
. Quindi avremo
che per 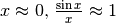 .
Mettendo la funzione in grafico, vediamo che per x che diverge la funzione
è asintotica a zero, perché il denominatore diventa sempre più grande in valore
assoluto e quindi il rapporto
.
Mettendo la funzione in grafico, vediamo che per x che diverge la funzione
è asintotica a zero, perché il denominatore diventa sempre più grande in valore
assoluto e quindi il rapporto 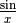 dà risultati sempre più piccoli.
Invece per valori di x molto piccoli, diversi da zero ma prossimi allo zero,
il grafico della funzione si approssima a 1.
Quando una funzione ha questo tipo di comportamento:
dà risultati sempre più piccoli.
Invece per valori di x molto piccoli, diversi da zero ma prossimi allo zero,
il grafico della funzione si approssima a 1.
Quando una funzione ha questo tipo di comportamento: 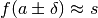 ,
possiamo esprimerci anche in questo modo: per
,
possiamo esprimerci anche in questo modo: per 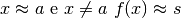 oppure, sinteticamente,
oppure, sinteticamente, 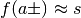 , che nel nostro
caso diventa
, che nel nostro
caso diventa 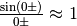 .
.
Per tornare al comportamento della funzione, osserviamo che per 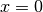 manca il valore della funzione, perché in quel punto non è definita, ma il valore
che manca è prevedibile sulla base delle considerazioni appena fatte. Possiamo
quindi risolvere la discontinuità e imporre
manca il valore della funzione, perché in quel punto non è definita, ma il valore
che manca è prevedibile sulla base delle considerazioni appena fatte. Possiamo
quindi risolvere la discontinuità e imporre 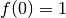 , aggiungendo il
risultato mancante.
In conclusione con il nostro intervento ridefiniamo la funzione in questo modo:
, aggiungendo il
risultato mancante.
In conclusione con il nostro intervento ridefiniamo la funzione in questo modo:
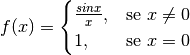
Regola di de L’Hôpital¶
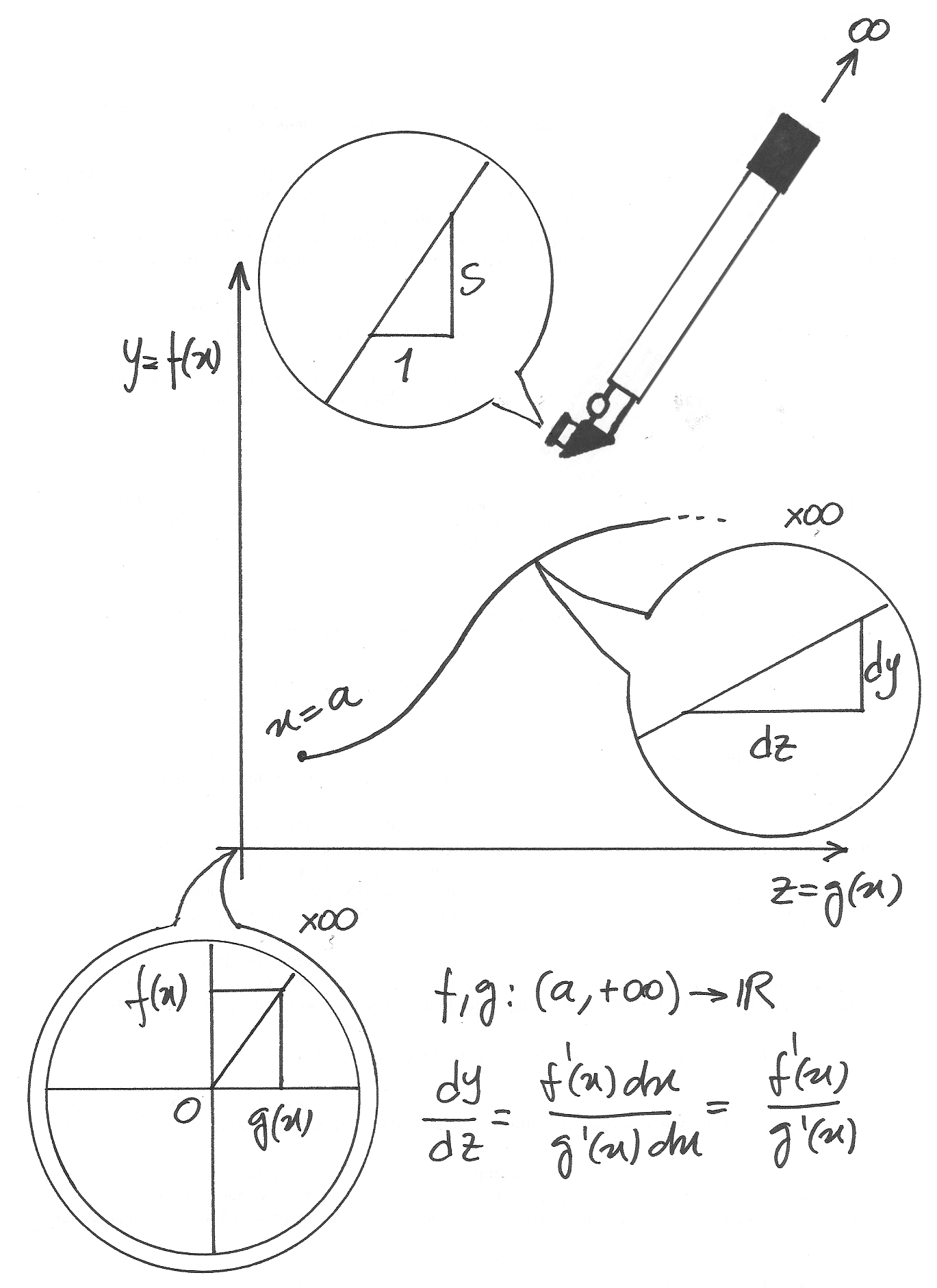
Il caso precedente introduce una regola importante, che permette di valutare, nei casi dubbi, il comportamento asintotico del rapporto fra due funzioni. Nell’illustrare questa regola ci accorgeremo di percorrere ragionamenti simili a quelli visti a proposito del criterio del rapporto fra differenze, nelle successioni.
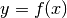 e
e 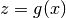 sono due funzioni, definite per esempio su un
intervallo illimitato a destra, con
sono due funzioni, definite per esempio su un
intervallo illimitato a destra, con
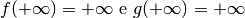 ,
sono entrambe derivabili, con
,
sono entrambe derivabili, con 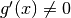 .
Se vale
.
Se vale 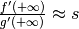 , allora il quoziente
delle funzioni ha lo stesso comportamento asintotico del quoziente delle
derivate, cioè
, allora il quoziente
delle funzioni ha lo stesso comportamento asintotico del quoziente delle
derivate, cioè
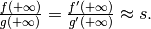
Per ogni valore di  consideriamo le coppie
consideriamo le coppie 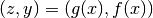 e mettiamo in grafico i punti relativi, con gli
e mettiamo in grafico i punti relativi, con gli  come ascisse: ne
risulterà una certa curva nel piano cartesiano. Il grafico si sviluppa verso destra
perché
come ascisse: ne
risulterà una certa curva nel piano cartesiano. Il grafico si sviluppa verso destra
perché 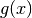 è crescente (la sua derivata è positiva). Si tratta quindi
del grafico di una nuova funzione, che per un certo valore
è crescente (la sua derivata è positiva). Si tratta quindi
del grafico di una nuova funzione, che per un certo valore  avrà pendenza
avrà pendenza
.
Nel disegno, il telescopio visualizza all’infinito che il grafico della curva è
indistinguibile da una semiretta che ha pendenza  .
Osservando l’origine con uno zoom non standard, quindi da una distanza
infinita, si vede la semiretta come se uscisse dall’origine, indistinguibile da
una retta di equazione
.
Osservando l’origine con uno zoom non standard, quindi da una distanza
infinita, si vede la semiretta come se uscisse dall’origine, indistinguibile da
una retta di equazione 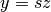 .
Questo determina l’uguaglianza all’infinito fra il rapporto delle funzioni e
il rapporto dei differenziali.
.
Questo determina l’uguaglianza all’infinito fra il rapporto delle funzioni e
il rapporto dei differenziali.
Nel nostro esempio abbiamo supposto 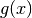 crescente, ma la dimostrazione
vale anche se
crescente, ma la dimostrazione
vale anche se 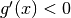 .
.
Si può applicare lo stesso ragionamento anche se le due funzioni convergono a zero quando x diverge all’infinito e anche quando x converge nella monade di un numero standard.
Esempio¶
Studiamo il comportamento asintotico della funzione 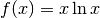 nello zero.
Si tratta di una forma indeterminata perché
nello zero.
Si tratta di una forma indeterminata perché 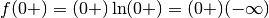 .
Riscriviamo la funzione come un rapporto:
.
Riscriviamo la funzione come un rapporto: 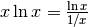 .
In questo modo la forma indeterminata diventa un quoziente fra infiniti.
La derivata del denominatore è
.
In questo modo la forma indeterminata diventa un quoziente fra infiniti.
La derivata del denominatore è 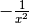 , cioè è sempre negativa e
possiamo applicare la regola di De L’Hôpital per determinare il comportamento
asintotico della funzione:
, cioè è sempre negativa e
possiamo applicare la regola di De L’Hôpital per determinare il comportamento
asintotico della funzione:
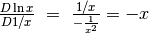 , che diventa infnitesimo
per
, che diventa infnitesimo
per 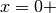 . Quindi
. Quindi 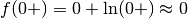
Gli asintoti¶
Una retta è un asintoto per una funzione se i loro due grafici sono indistinguibili
a una distanza infinita dall’origine. Per esempio l’asse y è un asintoto per le
funzioni logaritmiche e la retta 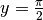 è un asintoto per
l’arcotangente.
è un asintoto per
l’arcotangente.
Quadro dei comportamenti asintotici¶
In sintesi, una funzione a dominio continuo può avere questi comportamenti:
Asintoti verticali, orizzontali, obliqui.¶
Non è detto che una funzione abbia degli asintoti, ma se ne ha possono essere di tre tipi e possono anche essere tutti e tre presenti per la stessa funzione.
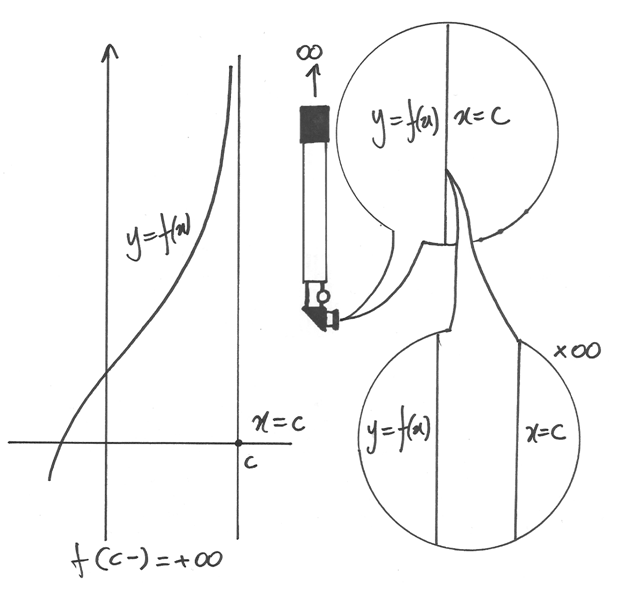
Asintoti verticali¶
Un asintoto verticale è una retta di equazione 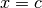 ,
per cui la funzione assume valori infiniti
positivi o negativi se
,
per cui la funzione assume valori infiniti
positivi o negativi se  si avvicina infinitamente a
si avvicina infinitamente a  . Questo
accade per le funzioni logaritmo, per le funzioni tangente e per tutte le
funzioni per le quali è possibile uno dei casi seguenti:
. Questo
accade per le funzioni logaritmo, per le funzioni tangente e per tutte le
funzioni per le quali è possibile uno dei casi seguenti:
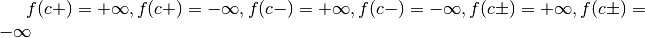 .
.
Una funzione può avere anche infiniti asintoti verticali.
Asintoti orizzontali¶
Gli asintoti orizzontali sono le rette di equazione 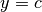 e possono
valere le scritture:
e possono
valere le scritture:
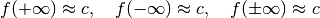 .
.
Il primo caso è un asintoto orizzontale destro (per es. 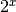 ),
il secondo è un asintoto orizzontale sinistro (per es.
),
il secondo è un asintoto orizzontale sinistro (per es. 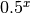 ).
Una funzione può avere anche entrambi i tipi, ma ovviamente non
più di due.
).
Una funzione può avere anche entrambi i tipi, ma ovviamente non
più di due.
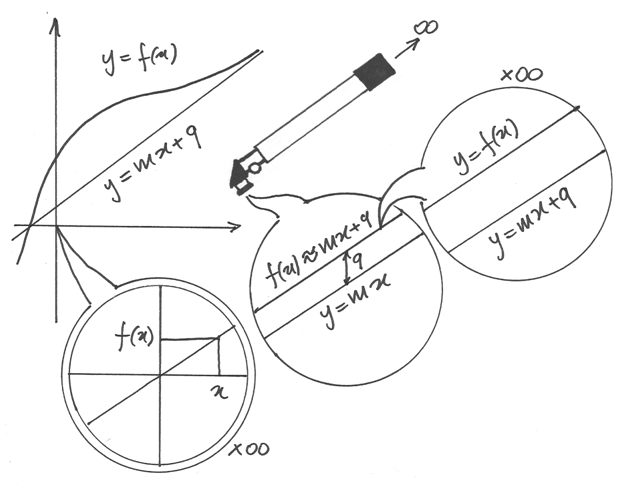
Asintoti obliqui¶
Una retta del tipo 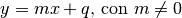 è un asintoto obliquo per
la funzione f(x) se
è un asintoto obliquo per
la funzione f(x) se 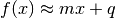 per valori infiniti di x.
L’asintoto obliquo può essere destro, per
per valori infiniti di x.
L’asintoto obliquo può essere destro, per 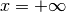 , come nel disegno,
o sinistro
, come nel disegno,
o sinistro 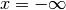 .
.
Il disegno mostra che la retta, osservata nell’origine con lo zoom non standard,
passa per l’origine anche se 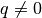 , perché da una distanza infinita
, perché da una distanza infinita
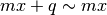 . Se la retta è un asintoto obliquo, per esempio destro,
per
. Se la retta è un asintoto obliquo, per esempio destro,
per 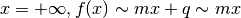 e quindi
e quindi 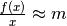 .
All’infinito, la funzione è quindi indistinguibile da due rette: y=mx+q e y=mx .
Le due rette differiscono in ordinata per q e quindi la funzione è
infinitamente vicina alla prima retta e differisce dalla seconda per
.
All’infinito, la funzione è quindi indistinguibile da due rette: y=mx+q e y=mx .
Le due rette differiscono in ordinata per q e quindi la funzione è
infinitamente vicina alla prima retta e differisce dalla seconda per 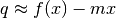 .
.
Quindi l’asintoto obliquo esiste a queste ben precise condizioni. Ovviamente la funzione può andare all’infinito anche senza che vi sia un asintoto obliquo. Se invece troviamo che c’è un asintoto obliquo, non è detto che q sia diverso da zero.
Esempi¶
- Studia il comportamento asintotico di
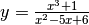 .
.
Il denominatore si scompone in 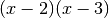 , quindi la funzione non è definita
per
, quindi la funzione non è definita
per 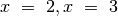 . Studiamo in questi punti il comportamento asintotico.
. Studiamo in questi punti il comportamento asintotico.
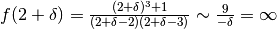 .
.
Quindi la retta 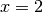 è un asintoto verticale.
Quando
è un asintoto verticale.
Quando  si avvicina a 2 da sinistra cioè
si avvicina a 2 da sinistra cioè 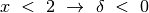 il valore della funzione cresce a
il valore della funzione cresce a 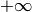 .
Quando
.
Quando  si avvicina a 2 da destra cioè
si avvicina a 2 da destra cioè 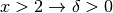 ,
il valore della funzione decresce a
,
il valore della funzione decresce a 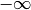 .
.
Vediamo cosa succede per
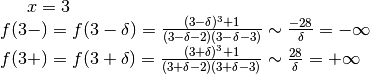 .
.
Quindi anche 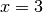 è asintoto verticale, ma questa volta il grafico della
funzione va a
è asintoto verticale, ma questa volta il grafico della
funzione va a 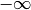 avvicinandosi alla retta da sinistra e va a
avvicinandosi alla retta da sinistra e va a
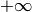 da destra.
da destra.
Vediamo cosa succede agli estremi dell’intervallo: per 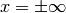 .
.
Poiché 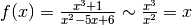 ,
,
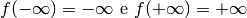 .
Quindi la funzione all’infinito è un infinito.
.
Quindi la funzione all’infinito è un infinito.
Vediamo se nell’andare all’infinito, la funzione ha un asintoto obliquo.
A sinistra:  all’infinito è indistinguibile da una retta di
pendenza
all’infinito è indistinguibile da una retta di
pendenza 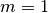 , e quindi di equazione
, e quindi di equazione 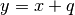 .
Per verificare se
.
Per verificare se 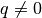 studiamo il comportamento asintotico di
studiamo il comportamento asintotico di
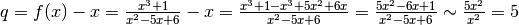 .
.
Quindi l’asintoto sinistro è la retta 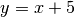 .
Anzi, poiché i calcoli non cambiano nella ricerca di un asintoto destro,
la stessa retta è anche asintoto obliquo destro. Per concludere,
la funzione ha due asintoti verticali e un asintoto obliquo sinistro e destro.
.
Anzi, poiché i calcoli non cambiano nella ricerca di un asintoto destro,
la stessa retta è anche asintoto obliquo destro. Per concludere,
la funzione ha due asintoti verticali e un asintoto obliquo sinistro e destro.
- Studia il comportamento asintotico di
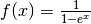 .
.
La funzione non è definita per 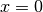 perché
perché 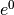 annulla il
denominatore. Quindi studiamo il comportamento asintotico in 0.
annulla il
denominatore. Quindi studiamo il comportamento asintotico in 0.
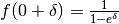 è un infinito negativo se
è un infinito negativo se
 , ma positivo se
, ma positivo se  .
Infatti
.
Infatti 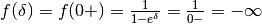 e
e
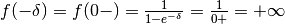 .
.
Se  è un infinito:
è un infinito:
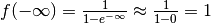 e
e
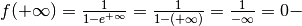 Quindi l’asse x è un asintoto orizzontale destro, mentre la retta
Quindi l’asse x è un asintoto orizzontale destro, mentre la retta 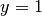 è un asintoto orizzontale sinistro.
Per concludere ci sono due asintoti orizzontali ed uno verticale.
è un asintoto orizzontale sinistro.
Per concludere ci sono due asintoti orizzontali ed uno verticale.
- Studia il comportamento asintotico in zero di
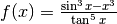 .
.
Il numeratore e il denominatore diventano infinitesimi per 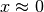 ,
quindi la funzione diventa una forma indeterminata, che proviamo a risolvere
applicando la regola di De l’Hôpital.
,
quindi la funzione diventa una forma indeterminata, che proviamo a risolvere
applicando la regola di De l’Hôpital.
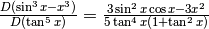 .
È ancora il quoziente di due infinitesimi, con espressioni più
complicate. Rinunciamo a sviluppare di nuovo la stessa regola e riprendiamo da
capo, trasformando la funzione.
.
È ancora il quoziente di due infinitesimi, con espressioni più
complicate. Rinunciamo a sviluppare di nuovo la stessa regola e riprendiamo da
capo, trasformando la funzione.
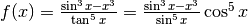 .
Il vantaggio è che per
.
Il vantaggio è che per  infinitesimo
infinitesimo 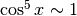 ,
quindi possiamo studiare il comportamento asintotico solo di
,
quindi possiamo studiare il comportamento asintotico solo di
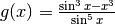 .
Trattandosi del rapporto fra due infinitesimi, applichiamo l’Hôpital e così facciamo
ogni volta che il risultato ottenuto è un rapporto fra infinitesimi
(il simbolo
.
Trattandosi del rapporto fra due infinitesimi, applichiamo l’Hôpital e così facciamo
ogni volta che il risultato ottenuto è un rapporto fra infinitesimi
(il simbolo 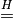 indica che si è usata la regola di de l’Hôpital):
indica che si è usata la regola di de l’Hôpital):
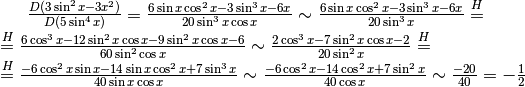
Nello sviluppare i denominatori abbiamo sempre tenuto conto che
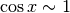 e per questo abbiamo inserito il simbolo di
e per questo abbiamo inserito il simbolo di
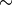 al posto =.
In conclusione, la funzione assume valori sempre più prossimi a
al posto =.
In conclusione, la funzione assume valori sempre più prossimi a
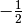 per
per  sempre più prossimo a zero.
sempre più prossimo a zero.
Note
Nell’applicare la regola di de l’Hôpital alla funzione 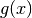 avremmo potuto scegliere anche una strada sbagliata:
avremmo potuto scegliere anche una strada sbagliata:
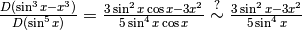 ,
dato che
,
dato che 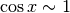 .
.
Si tratta ancora di una forma indeterminata, alla quale applichiamo di nuovo la stessa regola.
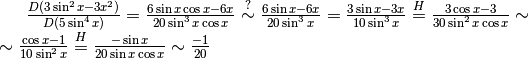
Il risultato è ottenuto applicando ripetutamente l’Hôpital e valutando che
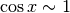 per x infinitesimo.
L’errore sta nell’applicare questa valutazione anche nel punto sbagliato
(che è segnato con ”?”), cioè al numeratore all’interno di una differenza.
In quel punto il contributo di
per x infinitesimo.
L’errore sta nell’applicare questa valutazione anche nel punto sbagliato
(che è segnato con ”?”), cioè al numeratore all’interno di una differenza.
In quel punto il contributo di 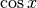 non può essere eliminato,
come non può esserlo all’inizio della seconda riga.
Un fattore asintoticamente indistinguibile da 1 può essere trascurato solo
se moltiplica o divide tutta l’espressione, come avviene
nell’individuare g(x) e per tutti i denominatori dell’esercizio.
non può essere eliminato,
come non può esserlo all’inizio della seconda riga.
Un fattore asintoticamente indistinguibile da 1 può essere trascurato solo
se moltiplica o divide tutta l’espressione, come avviene
nell’individuare g(x) e per tutti i denominatori dell’esercizio.
Per chiarire, studiamo in zero il comportamento asintotico di
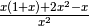 .
Considerando
.
Considerando 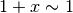 , la somma al numeratore si riduce e la
frazione poi si semplifica, risultando infinitamente vicina a 2.
Se invece si svolgono con pazienza tutti i calcoli algebrici, al termine
delle semplificazioni, la frazione risulta uguale a 3 ed è il risultato
corretto.
La valutazione
, la somma al numeratore si riduce e la
frazione poi si semplifica, risultando infinitamente vicina a 2.
Se invece si svolgono con pazienza tutti i calcoli algebrici, al termine
delle semplificazioni, la frazione risulta uguale a 3 ed è il risultato
corretto.
La valutazione 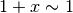 non va fatta in quel contesto perché
con quella sostituzione si provoca la scomparsa di termini di secondo grado
che sono gli unici ad influire sulla somma algebrica, dato che che quelli
di primo grado si eliminano algebricamente.
non va fatta in quel contesto perché
con quella sostituzione si provoca la scomparsa di termini di secondo grado
che sono gli unici ad influire sulla somma algebrica, dato che che quelli
di primo grado si eliminano algebricamente.
Note
La regola di de l’Hôpital è di grande aiuto nell’abbassare il grado delle funzioni polinomiali, mentre diventa una complicazione in molti altri casi. Per questi occorre uno strumento più potente, cioè la regola di Taylor che si vedrà più avanti.
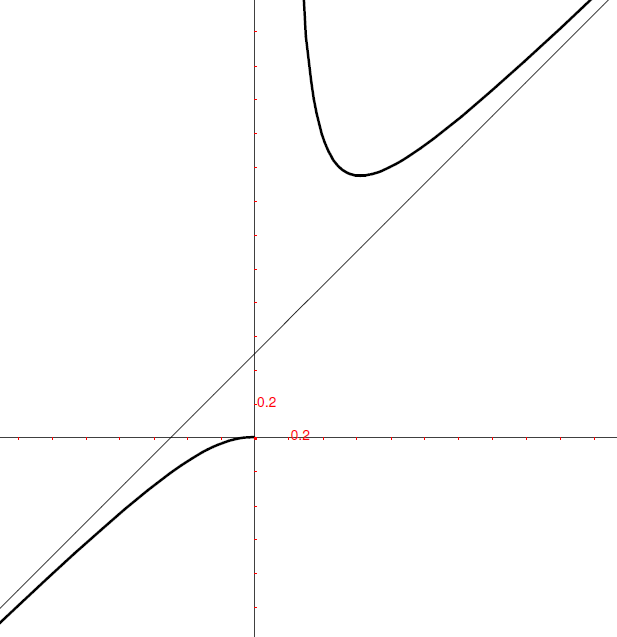
- Studia il comportamento asintotico di
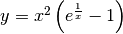
La funzione è definita per ogni 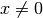 . In
. In 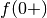 la
funzione assume la forma indeterminata
la
funzione assume la forma indeterminata 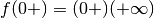 . Per usare
la regola di de l’Hôpital riscriviamo l’espressione della funzione e operiamo la
sostituzione
. Per usare
la regola di de l’Hôpital riscriviamo l’espressione della funzione e operiamo la
sostituzione 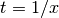 :
:
.
Per 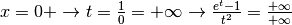 .
Applicando due volte la regola di de l’Hôpital, la forma indeterminata diventa
.
Applicando due volte la regola di de l’Hôpital, la forma indeterminata diventa
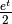 , che è un infinito positivo. Dunque
, che è un infinito positivo. Dunque 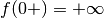 ,
cioè l’asse y è un asintoto verticale.
Invece
,
cioè l’asse y è un asintoto verticale.
Invece 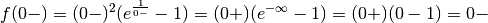 .
Quindi il ramo sinistro della funzione si annulla per valori negativi quando x
si approssima allo zero da sinistra, invece il ramo destro ha un asintoto verticale
nell’asse y.
.
Quindi il ramo sinistro della funzione si annulla per valori negativi quando x
si approssima allo zero da sinistra, invece il ramo destro ha un asintoto verticale
nell’asse y.
Per valori infiniti di x usando la stessa sostituzione si ha 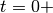 e
la funzione diventa
e
la funzione diventa
che è una forma indeterminata, da risolvere con l’aiuto della regola di de l’Hôpital:
.
Per 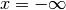 , se si usa la stessa procedura, sia ha
, se si usa la stessa procedura, sia ha 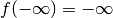 . Quindi la funzione va all’infinito, agli estremi dell’intervallo di definizione.
. Quindi la funzione va all’infinito, agli estremi dell’intervallo di definizione.
Occorre ora verificare l’esistenza di eventuali asintoti obliqui.
Per 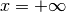 :
:
,
dove si utilizza la solita regola in presenza di un rapporto fra due infinitesimi. Quindi l’asintoto obliquo esiste a destra ed ha pendenza 1. Per ricavare q:
che è ancora una forma indeterminata.
Interveniamo con la regola di de l’Hôpital e otteniamo:
.
La retta che funge da asintoto è quindi 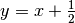 e si può verificare
che il risultato vale sia per l’asintoto obliquo destro che per quello sinistro.
e si può verificare
che il risultato vale sia per l’asintoto obliquo destro che per quello sinistro.
In conclusione la funzione ha un asintoto verticale e un asintoto obliquo sia destro che sinistro.
Il grafico riprende il disegno precedente, guardando l’origine con lo zoom che ingrandisce 250 volte. Si vede così che l’asintoto, osservato da grande distanza, sembra passare per l’origine: si mantiene il coefficiente angolare e si annulla l’intercetta all’origine, come illustrato nel 15.5.3.
Osservazione banale ma importante¶
La regola di de l’Hôpital si applica al rapporto fra due funzioni, ma è diversa dalla regola di derivazione del rapporto.
Confronta con attenzione le due regole:
de l’Hôpital: nei casi di indecisione e a determinate condizioni: comportamento asintotico di
= comportamento asintotico di
.
Derivata:
.
Riassunto¶
- Le successioni possono avere all’infinito un comportamento regolare o irregolare. Una successione che all’infinito si avvicina ad un certo valore
 , si dice che converge a
, si dice che converge a  oppure che
oppure che  è il suo asintoto. Una successione che all’infinito raggiunge valori infiniti, si dice che diverge (positivamente o negativamente), oppure che diverge asintoticamente. Questi sono i comportamenti regolari.
è il suo asintoto. Una successione che all’infinito raggiunge valori infiniti, si dice che diverge (positivamente o negativamente), oppure che diverge asintoticamente. Questi sono i comportamenti regolari. - Illustriamo 5 criteri che aiutano a stabilire se una successione ha un comportamento regolare e quale sia. Si costruisce così una gerarchia di comportamenti asintotici:
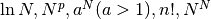 è la scala degli infiniti, in ordine crescente.
è la scala degli infiniti, in ordine crescente. - Un asintoto per una funzione è una retta alla quale il grafico della funzione si avvicina indefinitamente. Studiare il comportamento asintotico di una funzione significa cercare se quella retta esiste quando la x si pone agli estremi dell’intervallo di definizione.
- Vi sono asintoti orizzontali, verticali e obliqui e una funzione può averli tutti, oppure alcuni o nessuno. La casistica è riportata nel paragrafo 13.4.1.
- Nel ricercare l’asintoto si ha spesso a che fare con i casi di indeterminazione. Per risolvere le forme indeterminate viene in aiuto la regola di de l’Hôpital, che assicura, solo se sono verificate determinate condizioni, che il rapporto fra due funzioni ha lo stesso comportamento asintotico del rapporto fra le loro derivate.
Esercizi¶
- Calcolando i rapporti opportuni, dimostra la gerarchia dei comportamenti asintotici per le successioni. In particolare dimostra che il rapporto fra
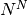 e
e 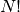 è asintotico al Numero di Nepero.
è asintotico al Numero di Nepero. - Applica il criterio della radice al rapporto già noto
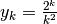
- Descrivi il comportamento della funzione
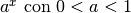 , usando i termini specifici introdotti all’inizio del capitolo.
, usando i termini specifici introdotti all’inizio del capitolo. - Spiega perché la tangente ha un comportamento asintotico irregolare per x che diverge.
- Svolgi autonomamente gli esercizi svolti negli esempi, ricavando anche i risultati che il testo sottointende.



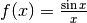
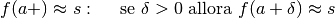
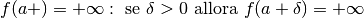
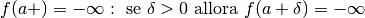
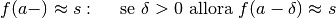
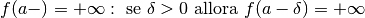
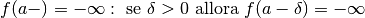
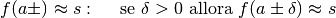
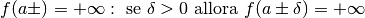
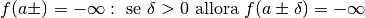
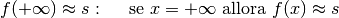
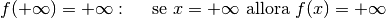
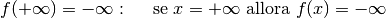
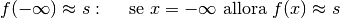
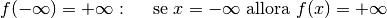
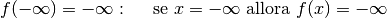
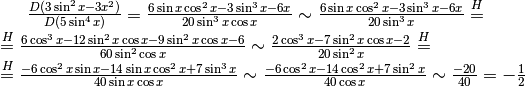
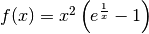 .
.