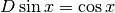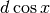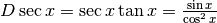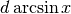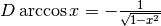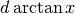La derivata delle funzioni circolari e delle loro inverse¶

Per giustificare le formule delle derivate di funzioni circolari e delle loro inverse, faremo ampio uso dei microscopi, che rendono i risultati più immediati ed evidenti di quanto non faccia il calcolo. Useremo il calcolo soprattutto per confermare i risultati già trovati.

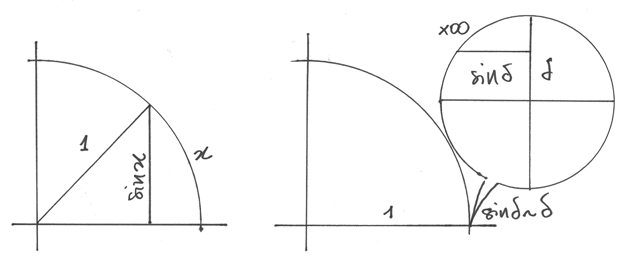
Derivare y=sin x¶

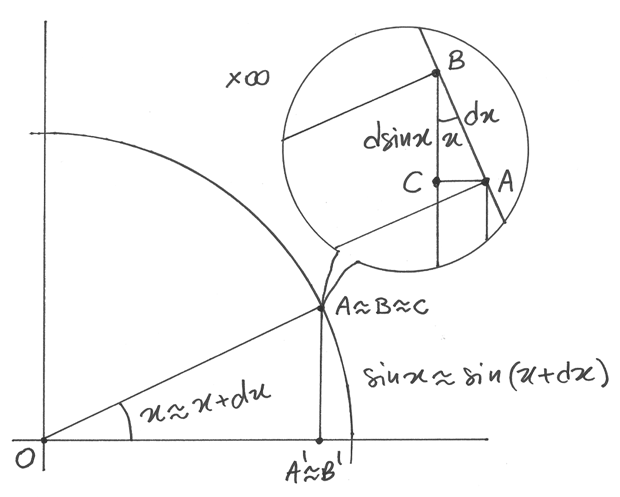
Un arco di circonferenza, ingrandito al microscopio non standard, è indistinguibile da un segmento. Quindi per ogni 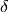$\delta$ infinitesimo non nullo, si ha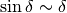 $\sin \delta \sim \delta$

$\sin \delta \sim \delta$

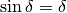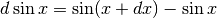Per le convenzioni già discusse nel capitolo precedente, potremo scrivere $\sin \delta =\delta$ . Cerchiamo ora di esprimere la differenza $d\sin x=\sin (x+dx)-\sin x$ .

L’incremento infinitesimo di angolo dx è racchiuso fra i due raggi OA e OB, che sono indistinguibili da segmenti paralleli, e l’arco AB corrisponde all’angolo dx ed è indistinguibile da un segmento rettilineo. Nell’ingrandimento al microscopio non standard AA’ e BB’ sono segmenti distinti paralleli, e C è la proiezione di A su BB’. 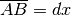Allora il triangolo curvilineo ABC è indistinguibile da un triangolo rettangolo e AC è l’incremento infinitesimo di sin x, relativo all’incremento $\overline{AB} = dx$ . 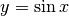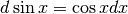$y=\sin x$ è una funzione continua, perché associa all’incremento infinitesimo dx l’incremento infinitesimo $d\sin x$ , dato da: $d\sin x=\cos x dx$ . Per cui, come già si intuiva osservando l’andamento delle tangenti di una sinusoide, la derivata risulta:

$D\sin x= \cos x$

Volendo dimostrare tutto questo con il calcolo, dobbiamo ricorrere alle espressioni per le differenze del cap.5, che sono:

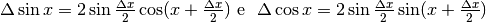
$\Delta\sin x=2\sin\frac{\Delta x}{2}\cos (x+\frac{\Delta x}{2})\mbox{ e }\ \Delta \cos x= 2\sin\frac{\Delta x}{2}\sin (x+\frac{\Delta x}{2})$

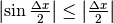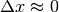Prima di sostituire le differenze con i differenziali, dobbiamo accertarci che le due funzioni siano continue. Poiché il seno è una corda e quindi è minore dell’arco ( $\left|\sin\frac{\Delta x}{2}\right|\le\left|\frac{\Delta x}{2}\right|$ ) e poichè il coseno è sempre minore di 1, o al massimo uguale, se $\Delta x \approx 0$ ,

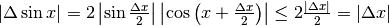$\left |\Delta\sin x\right |=2\left |\sin\frac{\Delta x}{2}\right |\left |\cos \left(x+\frac{\Delta x}{2}\right)\right |\le 2\frac{\left |\Delta x\right |}{2}=\left |\Delta x\right |$ .

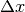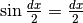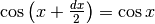Allora $\Delta \sin x$ è infinitesimo per $\Delta x$ infinitesimo, quindi la funzione seno è continua. Per la funzione coseno il procedimento è simile, per cui possiamo scrivere: $\sin\frac{dx}{2}=\frac{dx}{2}$ e $\\ \cos\left(x+\frac{dx}{2} \right)=\cos x$ e infine, passando dalle differenze ai differenziali si perviene alla formula già vista:

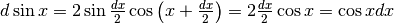$d\sin x=2\sin\frac{dx}{2}\cos\left(x+\frac{dx}{2}\right)=2\frac{dx}{2}\cos x=\cos x dx$ .

Come si nota, la dimostrazione attraverso il calcolo è molto meno intuitiva. Nel seguito ne faremo uso solo se strettamente indispensabile.

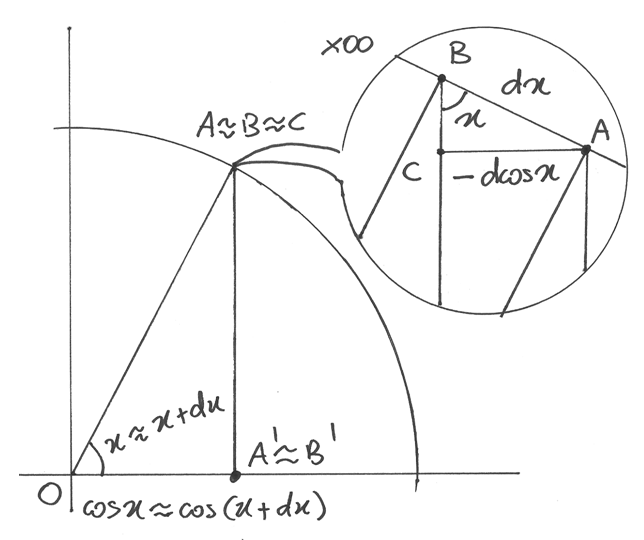
Derivare y=cos x¶

$d\cos x$

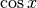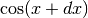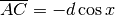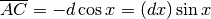In questo disegno OB’ rappresenta $\cos x$ e OA’ rappresenta $\cos (x+dx)$ . Ingrandito al microscopio non standard, abbiamo $\overline{AC}=-d\cos x$ , con il segno negativo perché al crescere dell’arco il coseno diminuisce. ABC è un triangolo rettangolo con l’ipotenusa dx e l’angolo in B uguale ad x. Allora $\overline{AC}=-d\cos x=(dx)\sin x$ , da cui si ricava che 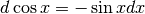$d\cos x=-\sin x dx$ . Da qui la regola di derivazione:

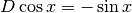$D\cos x=-\sin x$ .

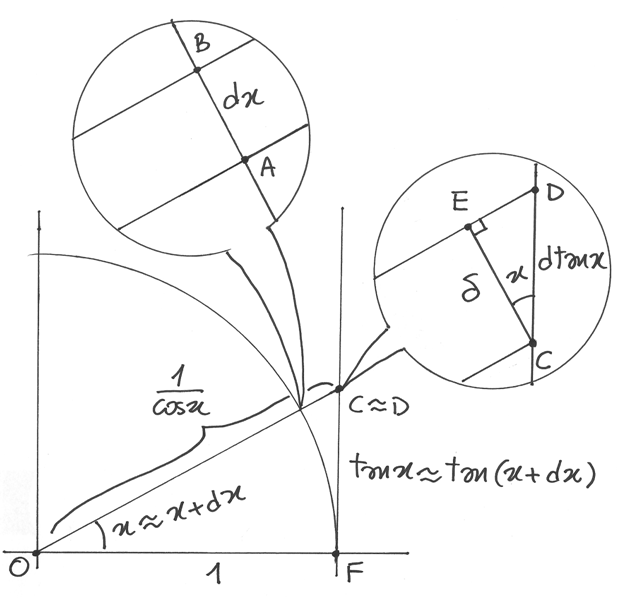
Derivare y=tan x¶

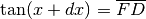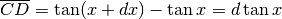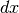Nel cerchio goniometrico, la tangente $\tan x$ è il segmento FC, mentre $\tan (x+dx)=\overline{FD}$ , sicché $\overline{CD}=\tan (x+dx)-\tan x= d\tan x$ . In corrispondenza di CD abbiamo l’arco AB , relativo all’incremento $dx$ dell’angolo x.

$d\tan x$

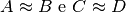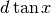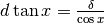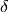Con due microscopi non standard, regolati allo stesso ingrandimento, visualizziamo i punti infinitamente vicini $A \approx B \mbox{ e } C \approx D$ . I raggi per A e per B si vedranno paralleli e potremo disegnare il segmento CE parallelo ad AB, in modo che CED sia un triangolo rettangolo di ipotenusa $d\tan x$ . Ne risulta che $d\tan x=\frac{\delta}{\cos x}$ . 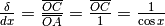Per ricavare $\delta$ , vediamo che il triangolo isoscele OAB è simile a OCE e quindi vale $\frac{\delta}{dx}=\frac{\overline{OC}}{\overline{OA}}=\frac{\overline{OC}}{1}=\frac{1}{\cos x}$ . 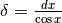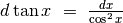Allora $\delta=\frac{dx}{\cos x}$ e $d\tan x~=~\frac{dx}{\cos^2 x}$ . 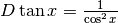Se ne conclude che: $D\tan x=\frac{1}{\cos^2 x}$ .

Si perviene allo stesso risultato in modo tortuoso attraverso il calcolo e, in modo più interessante, usando la regola della derivata di un quoziente, applicata a 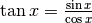$\tan x = \frac{\sin x}{\cos x}$ , che porta anche a un risultato equivalente: 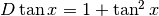$D\tan x = 1 + \tan^2 x$ . In conclusione:

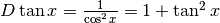$D\tan x=\frac{1}{\cos^2 x}= 1 +\tan^2 x$ .

Con la regola della derivata di un rapporto si ricavano anche le regole delle derivate delle funzioni cotangente, secante, cosecante. Dimostriamo per via geometrica solo uno di questi casi, riportando poi in sintesi tutti i risultati al termine del capitolo.

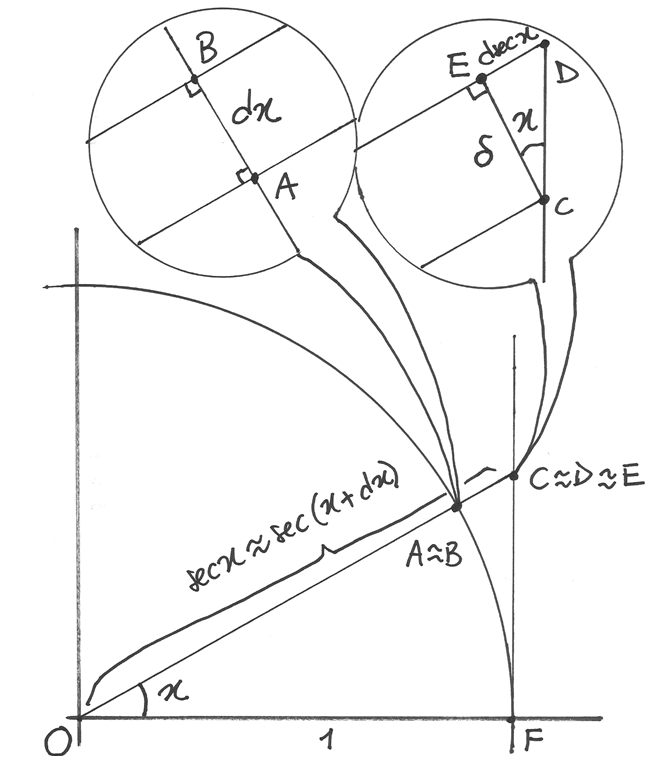
Derivare y=sec x¶

Il disegno è analogo a quello del caso precedente. Questa volta cerchiamo l’espressione di: 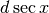$d\sec x$ che nel disegno corrisponde al segmento DE .

$d\sec x$

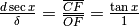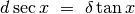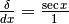Per la similitudine dei triangoli CED e COF abbiamo: $\frac{d\sec x}{\delta}=\frac{\overline{CF}}{\overline{OF}}=\frac{\tan x}{1}$ . Da cui $d\sec x~=~\delta\tan x$ . Ma sono simili anche i triangoli isosceli OAB e OCE, da cui $\frac{\delta}{dx}=\frac{\sec x}{1}$ . Ricavando 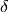$\delta$ e sostituendo nella precedente, si ha infine: 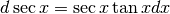$d \sec x=\sec x \tan x dx$ . La derivata è quindi:

$D\sec x=\sec x\tan x=\frac{\sin x}{\cos^2 x}$

La seconda espressione si ottiene per semplici trasformazioni goniometriche.

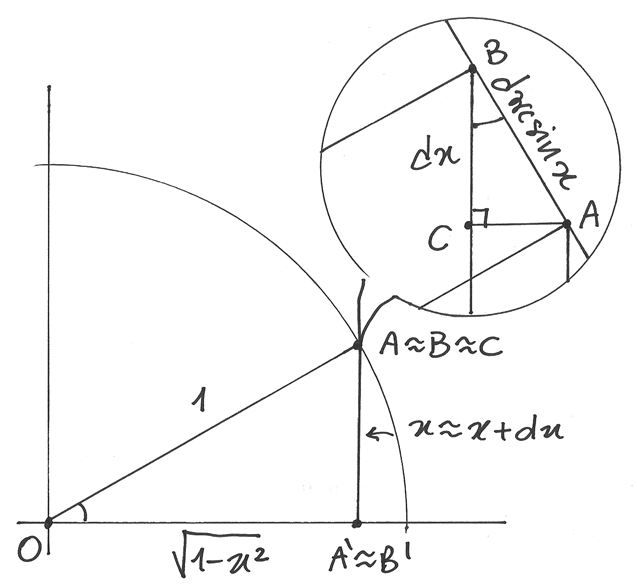
Derivare y=arcsin x¶

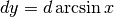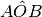Nel prossimo disegno, x è il seno dell’angolo $y=\arcsin x$ . Quindi dx è l’incremento della funzione seno, corrispondente all’incremento infinitesimo dell’angolo $dy=d\arcsin x$ , cioé $A\hat{O}B$ .

$d\arcsin x$

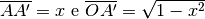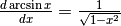A’ e B’ sono le proiezioni di A e di B sull’asse orizzontale, quindi $\overline{AA'}=x \mbox{ e } \overline{OA'}=\sqrt{1-x^2}$ . C è la proiezione di A su BB’ e forma così un triangolo rettangolo ABC simile a AOA’. Dalla similitudine si ricava che $\frac{d\arcsin x}{dx}=\frac{1}{\sqrt{1-x^2}}$ , da cui deriva la regola di derivazione:

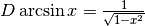$D\arcsin x=\frac{1}{\sqrt{1-x^2}}$ .

Questa derivata non è definita per 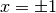$x=\pm 1$ e infatti per questi valori di x la funzione arcoseno ha tangente verticale.

Derivare y=arccos x¶

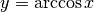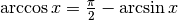La derivata della funzione $y=\arccos x$ si ottiene attraverso considerazioni analoghe alle precedenti. Si può avere la conferma del risultato dal fatto che la somma $\arcsin x +\arccos x= \frac{\pi}{2}$ . Allora: $\arccos x = \frac{\pi}{2}-\arcsin x$ e quindi

$D\arccos x=-\frac{1}{\sqrt{1-x^2}}$

dato che la derivata di una costante è nulla.

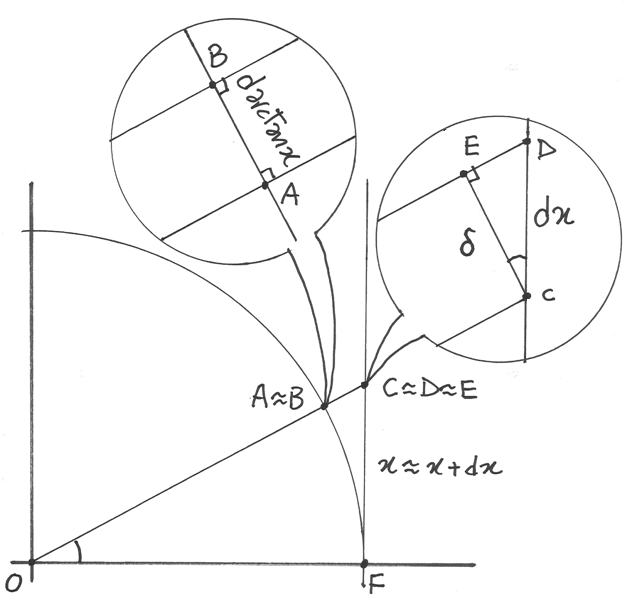
Derivare y=arctan x¶

$d\arctan x$

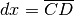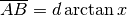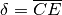Nel disegno, $dx=\overline{CD}$ è l’incremento infinitesimo nel valore della tangente, relativo all’incremento infinitesimo di arco $\overline{AB}=d\arctan x$ . Posizionati i due microscopi non standard come al solito, chiamiamo E la proiezione di C sul raggio prolungato OD e chiamiamo $\delta=\overline{CE}$ . Avremo così un triangolo rettangolo DCE simile al triangolo COF. Dalla similitudine si ricava la relazione: 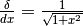$\frac{\delta}{dx}=\frac{1}{\sqrt{1+x^2}}$ . 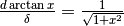Come nei casi precedenti, individuiamo altri due triangoli simili: AOB e BOC, il che ci porta a dedurre: $\frac{d\arctan x}{\delta}=\frac{1}{\sqrt{1+x^2}}$ . 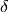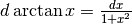Ricavando $\delta$ dalla prima relazione e sostituendolo nella seconda, si ha il differenziale: $d\arctan x= \frac{dx}{1+x^2}$ , e la derivata:

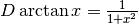$D\arctan x= \frac{1}{1+x^2}$ .

Derivare y=arccot x¶

Anche per questa derivata si può ricavare l’espressione seguendo il ragionamento fatto a proposito dell’arcocoseno. Si avrà facilmente:

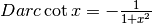$Darc\cot x = -\frac{1}{1+x^2}$ .

Riassumendo¶

Abbiamo ricavato principalmente per via geometrica le formule dei differerenziali e delle derivate delle funzioni goniometriche e delle loro inverse.

y	dy	y’
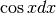$\sin x$	$\cos x dx$	$\cos x$
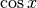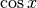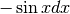$\cos x$	$-\sin x dx$	$-\sin x$
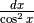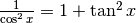$\tan x$	$\frac{dx}{\cos^2 x}$	$\frac{1}{\cos^2 x}= 1 +\tan^2 x$
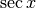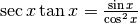$\sec x$	$\sec x\tan x dx$	$\sec x\tan x=\frac{\sin x}{\cos^2 x}$
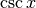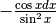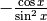$\csc x$	$-\frac{\cos x dx}{\sin^2 x}$	$-\frac{\cos x}{\sin^2 x}$
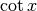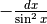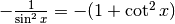$\cot x$	$-\frac{dx}{\sin^2 x}$	$-\frac{1}{\sin^2 x}=-(1+\cot^2 x)$
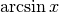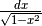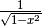$\arcsin x$	$\frac{dx}{\sqrt{1-x^2}}$	$\frac{1}{\sqrt{1-x^2}}$
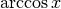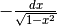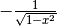$\arccos x$	$-\frac{dx}{\sqrt{1-x^2}}$	$-\frac{1}{\sqrt{1-x^2}}$
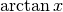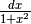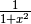$\arctan x$	$\frac{dx}{1+x^2}$	$\frac{1}{1+x^2}$
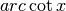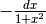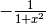$arc\cot x$	$-\frac{dx}{1+x^2}$	$-\frac{1}{1+x^2}$

Esercizi¶

Analizza le tangenti alla cosinusoide e descrivi il loro andamento.
Deduci l’espressione della derivata della tangente usando la regola della derivata del quoziente fra seno e coseno.
Deduci le espressioni delle derivate della cotangente, della secante, della cosecante, utilzzando la regola della derivata del quozionte.