I differenziali, le differenze e i problemi¶
Quale tipologia di problema¶
Nel Cap.5 abbiamo risolto alcuni problemi con il calcolo delle differenze. Si
tratta di problemi nei quali si chiede quale incremento 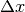 può provocare
nella funzione y un certo incremento dato
può provocare
nella funzione y un certo incremento dato 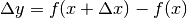 .
Abbiamo già avvisato che si tratta di problemi in generale tutt’altro che semplici,
perchè non è detto che sia possibile trovare un’espressione risolutiva esplicita.
.
Abbiamo già avvisato che si tratta di problemi in generale tutt’altro che semplici,
perchè non è detto che sia possibile trovare un’espressione risolutiva esplicita.
Si cerca allora di superare le difficoltà con gli incrementi infinitesimi
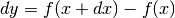 , perché già sappiamo che
, perché già sappiamo che 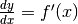 e quindi
e quindi
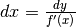 fornisce il valore dell’incognita cercata. Ma quali
difficoltà comporta utilizzare gli incrementi infinitesimi rispetto agli incrementi
finiti e quali relazioni legano gli uni agli altri?
fornisce il valore dell’incognita cercata. Ma quali
difficoltà comporta utilizzare gli incrementi infinitesimi rispetto agli incrementi
finiti e quali relazioni legano gli uni agli altri?
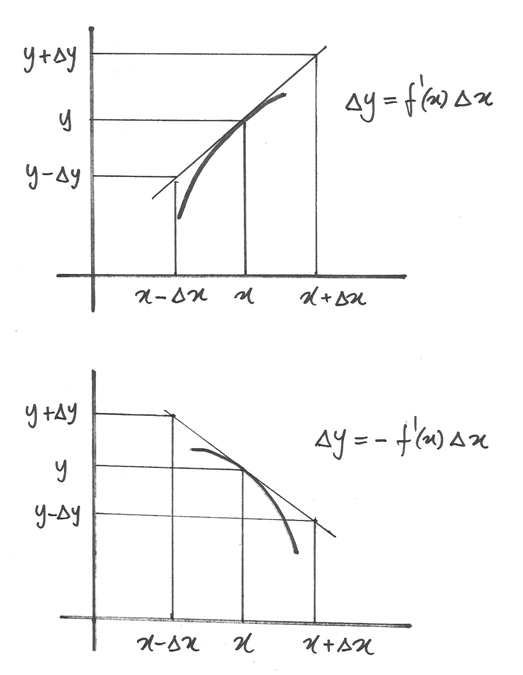
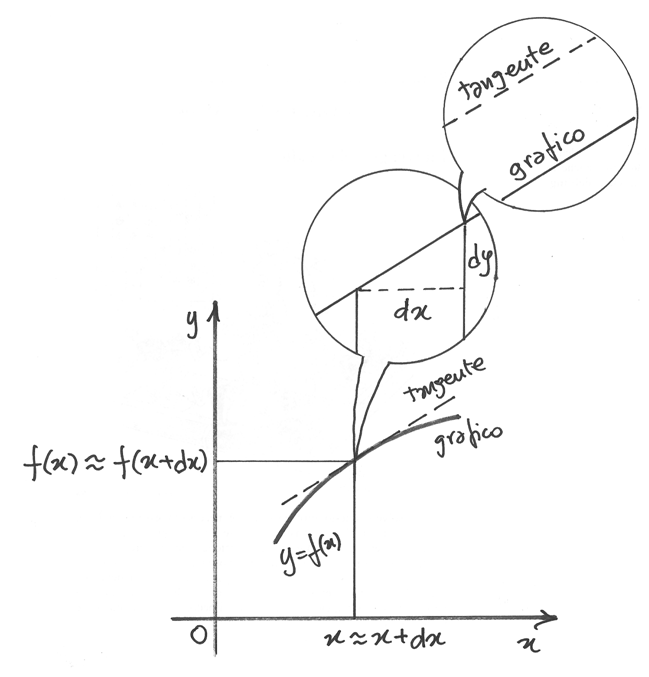
Differenze e differenziali¶
Al microscopio non standard, il grafico della funzione nel punto di ascissa x
appare indistinguibile da un segmento inclinato con pendenza 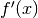 .
Ma sappiamo che indistinguibile non vuol dire esattamente coincidente e inoltre
è una comoda convenzione dire che
.
Ma sappiamo che indistinguibile non vuol dire esattamente coincidente e inoltre
è una comoda convenzione dire che 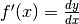 , perché
l’uguaglianza esatta si limita alla parte standard del rapporto differenziale.
Per essere precisi si dovrebbe scrivere
, perché
l’uguaglianza esatta si limita alla parte standard del rapporto differenziale.
Per essere precisi si dovrebbe scrivere 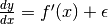 ,
dove
,
dove  è la parte infinitesima.
Allora si ricava
è la parte infinitesima.
Allora si ricava 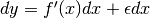 , dove l’ultimo termine è un
infinitesimo di ordine superiore a dx.
Affrontando un problema come quelli descritti, se utilizziamo
, dove l’ultimo termine è un
infinitesimo di ordine superiore a dx.
Affrontando un problema come quelli descritti, se utilizziamo
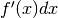 al posto di
al posto di 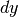 , commettiamo un errore che è infinitesimo
di ordine superiore a dx.
, commettiamo un errore che è infinitesimo
di ordine superiore a dx.
L’errore è ancora maggiore, in generale non infinitesimo, se utilizziamo
incrementi standard 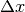 , e tuttavia è un errore contenuto, pensando
, e tuttavia è un errore contenuto, pensando
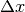 sufficientemente piccolo.
sufficientemente piccolo.
Così, non riuscendo a risolvere il problema con l’equazione corretta
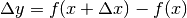 , che esprime l’incremento della funzione,
ci accontentiamo di:
, che esprime l’incremento della funzione,
ci accontentiamo di:
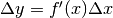
che esprime l’incremento della tangente, pur sapendo che la formula comporta un
errore.
Il vantaggio è che così è facile calcolare l’espressione risolutiva:
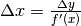 .
.
Applichiamo questa nuova strategia risolutiva agli esempi già visti (Problemi 1 e 2) e cerchiamo di valutare l’errore che comporta l’uso di quest’ultima espressione rispetto alla soluzione esatta. Infine applichiamo la formula approssimata a due problemi nuovi.
Problema 1: La corona circolare¶
Un cerchio ha il raggio di 5 cm. Di quanto deve aumentare il raggio perché l’area
del cerchio aumenti di 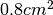 ?
?
L’area è 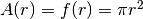 , che ha per derivata
, che ha per derivata 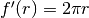 .
.
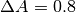 . La formula risolutiva dà:
. La formula risolutiva dà:
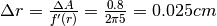 .
.
Questo problema è stato illustrato nel Cap.5 e la soluzione, ricavata con il calcolo del rapporto incrementale, era: 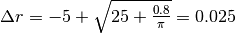 .
La formula dava la soluzione esatta, ma nel risultato avevamo tagliato i decimali.
Ricalcoliamo entrambi i risultati con la calcolatrice e abbiamo:
Soluzione esatta: 0.025400. Soluzione approssimata: 0.025465
Quindi l’approssimazione è molto buona. In più si consideri l’immediatezza della
formula risolutiva approssimata che oltretutto non ha alternativa nei casi in cui
non sia possibile esprimere una formula risolutiva esatta.
.
La formula dava la soluzione esatta, ma nel risultato avevamo tagliato i decimali.
Ricalcoliamo entrambi i risultati con la calcolatrice e abbiamo:
Soluzione esatta: 0.025400. Soluzione approssimata: 0.025465
Quindi l’approssimazione è molto buona. In più si consideri l’immediatezza della
formula risolutiva approssimata che oltretutto non ha alternativa nei casi in cui
non sia possibile esprimere una formula risolutiva esatta.
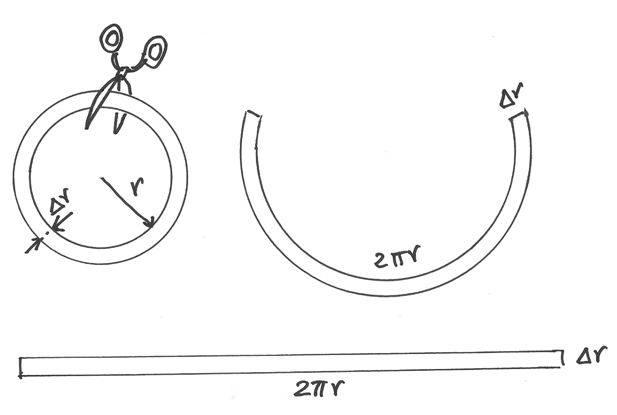
La formula approssimata 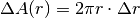 esprime anche un
significato geometrico: si può pensare che la sottile corona circolare che rapprenta
l’area aggiunta sia deformabile e corrisponda all’area di un rettangolo con la base
pari alla circonferenza
esprime anche un
significato geometrico: si può pensare che la sottile corona circolare che rapprenta
l’area aggiunta sia deformabile e corrisponda all’area di un rettangolo con la base
pari alla circonferenza 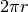 e l’altezza
e l’altezza 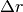 .
.
Problema 2: Il triangolo¶
Riproponiamo anche questo secondo problema, del quale nel Cap.5 abbiamo già esaminato la formula risolutiva esatta.
Un triangolo di lati a, b rispettivamente uguali a 5 e 8 cm e angolo compreso di 40°, subisce un incremento di area di 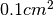 .
Quale incremento di angolo
.
Quale incremento di angolo 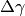 provoca tale incremento di area?
provoca tale incremento di area?
L’area si ricava da: 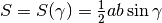 . Poiché il suo
incremento è picccolo, utilizziamo la formula approssimata
. Poiché il suo
incremento è picccolo, utilizziamo la formula approssimata
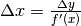 che nel nostro caso diventa:
che nel nostro caso diventa:
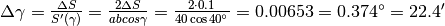 .
.
Nel Cap.5 la formula risolutiva esatta era:
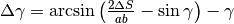 che portava al risultato di
che portava al risultato di 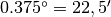 . La formula approssimata
è dunque più semplice e porta ad una errore minimo, di circa una parte su 400.
. La formula approssimata
è dunque più semplice e porta ad una errore minimo, di circa una parte su 400.
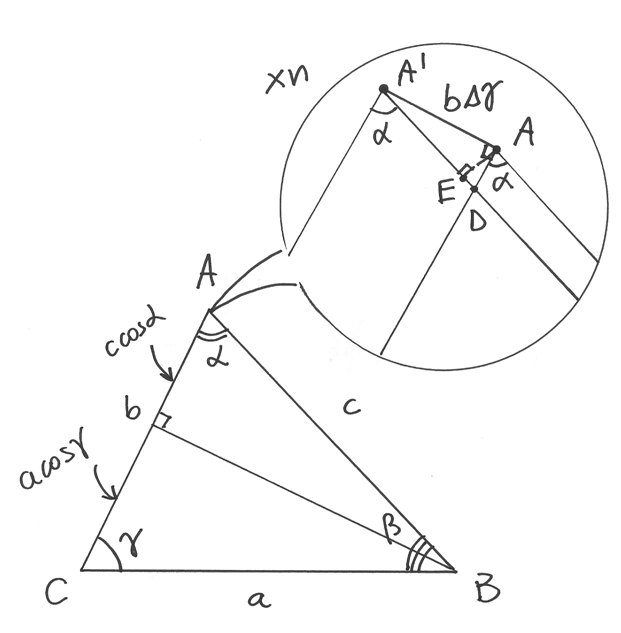
Supponiamo di non conoscere le derivate e quindi nemmeno la formula approssimata
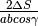 . Attraverso quali considerazioni geometriche
possiamo ricavarla? Dobbiamo puntare in A un microscopio standard (l’incremento
. Attraverso quali considerazioni geometriche
possiamo ricavarla? Dobbiamo puntare in A un microscopio standard (l’incremento
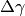 è piccolo, non infinitesimo) e visualizzare il nuovo vertice A’
che si ottiene dopo avere incrementato
è piccolo, non infinitesimo) e visualizzare il nuovo vertice A’
che si ottiene dopo avere incrementato 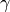 . Il segmento BA’ riduce l’area
del triangolo iniziale, mentre il segmento CA’ la aumenta. Quindi l’incremento
. Il segmento BA’ riduce l’area
del triangolo iniziale, mentre il segmento CA’ la aumenta. Quindi l’incremento
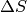 ottenuto grazie a
ottenuto grazie a 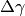 è la differenza fra le aree
è la differenza fra le aree
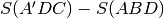 . Per calcolare l’area S(A’DC) la approssimiamo a quella del triangolo A’AC che a sua volta è approssimabile al settore circolare di centro C e
arco
. Per calcolare l’area S(A’DC) la approssimiamo a quella del triangolo A’AC che a sua volta è approssimabile al settore circolare di centro C e
arco 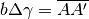 .
In conclusione
.
In conclusione 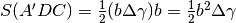 . Fissiamo E , proiezione di A su A’B .
Avremo
. Fissiamo E , proiezione di A su A’B .
Avremo 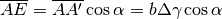 .
Approssimiamo anche il triangolo ABD al triangolo ABE e questo ,a sua volta, al
settore circolare di arco AE e angolo
.
Approssimiamo anche il triangolo ABD al triangolo ABE e questo ,a sua volta, al
settore circolare di arco AE e angolo 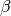 . Quindi
. Quindi 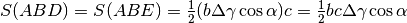 .
La differenza (approssimata) delle due aree risulta
.
La differenza (approssimata) delle due aree risulta 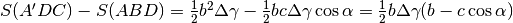 . L’espressione tra parentesi equivale a
. L’espressione tra parentesi equivale a 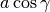 ,
quindi, alla fine abbiamo
,
quindi, alla fine abbiamo 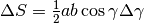 , che è la stessa espressione utilizzata per risolvere il problema.
, che è la stessa espressione utilizzata per risolvere il problema.
Come si vede, l’uso delle derivate ci risparmia un percorso deduttivo tutt’altro che immediato.
Problema 3: La bolla¶
Una bolla di sapone del raggio di 8.5 cm pesa 0.24 grammi. Quale è il suo spessore?
Si immagina che la densità dell’acqua saponata sia di 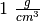 e quindi
la bolla ha volume di
e quindi
la bolla ha volume di 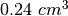 . Il volume è un sottile guscio sferico, di
raggio interno pari a r e spessore
. Il volume è un sottile guscio sferico, di
raggio interno pari a r e spessore 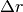 molto piccolo rispetto a r.
Possiamo pensare di descrivere il volume del guscio come la differenza fra due sfere concentriche:
molto piccolo rispetto a r.
Possiamo pensare di descrivere il volume del guscio come la differenza fra due sfere concentriche: 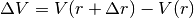 , con
, con 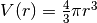 . Applicando la formula esatta della differenza, abbiamo:
. Applicando la formula esatta della differenza, abbiamo: 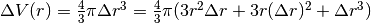 cioé
un’equazione di terzo grado in
cioé
un’equazione di terzo grado in 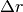 , complicata da risolvere.
, complicata da risolvere.
Invece la formula approssimata ci dà:
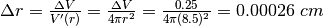 .
.
Note
La formula risolutiva approssimata è sempre un’equazione di primo grado in 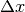 .
.
Problema 4: Il numero di Eulero¶
Il numero di Eulero 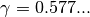 viene utilizzato nel calcolo
viene utilizzato nel calcolo 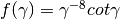 . Qual’è il minimo numero di decimali da utilizzare
in
. Qual’è il minimo numero di decimali da utilizzare
in 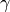 per avere un errore massimo di 0.001?
per avere un errore massimo di 0.001?
La funzione 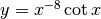 ha per derivata
ha per derivata 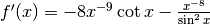 . Se
. Se 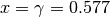 e
e 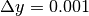 , calcolando
, calcolando
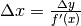 si ottiene
si ottiene 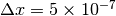 ,
un numero con 7 cifre decimali. Quindi la risposta è 7 cifre decimali.
,
un numero con 7 cifre decimali. Quindi la risposta è 7 cifre decimali.
Verifichiamo. Con 15 cifre decimali, il numero 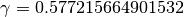 ,
quindi con 7 decimali è
,
quindi con 7 decimali è 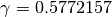 . Provando a calcolare
. Provando a calcolare
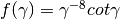 con i valori
con i valori 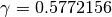 e
e
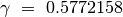 , cioé aumentando e poi diminuendo di uno l’ultima
cifra decimale, si ottengono
, cioé aumentando e poi diminuendo di uno l’ultima
cifra decimale, si ottengono 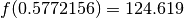 e
e 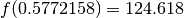 ,
che sono risultati uguali a meno di 0.001. Se riproviamo fermandoci a 6 cifre
decimali e calcolando la funzione con la sesta cifra decimale variata di un’unità,
stavolta i risultati differiscono di più di un millesimo.
,
che sono risultati uguali a meno di 0.001. Se riproviamo fermandoci a 6 cifre
decimali e calcolando la funzione con la sesta cifra decimale variata di un’unità,
stavolta i risultati differiscono di più di un millesimo.
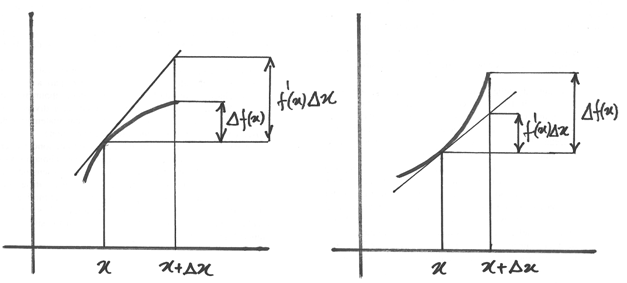
La contrazione dell’errore¶
Quale ragionamento guida la soluzione del problema 4? Se usiamo una funzione con
un numero approssimato 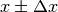 avremo un risultato anch’esso
approssimato
avremo un risultato anch’esso
approssimato 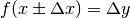 . Se
. Se 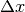 è piccolo
possiamo usare la formula approssimata
è piccolo
possiamo usare la formula approssimata 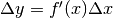 , che equivale
ad approssimare il grafico della funzione nel punto di ascissa x con la tangente.
La derivata avrà segno positivo o negativo a seconda che gli incrementi siano di
segno concorde o discorde. Ma se consideriamo solo i valori assoluti degli incrementi,
allora avremo
, che equivale
ad approssimare il grafico della funzione nel punto di ascissa x con la tangente.
La derivata avrà segno positivo o negativo a seconda che gli incrementi siano di
segno concorde o discorde. Ma se consideriamo solo i valori assoluti degli incrementi,
allora avremo 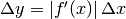 .
. 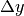 può essere pensato come incremento oppure come approssimazione (errore assoluto)
del valore della funzione, e analogamente
può essere pensato come incremento oppure come approssimazione (errore assoluto)
del valore della funzione, e analogamente 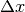 .
.
- Se la derivata vale 1 (in valore assoluto),
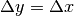 , l’errore sulla variabile è uguale all’errore sulla funzione.
, l’errore sulla variabile è uguale all’errore sulla funzione. - Se
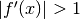 , allora la funzione dilata l’errore.
, allora la funzione dilata l’errore. - Se infine
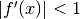 , significa che la funzione “reagisce”
all’incremento
, significa che la funzione “reagisce”
all’incremento 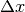 con un incremento minore: la funzione contrae
l’errore.
con un incremento minore: la funzione contrae
l’errore.
Il metodo delle contrazioni per approssimare la soluzione delle equazioni si basa su questo principio.
Riassunto¶
- Se
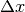 è piccolo si può approssimare la formula
è piccolo si può approssimare la formula 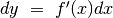 con la formula
con la formula 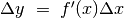 . L’approssimazione è utile,
a volte indispensabile, nei problemi in cui si chiede di ricavare l’incremento
. L’approssimazione è utile,
a volte indispensabile, nei problemi in cui si chiede di ricavare l’incremento
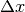 che provoca un dato incremento
che provoca un dato incremento 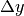 .
. - L’equazione risolutiva approssimata
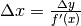 è di primo grado ed è di facile soluzione. Al contrario, non sempre è facile
o possibile dedurre la formula risolutiva dall’equazione esatta
è di primo grado ed è di facile soluzione. Al contrario, non sempre è facile
o possibile dedurre la formula risolutiva dall’equazione esatta
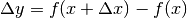 .
. - In alcuni problemi, per i quali entrambe le formule sono utilizzabili, si confronta la soluzione esatta con quella approssimata e si può verificare come la soluzione approssimata sia ampiamente sufficiente.
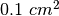 ?
?