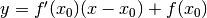La tangente¶
In questo capitolo impariamo a calcolare e utilizzare l’equazione della retta tangente e poi prendiamo confidenza con la funzione derivata, valutando per via grafica la tangente a varie curve.
Ricerca della retta tangente¶
Dato che la derivata, se esiste, fornisce la pendenza della retta tangente al grafico di f(x),
sarà facile scrivere l’equazione della retta tangente in  a una curva f(x).
L’equazione di una retta per il punto
a una curva f(x).
L’equazione di una retta per il punto 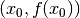 è
è 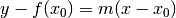 .
Il coefficiente angolare m è dato dalla derivata calcolata nel punto, quindi la tangente è:
.
Il coefficiente angolare m è dato dalla derivata calcolata nel punto, quindi la tangente è:
Esercizi svolti¶
1. Trova il punto della parabola 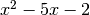 in cui la tangente è parallela
alla retta
in cui la tangente è parallela
alla retta 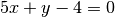
Abbiamo il risultato della derivata nel punto cercato: è -5, il coefficiente angolare della retta parallela alla tangente. Calcoliamo quindi l’espressione della derivata e cerchiamo il punto in cui essa vale -5.
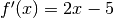 . Perché la derivata valga -5 deve essere x=0 . In questo punto la funzione vale -2, quindi il punto cercato è (0,-2).
. Perché la derivata valga -5 deve essere x=0 . In questo punto la funzione vale -2, quindi il punto cercato è (0,-2).
2. Data la funzione 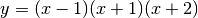 , trova la tangente e la normale al
suo grafico nei punti di intersezione con l’asse delle ascisse.
, trova la tangente e la normale al
suo grafico nei punti di intersezione con l’asse delle ascisse.
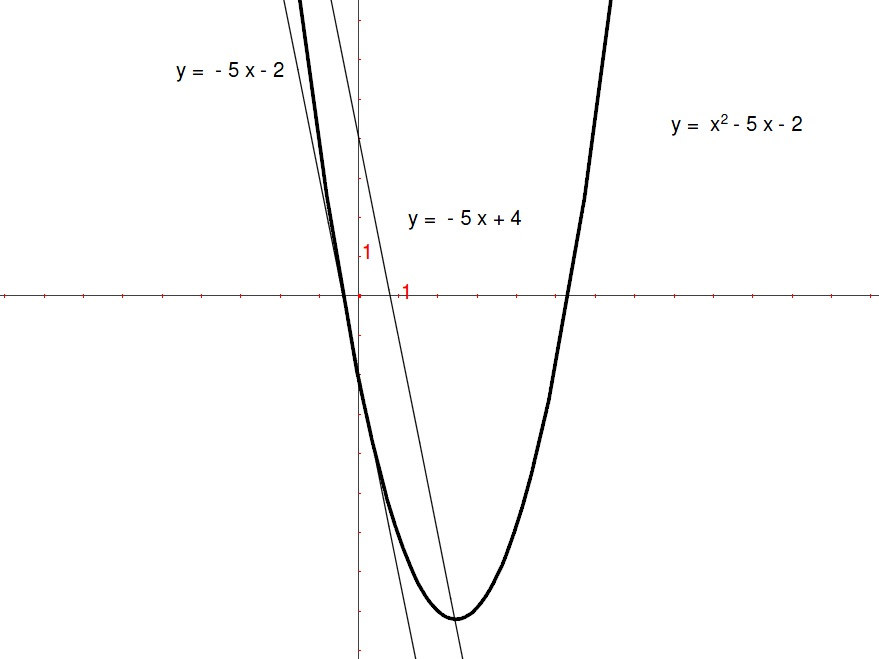
La funzione si azzera per x=1 , x=-1 , x=-2 . Occorre calcolare la derivata in questi punti e poi esprimere per ogni punto l’equazione della retta tangente e quella della retta normale, che avrà il coefficiente angolare antireciproco. Per il calcolo della derivata, ci sono tre vie. Si potrebbe prima esprimere il polinomio, svolgendo il prodotto, e poi derivare. Oppure si moltiplicano i due primi binomi, poi si segue la regola del prodotto:
.
Il terzo modo è descritto nel prossimo paragrafo.
Il calcolo della derivata, dopo semplici passaggi algebrici, ci dà: 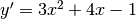 . Nel primo punto (-2,0) avremo:
. Nel primo punto (-2,0) avremo:
- per la tangente
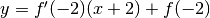
- per la normale:
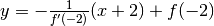 .
.
Dato che 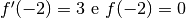 ne risulta:
ne risulta: 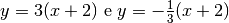 per la tangente e per la normale. Per gli altri punti lo svolgimento è lo stesso.
per la tangente e per la normale. Per gli altri punti lo svolgimento è lo stesso.
3. Dimostra che i segmenti tangenti all’iperbole equilatera 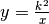 ,
compresi fra gli assi coordinati, hanno per punto medio il punto di tangenza.
,
compresi fra gli assi coordinati, hanno per punto medio il punto di tangenza.
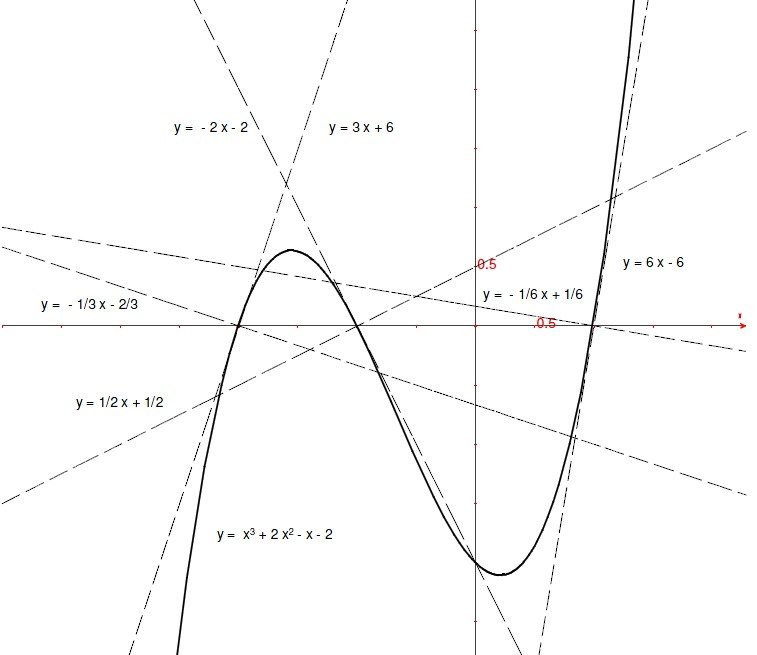
Calcoliamo la derivata e poi scriviamo l’eq.della tangente per un generico punto dell’iperbole 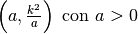 (limitiamoci al primo quadrante).
(limitiamoci al primo quadrante).
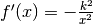 e per la tangente in a
e per la tangente in a 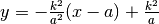 .
.
Le intersezioni della tangente con gli assi sono in 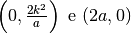 .
Allora il punto medio è
.
Allora il punto medio è 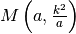 , che è proprio il punto di tangenza.
, che è proprio il punto di tangenza.
Derivare un prodotto di più funzioni¶
La terza possibilità è imparare a derivare le funzioni che contengono più prodotti. Nel caso di tre funzioni: 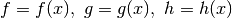
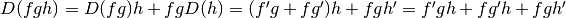 .
.
È una regola che si estende a più prodotti: si scrive una somma in cui
compaiono tanti prodotti delle funzioni quante sono le funzioni e all’interno
di ogni prodotto si deriva una funzione diversa.
Così per esempio 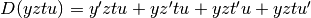 dove per brevità
intendiamo che y, z, t, u siano tutte funzioni di
dove per brevità
intendiamo che y, z, t, u siano tutte funzioni di 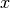 .
.
Come varia la tangente¶
Immaginiamo di calcolare la derivata relativa a punti diversi del grafico di una funzione: otterremo diversi valori che graficamente rappresentano le diverse inclinazioni della retta tangente alla curva. Se visualizziamo una dopo l’altra queste tangenti, avremo l’impressione di “costeggiare” la curva che rappresenta la funzione. Nei nostri esempi la pendenza è una funzione continua, legata all’andamento della primitiva: si può quindi mettere in grafico sia la funzione data, la primitiva, sia la funzione derivata.
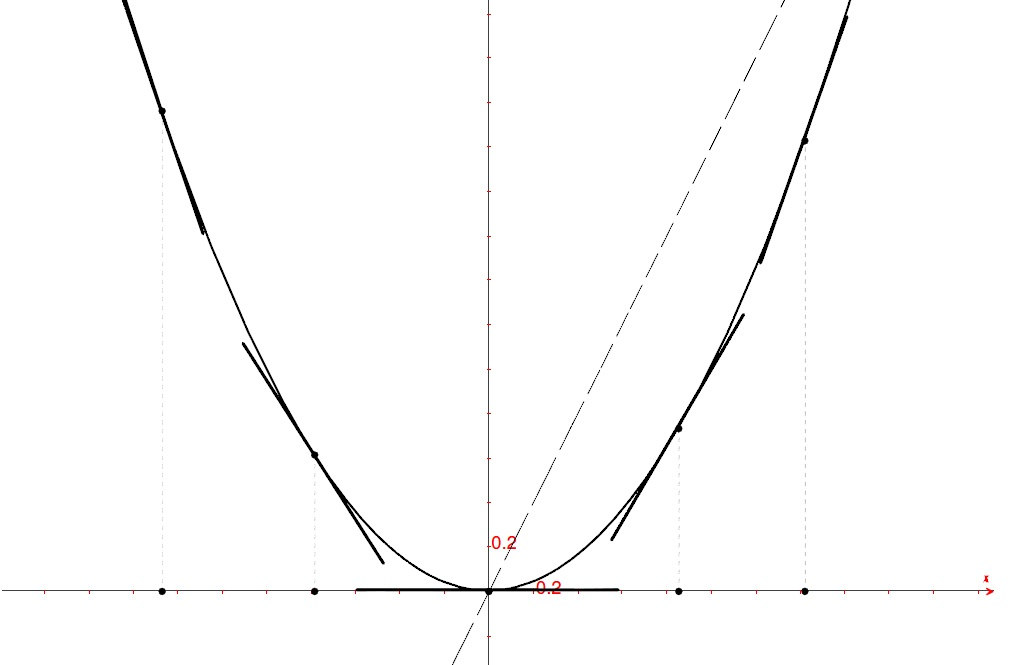
Tangenti ad una parabola¶
La parabola 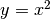 ha per derivata
ha per derivata 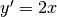 , che è quindi una retta. I punti di questa retta rappresentano le diverse inclinazioni delle tangenti alla parabola, che al crescere di x diventano sempre meno decrescenti, raggiungono la direzione orizzontale in corrispondenza del vertice della parabola, poi aumentano sempre più la propria inclinazione, proporzionalmente a x.
, che è quindi una retta. I punti di questa retta rappresentano le diverse inclinazioni delle tangenti alla parabola, che al crescere di x diventano sempre meno decrescenti, raggiungono la direzione orizzontale in corrispondenza del vertice della parabola, poi aumentano sempre più la propria inclinazione, proporzionalmente a x.
La funzione derivata cresce quindi costantemente secondo una retta che passa per l’origine, crescendo da valori negativi a valori positivi man mano che la parabola attenua la sua decrescita, per poi risalire.
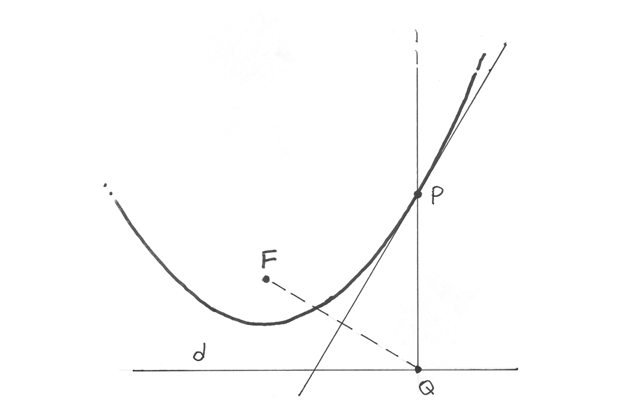
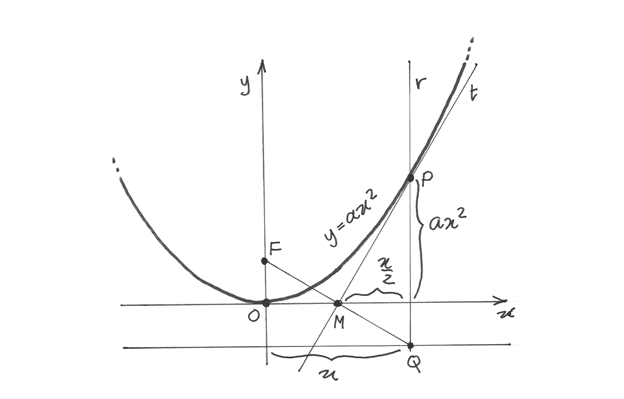
Il fatto che sia proprio una retta a descrivere la variabilità della tangente si spiega anche con la costruzione geometrica del grafico della parabola, i cui punti P si trovano all’intersezione
fra due rette: la retta r , perpendicolare in Q alla direttrice e l’asse t del segmento che unisce
Q al fuoco F. In questo modo t è la tangente alla parabola e il suo coefficiente angolare è
dato da 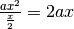 , ( x è l’ascissa di Q e per ragioni di
simmetria
, ( x è l’ascissa di Q e per ragioni di
simmetria 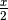 è l’intersezione di t con l’asse orizzontale).
è l’intersezione di t con l’asse orizzontale).
2ax è proprio la derivata della funzione parabola e per semplificare nel nostro esempio abbiamo preso a=1
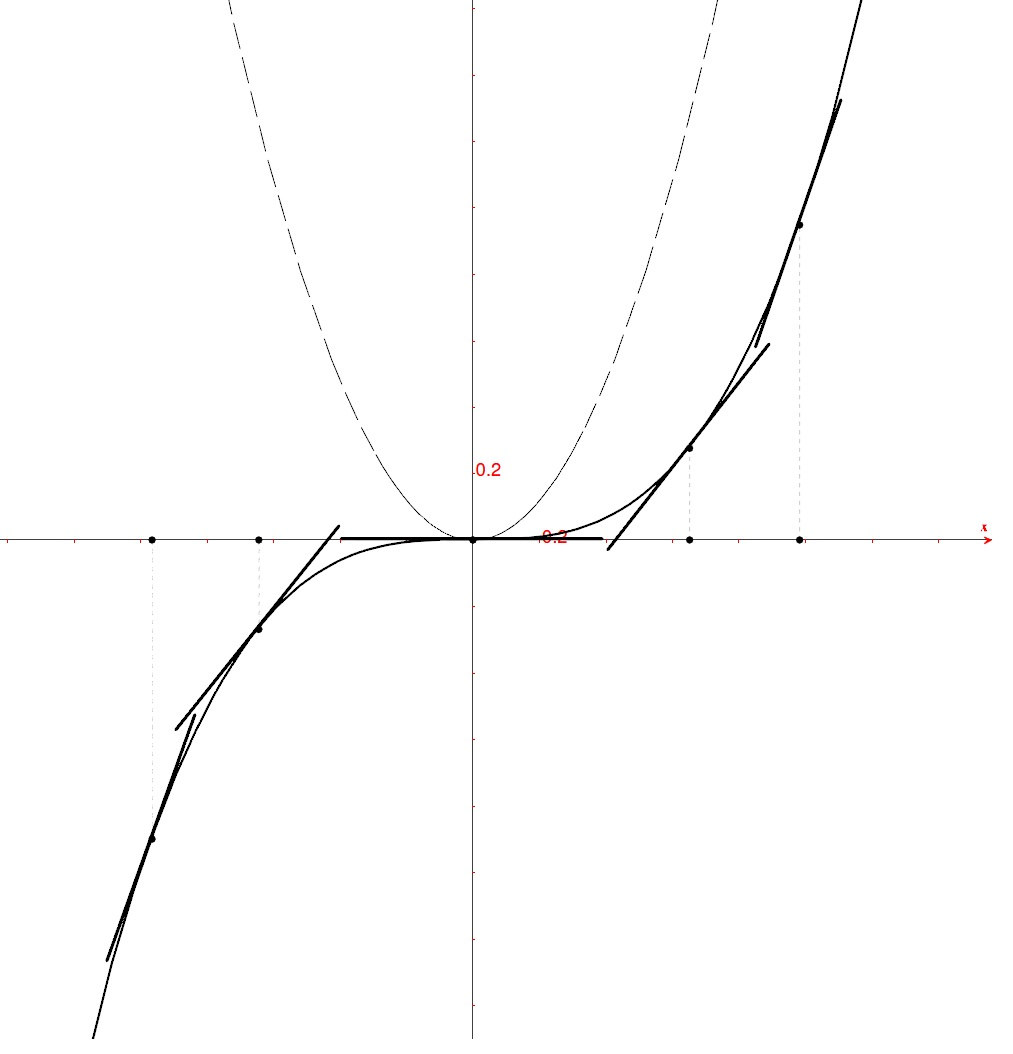
Tangenti ad una cubica¶
La funzione associa ad ogni numero x il suo cubo. La funzione è crescente, quindi, procedendo
da sinistra verso destra, i valori della funzione sono sempre meno negativi e i rapporti differenziali sono positivi. Per es. prendiamo per semplicità il rapporto incrementale relativamente a x=-3 :
si ha 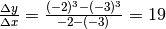 . E’ facile
verificare che questi rapporti, pur mantenendosi sempre positivi, diminuiscono e
tendono ad azzerarsi nei pressi dell’origine, per poi tornare a crescere.
. E’ facile
verificare che questi rapporti, pur mantenendosi sempre positivi, diminuiscono e
tendono ad azzerarsi nei pressi dell’origine, per poi tornare a crescere.
Di conseguenza le tangenti saranno sempre inclinate positivamente, con tendenza a
diventare orizzontali vicino all’origine. Perciò il grafico della derivata
non potrà essere una retta, come nel caso precedente.
Dato un punto generico della cubica 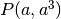 , l’equazione della tangente
per P sarà
, l’equazione della tangente
per P sarà 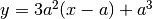 . Il grafico della derivata è una parabola
concava verso l’alto.
. Il grafico della derivata è una parabola
concava verso l’alto.
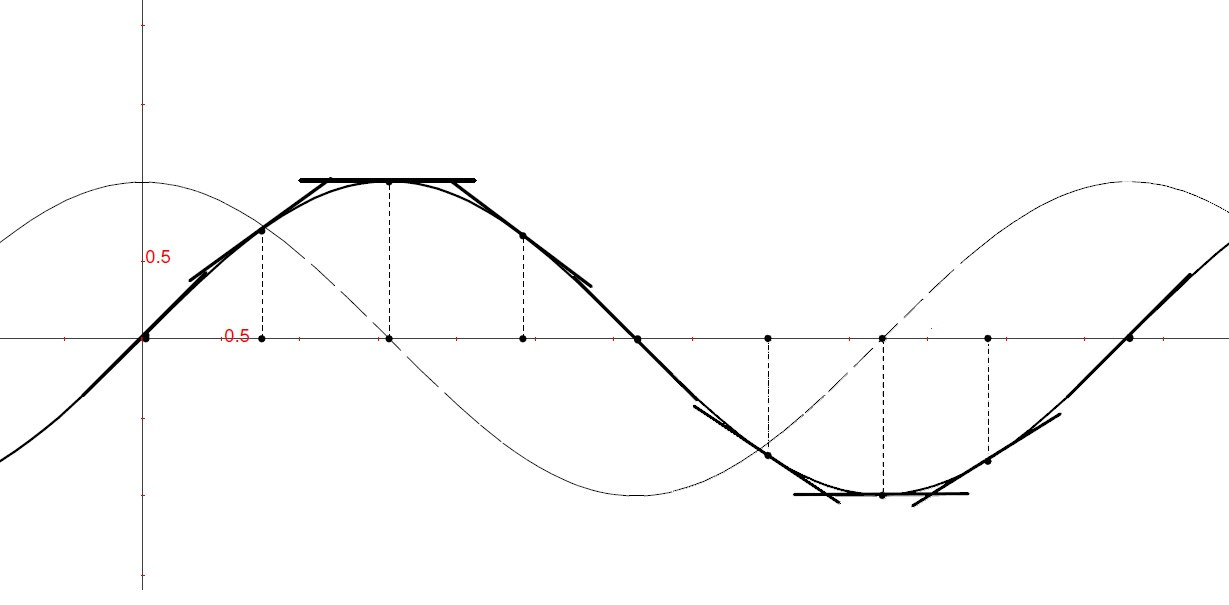
Tangenti alla funzione seno¶
Questa volta abbiamo una funzione oscillante, cioé crescente per alcuni valori, decrescente per altri, che quindi varia fra massimi e minimi successivi.
Le tangenti, di conseguenza saranno inclinate positivamente, poi sempre meno, poi diverranno orizzontali, poi inclinate negativamente, torneranno quindi di nuovo orizzontali e poi crescenti. Poi tutto ricomincerà da capo, nello stesso modo. Anche la funzione derivata è quindi una funzione periodica, legata strettamente al seno. Noi non siamo ancora in grado di esprimere questa derivata, quindi ne facciamo solo una descrizione qualitativa.
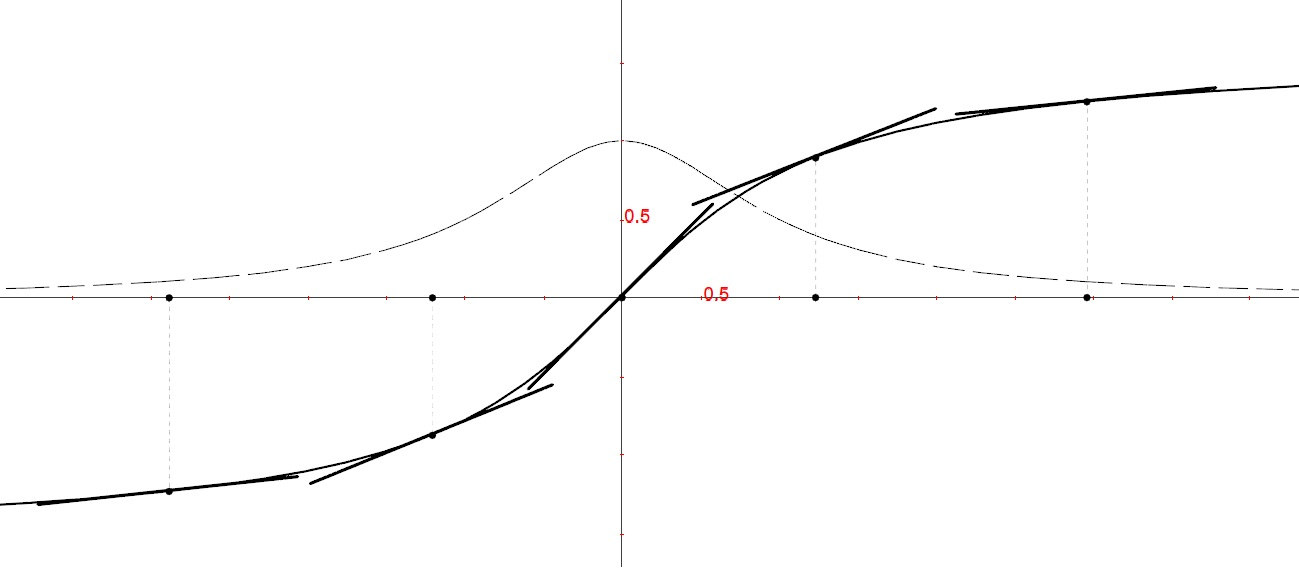
Tangenti alla funzione arcotangente¶
Le tangenti a questa funzione sono tutte rette crescenti (hanno pendenza positiva). La loro pendenza però cresce solo fino a 1, per poi calare gradualmente e diventare 0 all’infinito. Anche questa derivata sarà calcolata più avanti.
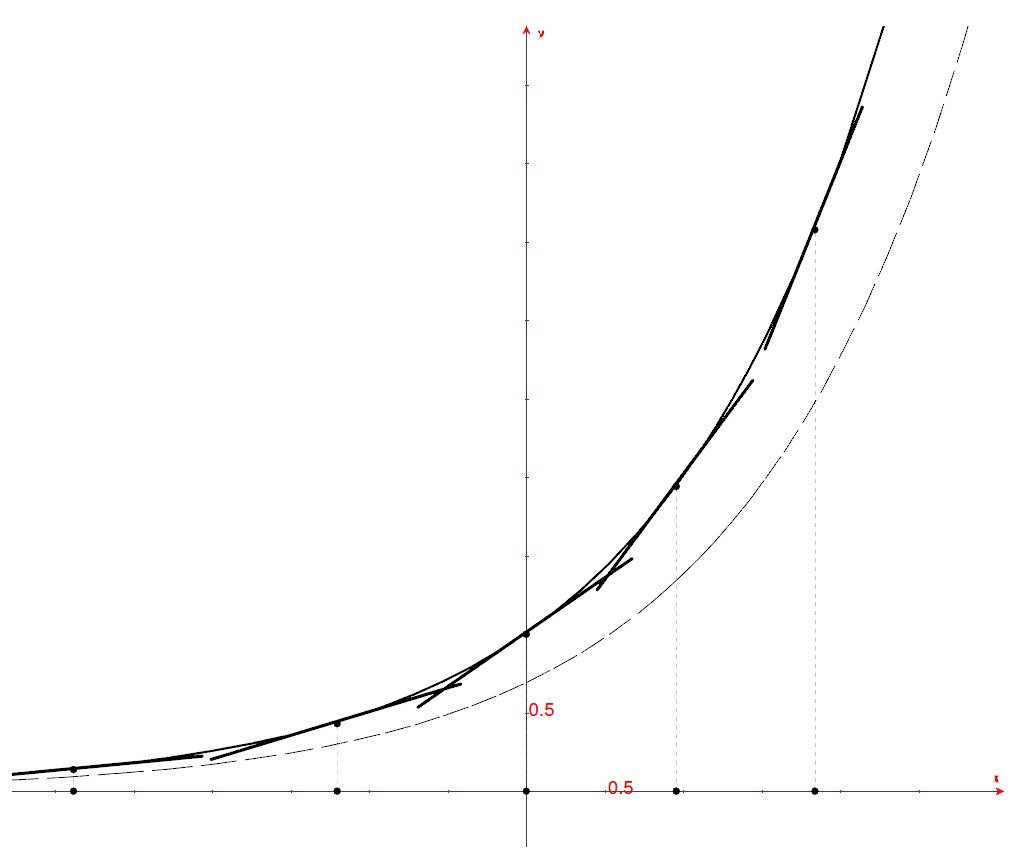
Tangenti ad una funzione esponenziale¶
Le tangenti a questo grafico hanno pendenza sempre più crescente, così come sempre più crescente è la funzione 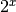 .
.
Quindi il grafico della funzione derivata in un certo senso accompagna il grafico della funzione esponenziale e sembra anch’esso esponenziale, seppur leggermente diverso. Sembrerebbe quindi abbastanza facile risalire dal grafico della primitiva al grafico della derivata e anche il viceversa.
Riassunto¶
- Non è difficile, conoscendo la derivata in un punto, ricavare l’equazione della sua tangente per quel punto e tracciarla.
- L’insieme delle tangenti segue la curva della funzione, accompagnandola e mettendo in evidenza il suo andamento crescente o decrescente.
- Dall’analisi del grafico della derivata si possono quindi trarre utili informazioni sull’andamento della primitiva.
Esercizi¶
- Completa l’es. svolto 2 sul prodotto di più funzioni.
- Ripeti l’es. 3 sulle tangenti all’iperbole nel caso di un altro ramo di iperbole.
- Con l’aiuto di un software come Geogebra, disegna il grafico di
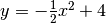 , osserva le tangenti al grafico e l’andamento della
funzione tangente. Sulla stessa pagina traccia il grafico della funzione derivata.
, osserva le tangenti al grafico e l’andamento della
funzione tangente. Sulla stessa pagina traccia il grafico della funzione derivata. - Ripeti l’es.precedente per la parabola:
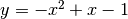 .
. - La retta
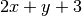 potrebbe rappresentare la derivata di quale parabola?
potrebbe rappresentare la derivata di quale parabola? - Ripeti l’es.3 relativamente alle cubiche
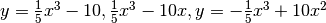 scrivendo le tue osservazioni.
scrivendo le tue osservazioni. - Quale funzione richiama il grafico della derivata della funzione
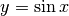 ?
? - Traccia il grafico della funzione
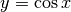 e descrivi l’andamento delle tangenti.
e descrivi l’andamento delle tangenti.