La derivata: definizione e prime regole di derivazione¶
Introduzione¶
Consideriamo l’informazione che otteniamo da un valore di velocità media fra due istanti di tempo: si tratta di un’informazione sulla media, cioé senza dettagli sulle variazioni di velocità che possono essere avvenute durante quel periodo di tempo. Per queste informazioni più puntuali dovremmo poter suddividere l’intervallo di tempo in periodi molto piccoli, in frazioni di secondo sempre minori. La velocità media relativa al periodo fra due istanti di tempo così vicini da quasi coincidere viene detta velocità istantanea, ed è quella indicata da un tachimetro.
Abbiamo già considerato, nel capitolo precedente, che il tasso medio di variazione di una funzione, relativamente a un intervallo del suo dominio, non dà informazioni sulle variazioni puntuali della funzione nell’intervallo considerato.
Questo capitolo si concentra sul modo migliore che consente di arrivare al tasso di variazione di una funzione continua, analogo alla ricerca di calcolare una velocità istantanea. Terremo conto di quanto visto nel cap.6 per l’uso delle differenze infinitesime e arriveremo a definire qualcosa di analogo alla velocità istantanea. Nel moto vario essa è una funzione che fornisce un valore finito, ad un certo istante. Nell’analisi non standard il risultato analogo, il tasso di variazione, si otterrà operando sugli iperreali.
Derivata¶
Esauriti i discorsi di base sulle differenze, torniamo ora al punto principale: definire il tasso di variazione relativo ad una funzione a
dominio continuo. Come abbiamo visto a proposito delle funzioni a dominio discreto, si tratterà
di definire il rapporto delle differenze, cioé nel nostro caso dei differenziali.
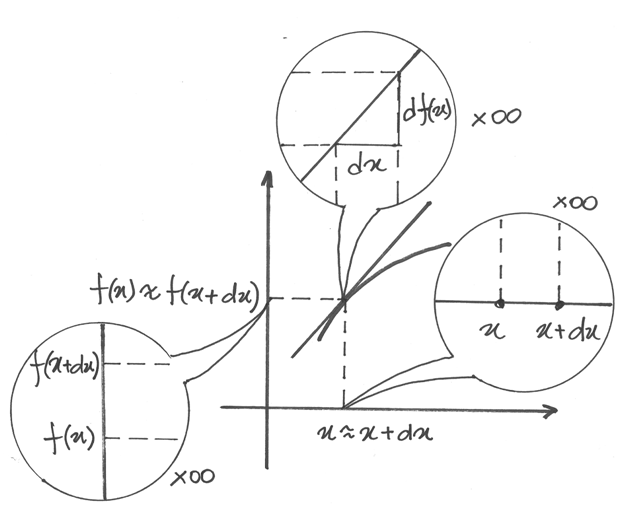
Il rapporto incrementale, relativo ad un incremento infinitesimo non nullo dx, è detto rapporto
differenziale, ed è un numero iperreale dato da 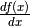 .
.
Il tasso di variazione si otterrà dalla parte standard di questo rapporto, a due condizioni:
- che il rapporto abbia un valore finito
- che la parte standard non cambi al cambiare di dx.
Il concetto è così importante che ha un nome particolare:
Si dice derivata di una funzione 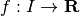 in un suo punto
di continuità x di I, la parte standard del rapporto differenziale
in un suo punto
di continuità x di I, la parte standard del rapporto differenziale
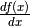 , purché esista con valore finito e sia indipendente
dalla scelta del particolare dx usato.
, purché esista con valore finito e sia indipendente
dalla scelta del particolare dx usato.
Il simbolo che si usa per questo nuovo calcolo è f’(x), oppure Df(x),
con il significato già detto: 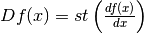 .
Il nome derivata ha ragioni storiche: si tratta di una nuova funzione che
appunto deriva da un’altra data, esprimendo punto per punto il tasso di
variazione di questa, che viene detta funzione primitiva.
.
Il nome derivata ha ragioni storiche: si tratta di una nuova funzione che
appunto deriva da un’altra data, esprimendo punto per punto il tasso di
variazione di questa, che viene detta funzione primitiva.
Significato geometrico¶
Il rapporto differenziale 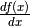 esprime geometricamente la
pendenza della retta secante alla curva per i punti
esprime geometricamente la
pendenza della retta secante alla curva per i punti 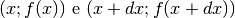 , che sono fra loro infinitamente vicini. Quindi la derivata, essendo la
parte standard del rapporto differenziale, sarà
la pendenza della tangente al grafico della funzione, nel punto di ascissa x.
, che sono fra loro infinitamente vicini. Quindi la derivata, essendo la
parte standard del rapporto differenziale, sarà
la pendenza della tangente al grafico della funzione, nel punto di ascissa x.
Quando la derivata non esiste¶
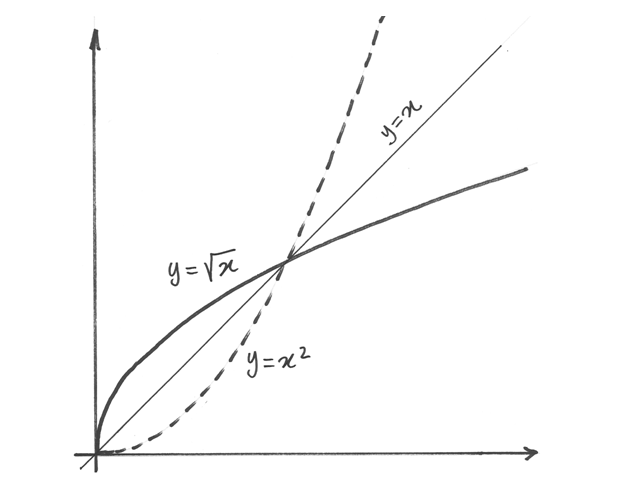
Prendiamo il caso di 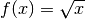 . Il suo grafico ha tangente verticale
in x =0.
Infatti si tratta della funzione inversa rispetto a
. Il suo grafico ha tangente verticale
in x =0.
Infatti si tratta della funzione inversa rispetto a 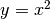 , che nello
stesso punto ha tangente orizzontale.
, che nello
stesso punto ha tangente orizzontale.
Calcoliamo il rapporto differenziale in x =0:
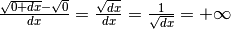 .
La parte standard del rapporto differenziale non è quindi calcolabile. Per inciso,
l’infinito è positivo perché la funzione è definita solo per numeri positivi.
Se un numero qualsiasi z è un infinito negativo, scriveremo
.
La parte standard del rapporto differenziale non è quindi calcolabile. Per inciso,
l’infinito è positivo perché la funzione è definita solo per numeri positivi.
Se un numero qualsiasi z è un infinito negativo, scriveremo 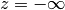 .
Nel caso di un infinito generico:
.
Nel caso di un infinito generico: 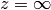
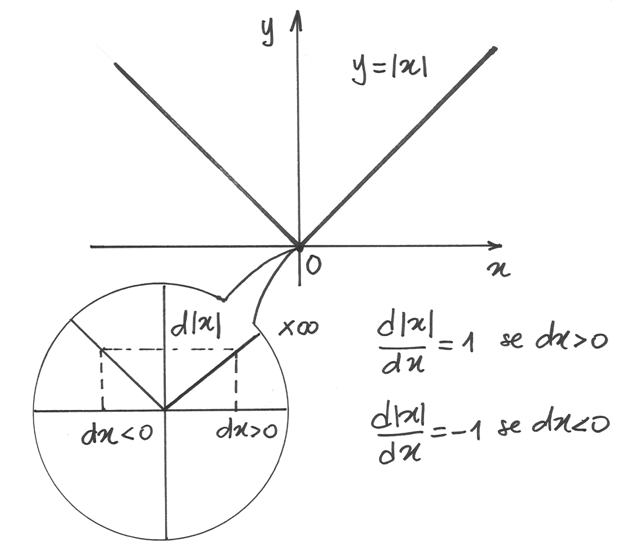
La derivata può non esistere anche se la tangente non è verticale. E’ il caso di un punto angoloso, cioé un punto, visto al microscopio non standard, per il quale il rapporto differenziale cambia a seconda dell’infinitesimo scelto come incremento.
Nell’esempio del disegno questo fatto è visibile anche al microscopio standard.
La funzione è 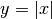 e in x =0 il rapporto differenziale vale +1 se dx
è positivo, -1 se dx è negativo.
e in x =0 il rapporto differenziale vale +1 se dx
è positivo, -1 se dx è negativo.
In conclusione, l’esistenza della derivata si traduce nel fatto che il grafico, osservato al microscopio non standard nel punto considerato, è indistinguibile da un segmento orizzontale o obliquo (non verticale).
Primi calcoli¶
Per il primo esempio di calcolo, seguiamo la definizione. Data la funzione, occorrerà
- esprimere il differenziale df(x)
- scrivere il rapporto differenziale
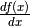
- calcolare la parte standard
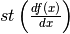
Calcolo di Df(x), con 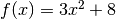 . La sequenza è:
. La sequenza è:
Quindi 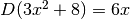 .
.
Un secondo modo è più diretto. Si calcola dapprima il differenziale e poi si utilizza solo la sua parte principale, che è indistinguibile. Al termine si scrive il rapporto differenziale e si calcola la sua parte standard. Quindi, data la stessa funzione:
Il segno di indistinguibilità viene usato per esattezza, perché due espressioni indistinguibili non sono (in genere) esattamente uguali. Tuttavia per praticità
è accettabile usare il segno di uguale, anche quando l’uguaglianza si riferisce alla sola parte standard.
Così d’ora in avanti intenderemo che 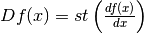 equivalga a
equivalga a
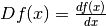 , anche se la prima uguaglianza è esatta mentre
la seconda è approssimata.
, anche se la prima uguaglianza è esatta mentre
la seconda è approssimata.
Regole generali¶
Dalle regole per il calcolo del differenziale delle funzioni deduciamo facilmente le regole per il calcolo della derivata. Basta usare la definizione di rapporto differenziale.
Note
La regola del prodotto, estesa a più funzioni, viene illustrata all’inizio del prossimo capitolo.
Derivare funzioni potenza¶
Ricaveremo la regola generale per gradi. Calcoliamo dapprima i differenziali,
ricordando il Par.6.5.
Iniziamo da 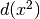 , pensando
, pensando 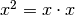 e applicando la regola del prodotto, poi ricominciamo con esponenti via via maggiori.
e applicando la regola del prodotto, poi ricominciamo con esponenti via via maggiori.
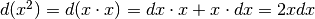
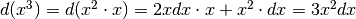
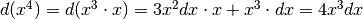
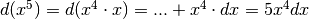
- ...
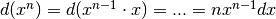
La riga finale, che è intuibile, può essere rigorosamente dimostrata per induzione, seguendo la stessa tecnica. Siamo ora in grado di esprimere la nuova regola:
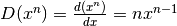 .
.
Cosa succede con esponenti negativi?
La dimostrazione più breve si ottiene sostituendo l’esponente:
infatti, ponendo 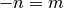 possiamo calcolare la derivata con la regola
nota:
possiamo calcolare la derivata con la regola
nota: 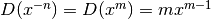 e sostituendo
e sostituendo 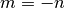 otteniamo la formula cercata
otteniamo la formula cercata 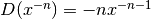 .
.
Note
La regola sulla derivata di una potenza ricorda molto da vicino la regola delle differenze dei fattoriali decrescenti.
Potenze a esponente razionale¶
La regola non cambia se la potenza ha un esponente razionale. Se segui
la regola ti sarà facile concludere, per esempio, che
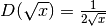 . Si tratta di una regola di validità generale, cioé è
applicabile per le potenze a esponente reale qualsiasi, ma per il momento
non siamo in grado di dimostrarlo. Ci accontentiamo per ora di dimostrare
la validità della regola nel caso delle radici quadrate e cubiche.
. Si tratta di una regola di validità generale, cioé è
applicabile per le potenze a esponente reale qualsiasi, ma per il momento
non siamo in grado di dimostrarlo. Ci accontentiamo per ora di dimostrare
la validità della regola nel caso delle radici quadrate e cubiche.
Derivare le radici¶
Vediamo perché 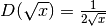 . Dall’espressione
della differenza
. Dall’espressione
della differenza 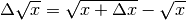 , ricaviamo come differenziale:
, ricaviamo come differenziale: 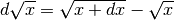 . Si tratta di
un’espressione indistinguibile da zero. Zero è l’unico numero da evitare nelle
questioni di indistinguibilità, per questo riscriviamo il differenziale come se
dovesse essere razionalizzato e cerchiamo l’espressione indistinguibile:
. Si tratta di
un’espressione indistinguibile da zero. Zero è l’unico numero da evitare nelle
questioni di indistinguibilità, per questo riscriviamo il differenziale come se
dovesse essere razionalizzato e cerchiamo l’espressione indistinguibile:
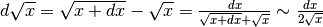 .
Ricordando la convenzione di utilizzare comunque il segno di uguaglianza,
allora la derivata risulta:
.
Ricordando la convenzione di utilizzare comunque il segno di uguaglianza,
allora la derivata risulta:
Questa derivata non è definita per x=0 e infatti abbiamo già verificato che il
grafico della funzione 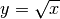 ha tangente verticale nell’origine.
ha tangente verticale nell’origine.
Torniamo ora alla regola della derivata della potenza per individuare una regola conseguente, specifica per le radici. Avremo:
(Tieni presente che l’esponente nella terza espressione 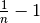 è
un numero negativo). Applichiamo la regola per esempio alla radice cubica:
è
un numero negativo). Applichiamo la regola per esempio alla radice cubica:
![D(\sqrt[3]{x})= D(x^\frac{1}{3})= \frac{x^{\frac{1}{3}-1}}{3}=\frac{x^{-\frac{2}{3}}}{3}=\frac{1}{3x^\frac{2}{3}}=\frac{1}{3\sqrt[3]{x^2}}](../../../_images/math/1c1a5ca38b3b740813179bc79f6192aaf1da0677.png)
Come per la radice quadrata, anche la formula della derivata della radice cubica si può dimostrare a partire dal rapporto differenziale. La razionalizzazione “alla rovescia” in questo caso si esegue ricordando la scomposizione della differenza fra due cubi.
Siamo ora in grado di derivare espressioni di una certa complessità: polinomiali, razionali fratte, irrazionali.
Esercizi svolti¶
I primi esercizi vengono dettagliati minuziosamente. l’obiettivo deve essere acquisire in fretta la pratica che permette di arrivare rapidamente al risultato.
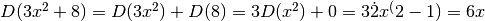 .
.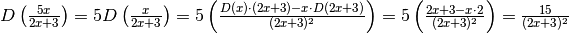
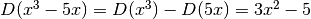
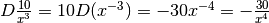
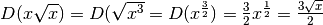 .
.
Quale notazione per la derivata?¶
Usiamo indifferentemente tre notazioni per indicare la stessa cosa: Df(x), 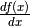 e f’(x). Dato che non facciamo più distinzione fra indistinguibilità e uguaglianza, l’uso di un simbolo o dell’altro risponde solo a un criterio di comodo. Il vantaggio dell’ultimo simbolo sta nell’indicare la
derivata come “funzione derivata” e quindi di poter indicare per esempio f’(2), che
equivale al più laborioso Df(x) per x=2 . Il rapporto differenziale mette in
evidenza la variabile e
per questo è molto usato in fisica e in tecnica. Per esempio
e f’(x). Dato che non facciamo più distinzione fra indistinguibilità e uguaglianza, l’uso di un simbolo o dell’altro risponde solo a un criterio di comodo. Il vantaggio dell’ultimo simbolo sta nell’indicare la
derivata come “funzione derivata” e quindi di poter indicare per esempio f’(2), che
equivale al più laborioso Df(x) per x=2 . Il rapporto differenziale mette in
evidenza la variabile e
per questo è molto usato in fisica e in tecnica. Per esempio 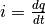 indica che la funzione q varia in dipendenza da t, come avviene per esempio per l’intensità di corrente elettrica.
indica che la funzione q varia in dipendenza da t, come avviene per esempio per l’intensità di corrente elettrica.
Riassunto¶
- La derivata è la parte standard del rapporto differenziale. Per calcolarla, occorre semplicemente scrivere il rapporto differenziale della funzione data e ottenere la sua parte principale.
- La derivata non esiste se il rapporto differenziale è un infinito oppure se dipende da un diverso differenziale dx.
- Le regole di calcolo della derivata di una funzione non elementare si ottengono direttamente da quelle dei differenziali.
- La derivata della funzione potenza segue la regola delle differenze nei fattoriali decrescenti.
- Graficamente, la derivata esprime la pendenza della tangente alla curva per quel punto.
Esercizi¶
- Calcola
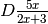 nei due modi descritti nel paragrafo 7.4.
nei due modi descritti nel paragrafo 7.4. - Calcola seguendo le regole generali di calcolo.
- Dimostra la regola della derivata di un prodotto.
- Dimostra la regola della derivata di un quoziente.
- Calcola
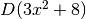 applicando le regole generali del calcolo.
applicando le regole generali del calcolo. - Dimostra che
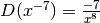 .
. - Seguendo la regola sulla derivata di una potenza, dimostra che
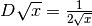 .
. - Dimostra la formula della derivata della radice cubica a partire dal differenziale della funzione.
- Ricalcola l’ultimo esempio, seguendo la regola della derivata di un prodotto.
- Seguendo la regola sulla derivata di una potenza, dimostra che
![D\sqrt[3]{x^5}=\frac{5}{3\sqrt[3]{x^2}}](../../../_images/math/e785fb9b88bdcb6f01aecd5415469a09a986c3d0.png) .
. - Calcola
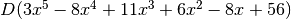
- Calcola
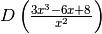
- Calcola
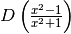
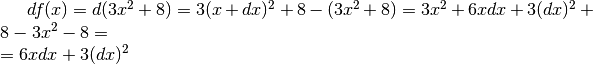
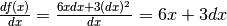
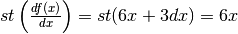
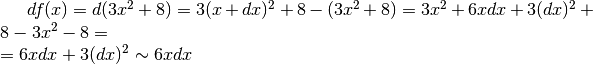
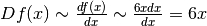
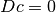
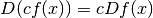
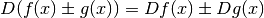
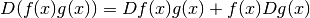

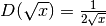
![D(\sqrt[n]{x})=D(x^{\frac{1}{n}})=\frac{1}{n}x^{\frac{1}{n}-1}=\frac{1}{nx^{1-\frac{1}{n}}}=\frac{1}{nx^{\frac{n-1}{n}}}=\frac{1}{n\sqrt[n]{x^{n-1}}}](../../../_images/math/7d65bcdeb71c1092e49b5ef50f1f8f264ebd342c.png)