Il differenziale¶
Introduzione¶
Il tasso medio di variazione di una funzione, relativamente a un intervallo del suo dominio, non dà informazioni sulle variazioni puntuali della funzione nell’intervallo considerato.
Per le funzioni a dominio discreto, che non hanno valori fra due punti distinti successivi, il problema delle informazioni mancanti sulle variazioni all’interno dell’intervallo fra i due punti non si pone. Invece, per le funzioni a dominio continuo il tasso di variazione si può ricercare anche per intervalli molto piccoli del dominio, anche infinitamente piccoli, dato che il dominio è continuo.
Ecco quindi che per avere informazioni sul comportamento puntuale di una funzione a dominio continuo considereremo distanze infinitesime e differenze infinitesime e torneremo ad usare i numeri iperreali.
Funzioni continue¶
Consideriamo l’incremento 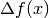 relativo a un incremento infinitesimo
relativo a un incremento infinitesimo 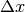 .
In generale, non è detto che anche
.
In generale, non è detto che anche 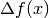 sia infinitesimo.
sia infinitesimo.
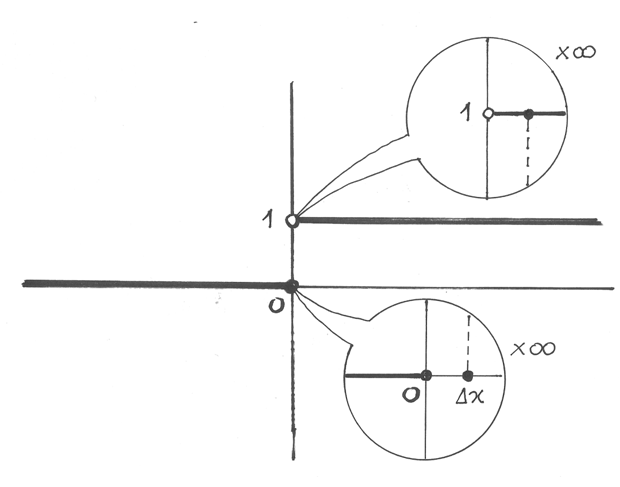
Nel disegno, la funzione ha una discontinuità in x=0 per 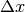 positivo, perché
salta improvvisamente dal valore 0 al valore 1. Eppure si tratta di una funzione a dominio
continuo, cioé definita per ogni valore di x, anche quelli prossimi a 0. La sua espressione analitica è
positivo, perché
salta improvvisamente dal valore 0 al valore 1. Eppure si tratta di una funzione a dominio
continuo, cioé definita per ogni valore di x, anche quelli prossimi a 0. La sua espressione analitica è
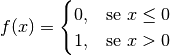
Una funzione di questo tipo si dice discontinua. Al contrario, si dice continua una funzione che ha incrementi infinitesimi dei suoi valori in corrispondenza di incrementi infinitesimi della variabile. Per esprimersi con precisione:
- Una funzione a dominio continuo
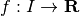 si dice continua nel punto
si dice continua nel punto 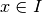 se per ogni infinitesimo
se per ogni infinitesimo 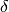 si ha che
si ha che 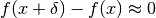 o, in modo equivalente, se per
o, in modo equivalente, se per 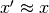 si ha che
si ha che 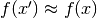 .
.
Diciamo allora che x è un punto di continuità per f. Intendiamo anche che f è continua in un intervallo se tutti i punti dell’intervallo sono di continuità per f.
Differenziale¶
Dunque, per le funzioni continue, a incrementi infinitesimi di x corrispondono incrementi
infinitesimi di f(x).
Per distinguere gli incrementi infinitesimi dagli incrementi standard, useremo
il termine differenziale invece di differenza e useremo la lettera 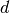 invece della lettera
invece della lettera 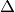 .
.
- Il differenziale della funzione continua f nel punto x, relativo all’incremento infinitesimo
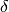 è il numero infinitesimo
è il numero infinitesimo 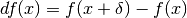 .
.
Nella lettura, df(x) si legge “de effe di x” e la parola differenziale sta per “differenza infinitesimale”. Seguono i primi semplici esempi di calcolo.
Differenziale della funzione identica¶
Il più semplice differenziale è quello della funzione identica 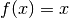 ,
per la quale
,
per la quale 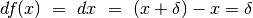 .
Quindi potremo scrivere dx invece di
.
Quindi potremo scrivere dx invece di 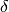 , per indicare l’incremento infinitesimo di x.
Di conseguenza, nell’espressione di un qualsiasi altro differenziale,
al posto di
, per indicare l’incremento infinitesimo di x.
Di conseguenza, nell’espressione di un qualsiasi altro differenziale,
al posto di 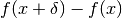 potremo scrivere
potremo scrivere 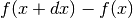 .
.
Differenziale della funzione quadrato¶
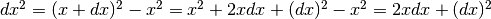 .
.
L’ultimo addendo è un infinitesimo di ordine superiore e si può trascurare. Quindi:
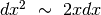 .
.
Si arriva allo stesso risultato in modo più diretto, utilizzando le formule già
viste per le differenze, sostituendo dx al posto di 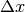 e eliminando gli infinitesimi di ordine superiore. Come negli esempi successivi.
e eliminando gli infinitesimi di ordine superiore. Come negli esempi successivi.
Differenziale della funzione cubo¶
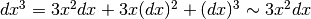 .
.
Differenziale della funzione reciproca¶
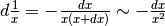 .
.
Parte principale del differenziale¶
Come si vede dai primi esempi, dopo aver sostituito banalmente d al posto
di 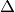 per calcolare il differenziale di una funzione partendo
dall’espressione della sua differenza, si rende più agile il risultato eliminando infinitesimi di ordine superiore. La parte che resta si chiama parte principale.
C’è una regola per scegliere la parte principale di df(x) rispetto a dx?
per calcolare il differenziale di una funzione partendo
dall’espressione della sua differenza, si rende più agile il risultato eliminando infinitesimi di ordine superiore. La parte che resta si chiama parte principale.
C’è una regola per scegliere la parte principale di df(x) rispetto a dx?
In generale, dati due infinitesimi 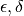 , dire che
, dire che  è dello stesso ordine di
è dello stesso ordine di 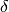 significa che
significa che 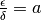 ,
dove a è un finito non infinitesimo. Ne consegue che
,
dove a è un finito non infinitesimo. Ne consegue che 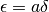 .
Al posto di a potremmo scrivere qualsiasi altro numero indistinguibile da a, senza cambiare significato al confronto. Tutti questi fra loro indistinguibili
hanno la stessa parte standard s, per cui esiste un unico numero standard s tale che
.
Al posto di a potremmo scrivere qualsiasi altro numero indistinguibile da a, senza cambiare significato al confronto. Tutti questi fra loro indistinguibili
hanno la stessa parte standard s, per cui esiste un unico numero standard s tale che
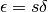 .
. 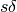 è la parte principale
dell’infinitesimo
è la parte principale
dell’infinitesimo  rispetto all’infinitesimo
rispetto all’infinitesimo 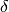 .
La parte principale vale zero nel caso che
.
La parte principale vale zero nel caso che  sia di ordine
superiore rispetto a
sia di ordine
superiore rispetto a 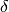 .
.
I tre ultimi esempi di calcolo del differenziale rendono evidente la scelta della parte principale del risultato.
Regole di calcolo¶
Il calcolo del differenziale di una funzione, composta grazie a operazioni fra due funzioni, ha le stesse regole viste per il calcolo delle differenze. Ora però avremo espressioni più semplici, perché alla fine sceglieremo la parte principale del risultato. Queste le prime regole:
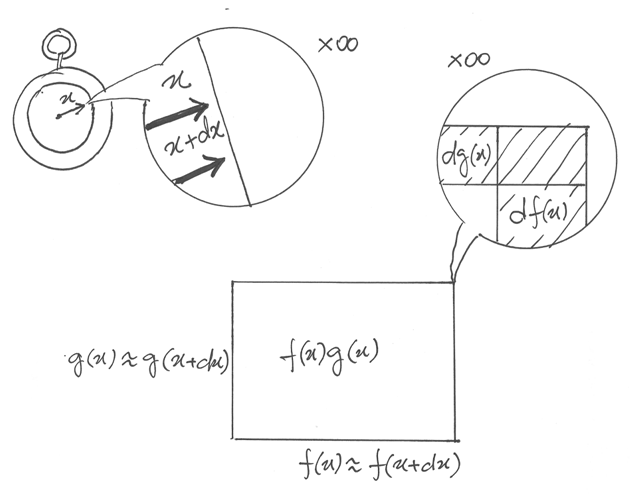
Per chiarire la regola del prodotto, ancora una volta possiamo ricorrere alla geometria.
Rappresentiamo il prodotto fra due funzioni, che nel disegno misurano le dimensioni di un rettangolo. L’incremento differenziale di area avrà ad un vertice un incremento rettangolare trascurabile, perchè infinitesimo di ordine superiore rispetto alle due strisce (superiore e laterale). Quindi nella quarta regola utilizzeremo l’espressione finale, indistinguibile dalla precedente.
L’ultima regola, del rapporto, viene dal fatto che g(x) è una funzione continua e quindi si può utilizzare l’ultima espressione al posto di quella esatta, indistinguibile.
Riassunto¶
- Il fatto che il dominio delle funzioni sia continuo permette di definire l’incremento infinitesimo di x (dx), infinitesimo non nullo.
- Se anche la funzione è continua, allora all’incremento infinitesimo della variabile è associato anche l’incremento infinitesimo della funzione: il suo differenziale df(x).
- Come per le differenze, i differenziali vengono espressi per le funzioni più semplici e si danno le prime regole di calcolo per le operazioni fra funzioni.
- La possibilità di usare quantità infinitesime ci riconduce ai numeri iperreali e si dimostra, attraverso l’uso delle parti principali, che è possibile trascurare gli infinitesimi di ordine superiore, ottenendo così espressioni più semplici rispetto a quelle delle differenze.
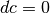
![d[cf(x)]=cdf(x)](../../../_images/math/d02bec3d2f3c19d1c059e0e6d917139812449a91.png)
![d[f(x)\pm g(x)]=df(x) \pm dg(x)](../../../_images/math/337067f91cc4d952b0477aebbd5a5680d961cacf.png)
![d[f(x)g(x)]=df(x)g(x)+f(x)dg(x)+df(x)dg(x)\sim df(x)g(x)+f(x)dg(x)](../../../_images/math/0c91a9845d9d1337dc92ed3315b0957394ae5b2a.png)
![d\left[\frac{f(x)}{g(x)}\right]=\frac{df(x)g(x)-f(x)dg(x)}{g(x)g(x+dx)}\sim\frac{df(x)g(x)-f(x)dg(x)}{g(x)^2}](../../../_images/math/e25d87c19974fd746ce96bf5e7fbc1ddb660a41a.png)