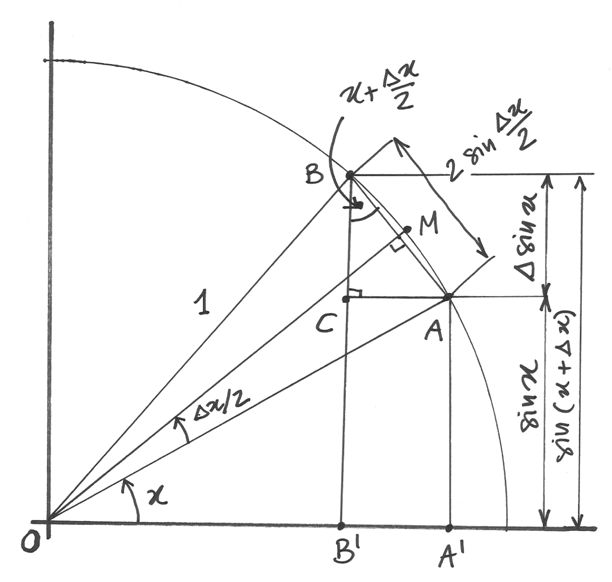
Le funzioni e il rapporto incrementale¶
Rapporto incrementale in funzioni a dominio discreto¶
Una funzione a dominio discreto in generale è diversa da una successione perché il suo dominio è una successione crescente qualsiasi, quindi non è detto che sia esclusivamente la successione degli indici.
L’esempio seguente illustra una funzione a dominio discreto 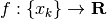 . La scrittura
. La scrittura 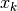 , (anziché k come sarebbe per una successione) ci dice che il dominio è
una successione crescente di interi e la tabella che rappresenta la funzione ha 3 righe:
gli indici, i valori del dominio e i valori del codominio.
, (anziché k come sarebbe per una successione) ci dice che il dominio è
una successione crescente di interi e la tabella che rappresenta la funzione ha 3 righe:
gli indici, i valori del dominio e i valori del codominio.
Se si vogliono valutare i tassi di variazione, le sole differenze dei valori
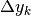 non bastano, perché vanno valutate in rapporto alle differenze
non bastano, perché vanno valutate in rapporto alle differenze
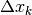 che sono relative ad esse. Graficamente: la diversa altezza delle colonne nel grafico va considerata in rapporto alle diverse basi.
Per esempio
che sono relative ad esse. Graficamente: la diversa altezza delle colonne nel grafico va considerata in rapporto alle diverse basi.
Per esempio 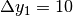 e
e 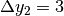 , ma la prima differenza dà luogo
ad un tasso di variazione minore, perché va rapportata alla differenza
, ma la prima differenza dà luogo
ad un tasso di variazione minore, perché va rapportata alla differenza 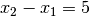 , mentre
, mentre 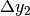 si mette in rapporto con
si mette in rapporto con 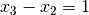 .
.
Il rapporto fra le differenze è proprio il calcolo che consente di ottenere il tasso
di variazione ed è un calcolo così importante da meritare un nome specifico: rapporto incrementale e una scrittura particolare: 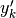 .
In pratica il risultato si ottiene calcolando
.
In pratica il risultato si ottiene calcolando 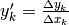 .
.
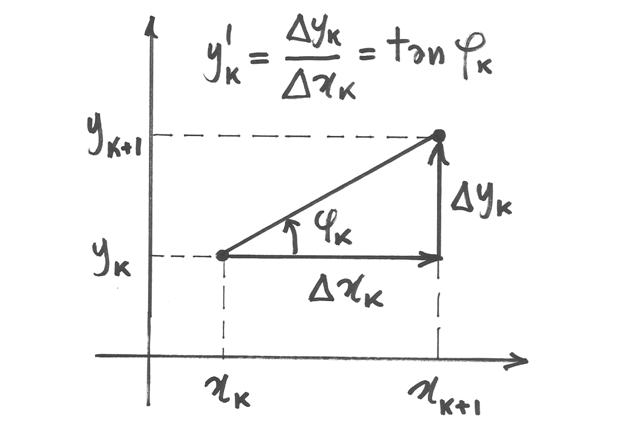
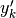 si dice rapporto incrementale relativo all’indice k. Analogamente alla differenza nelle
successioni, il rapporto incrementale graficamente
corrisponde alla pendenza del segmento che unisce il punto di ordinata a
si dice rapporto incrementale relativo all’indice k. Analogamente alla differenza nelle
successioni, il rapporto incrementale graficamente
corrisponde alla pendenza del segmento che unisce il punto di ordinata a 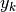 con quello
di ordinata a
con quello
di ordinata a 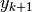 .
.
Un esempio¶
Immaginiamo 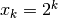 e
e 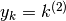 per
per 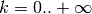 e calcoliamo
e calcoliamo 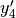 .
.
- Calcolo diretto:
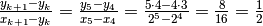
- Dal generale al particolare:
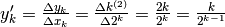 .
La formula generale consente il calcolo di qualsiasi differenza, quindi,
per k=4 si ha
.
La formula generale consente il calcolo di qualsiasi differenza, quindi,
per k=4 si ha 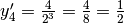 .
.
Si noti che nel secondo caso 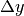 si calcola sulla base di quanto visto a proposito delle differenze.
si calcola sulla base di quanto visto a proposito delle differenze.
Regole di calcolo del rapporto incrementale¶
Siamo quindi ad un punto importante, che vale come regola generale: il rapporto incrementale nelle
funzioni a dominio discreto si calcola utilizzando le formule dei capitoli precedenti e dividendole
per 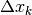 . Dalle stesse formule derivano le regole seguenti:
. Dalle stesse formule derivano le regole seguenti:
Rapporto incrementale in funzioni a dominio continuo¶
Nelle successioni e in generale nelle funzioni a dominio discreto l’incremento si calcola variando
l’indice k: 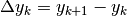 . Nelle funzioni a dominio continuo l’indice non esiste
e quindi non c’è un intervallo prestabilito della variabile per calcolare l’incremento della funzione.
Chiamando
. Nelle funzioni a dominio continuo l’indice non esiste
e quindi non c’è un intervallo prestabilito della variabile per calcolare l’incremento della funzione.
Chiamando 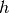 l’incremento della variabile
l’incremento della variabile 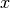 possiamo dare la seguente definizione.
possiamo dare la seguente definizione.
Sia 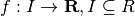 , definiamo l’incremento di f relativo al punto x
e all’incremento h:
, definiamo l’incremento di f relativo al punto x
e all’incremento h: 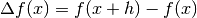 , con
, con 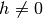 .
.
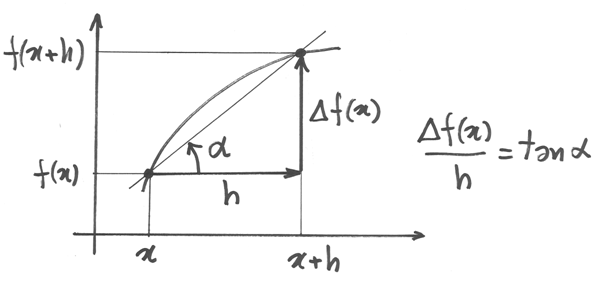
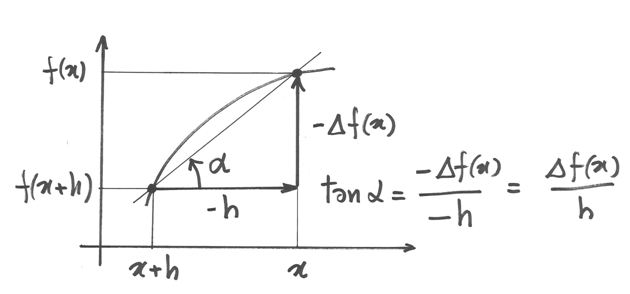
Possiamo così definire anche il rapporto incrementale della funzione, relativo al punto x e
all’incremento h: 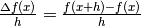 . Il rapporto ha il significato geometrico della pendenza della retta che passa per i punti
. Il rapporto ha il significato geometrico della pendenza della retta che passa per i punti 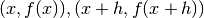 ed è il tasso medio di variazione della funzione fra i due punti.
ed è il tasso medio di variazione della funzione fra i due punti.
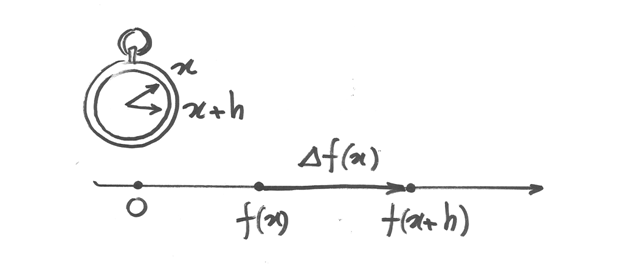
Possiamo pensare ad un’analogia cinematica, se interpretiamo 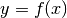 come la posizione all’istante
come la posizione all’istante 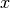 di un punto che si muove su una
retta, allora la differenza
di un punto che si muove su una
retta, allora la differenza 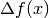 rappresenta lo spostamento del
punto fra l’istante
rappresenta lo spostamento del
punto fra l’istante 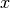 e l’istante
e l’istante 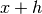 e il rapporto incrementale
e il rapporto incrementale
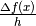 rappresenta la velocità media relativa all’istante
rappresenta la velocità media relativa all’istante
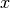 e alla durata
e alla durata 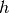 .
.
Note
La definizione di rapporto incrementale vale anche se l’incremento è 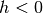 . In questo caso per
la differenza di f(x) si ha
. In questo caso per
la differenza di f(x) si ha 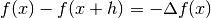 . E per la differenza di x:
. E per la differenza di x:
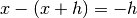 . Per cui il rapporto incrementale è
. Per cui il rapporto incrementale è 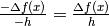 .
.
Rapporto incrementale di funzioni note¶
Funzione identica¶
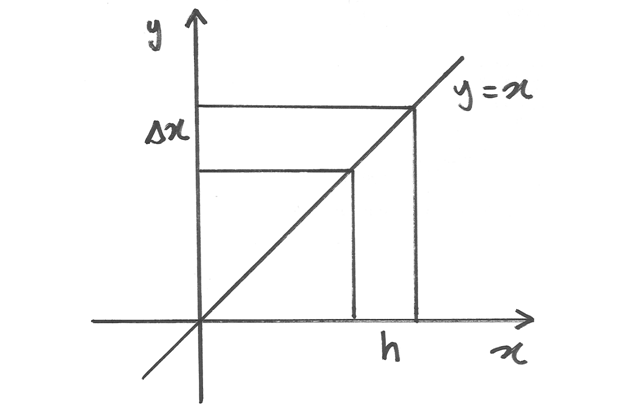
Se 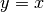 allora
allora 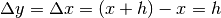 , cioè l’incremento della
funzione è uguale all’incremento della variabile, quindi il loro rapporto vale 1.
Come si vede anche dal grafico, il rapporto incrementale è il coefficiente angolare del segmento
che unisce i due punti, che in questo caso non è secante al grafico della funzione, ma gli appartiene.
, cioè l’incremento della
funzione è uguale all’incremento della variabile, quindi il loro rapporto vale 1.
Come si vede anche dal grafico, il rapporto incrementale è il coefficiente angolare del segmento
che unisce i due punti, che in questo caso non è secante al grafico della funzione, ma gli appartiene.
Il fatto che 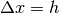 ci permette di usare d’ora in poi
ci permette di usare d’ora in poi 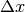 al posto di h
al posto di h
Funzione quadratica¶
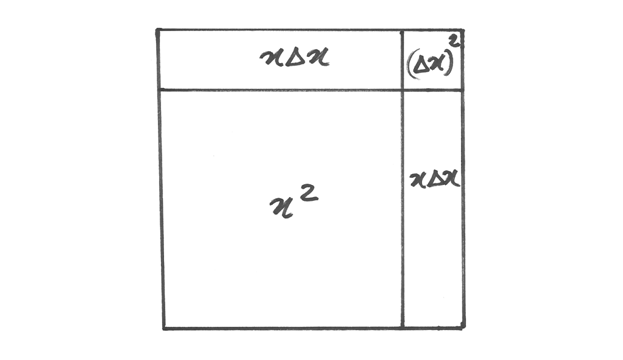
Se 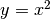 , allora
, allora 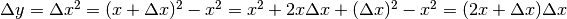 . Il disegno illustra le tre parti di cui si compone l’incremento di area
di un quadrato, analogamente a quanto già visto per
. Il disegno illustra le tre parti di cui si compone l’incremento di area
di un quadrato, analogamente a quanto già visto per 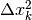 . Di conseguenza:
. Di conseguenza:
Note
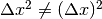 !!
!!
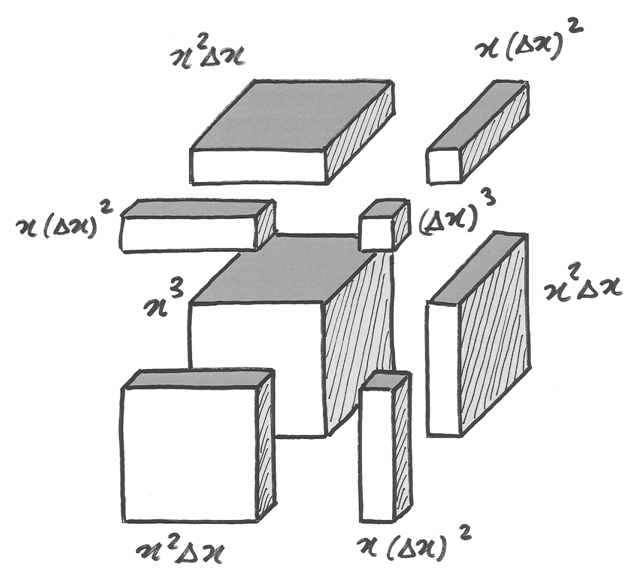
Funzione cubica¶
Con la stessa tecnica e aiutandosi con il disegno che si riferisce all’incremento di volume di un cubo,
si può calcolare 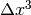 e il relativo rapporto incrementale.
e il relativo rapporto incrementale.
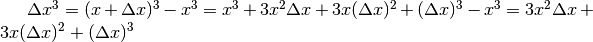 . Si ha così rapporto il incrementale :
. Si ha così rapporto il incrementale :
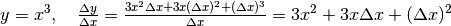 .
.
Funzione radice quadrata¶
Dalla definizione di differenza: 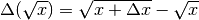 , da cui è facile ricavare il rappporto incrementale. Tuttavia più avanti ci sarà utile riscrivere la differenza come una frazione da razionalizzare:
, da cui è facile ricavare il rappporto incrementale. Tuttavia più avanti ci sarà utile riscrivere la differenza come una frazione da razionalizzare:
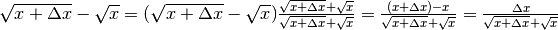 .
Da qui segue:
.
Da qui segue:
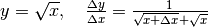 .
.
Funzione seno¶
Immaginando che x e 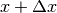 , con
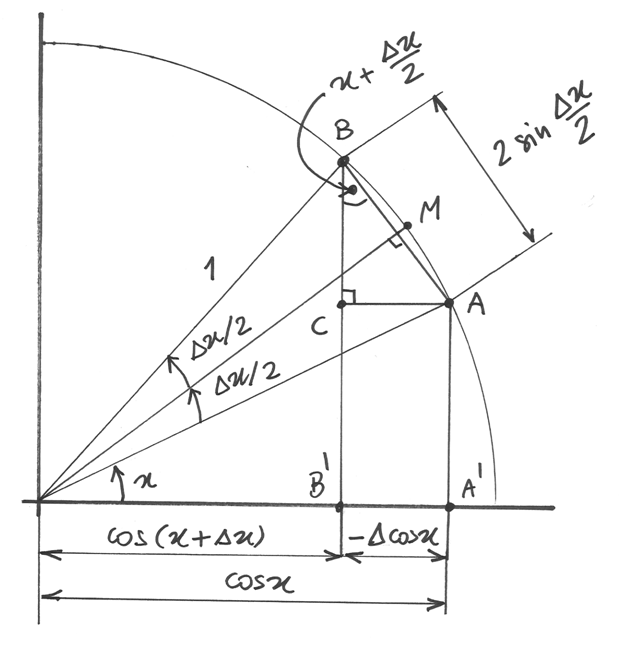
, con 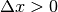 , siano angoli del primo quadrante, si consideri nel disegno il triangolo rettangolo ABC. L’angolo acuto in B è congruente con l’angolo
, siano angoli del primo quadrante, si consideri nel disegno il triangolo rettangolo ABC. L’angolo acuto in B è congruente con l’angolo
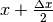 , perché i suoi lati AB e BC sono perpendicolari a OM e OA’.
Quindi
, perché i suoi lati AB e BC sono perpendicolari a OM e OA’.
Quindi 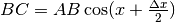 . Ma le due metà di AB valgono ciascuna
. Ma le due metà di AB valgono ciascuna 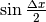 , e BC = BB’-AA’
, e BC = BB’-AA’ 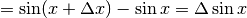 , quindi in conclusione:
, quindi in conclusione:
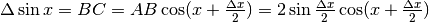 . Per cui il rapporto incrementale sarà:
. Per cui il rapporto incrementale sarà:
Funzione coseno¶
Per la dimostrazione si fa riferimento ad una figura analoga alla precedente, tenendo conto però
che questa volta il segmento che interessa è il lato AC = A’B’. La sua misura è 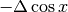 e, pur essendo nel primo qudrante, è una misura negativa perché
e, pur essendo nel primo qudrante, è una misura negativa perché 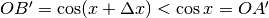 . Abbiamo che
. Abbiamo che 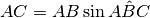 . Riferendoci anche ai calcoli fatti per il seno per ricavare AB, alla fine vediamo che
. Riferendoci anche ai calcoli fatti per il seno per ricavare AB, alla fine vediamo che 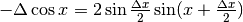 , da cui
, da cui
Note
Per dimostrare la formula della differenza per il seno e per il coseno anche con x e 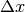 negativi, si sviluppa la definizione di differenza e si usano le formule di prostaferesi.
negativi, si sviluppa la definizione di differenza e si usano le formule di prostaferesi.
Regole di calcolo del rapporto incrementale¶
Ricordando le regole già viste per le funzioni a dominio discreto, abbiamo le regole di calcolo seguenti:
Esercizi svolti¶
Calcoli diretti¶
Si risolvono con la calcolatrice senza fare uso delle formule.
Calcolare
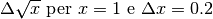 .
.Basta esplicitare le definizione
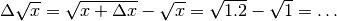
Calcolare
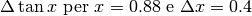 .
.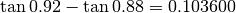
I calcoli diretti sono sempre possibili se le funzioni coinvolte si trovano sulla calcolatrice. Non essendoci dati incogniti, è facile anche calcolare il rapporto incrementale.
Problema 1¶
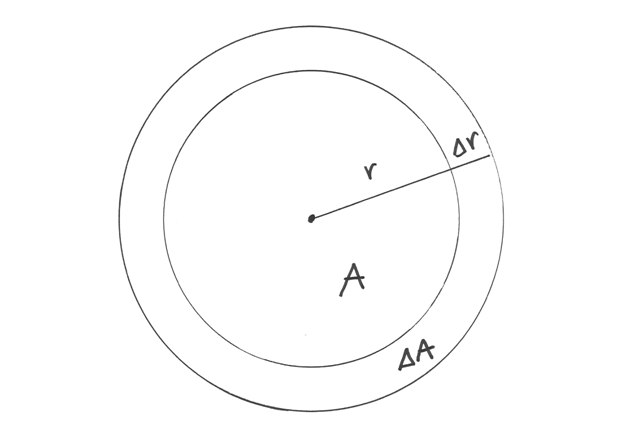
Un cerchio di raggio 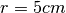 viene ingrandito fino a che la sua area aumenta di
viene ingrandito fino a che la sua area aumenta di 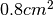 .
Di quanto aumenta il suo raggio?
.
Di quanto aumenta il suo raggio?
Mettiamo in relazione l’area e il raggio e calcoliamo le differenze. La funzione è 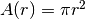 .
La sua differenza è
.
La sua differenza è ![\Delta A(r)=\Delta (\pi r^2)= \pi\Delta r^2=\pi[2r\Delta r+(\Delta r)^2]](../../../_images/math/4a9d90c34f232dc6ec7b0261fb23703775a5f202.png) .
Cioé:
.
Cioé: 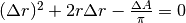
Inserendo i dati diventa 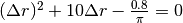 , che è un’equazione di secondo
grado nell’incognita
, che è un’equazione di secondo
grado nell’incognita 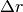 . Consideriamo solo la soluzione positiva e troviamo con l’aiuto della calcolatrice:
. Consideriamo solo la soluzione positiva e troviamo con l’aiuto della calcolatrice:
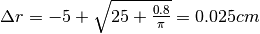
Si tratta di un problema tipico, cioé di un problema nel quale viene fornito il valore di 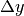 e viene richiesto di calcolare
e viene richiesto di calcolare 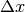 tramite l’equazione
tramite l’equazione 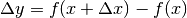 .
Nel problema proposto la soluzione è semplice, ma non lo è in generale e per raggiungerla occorre fare
ricorso a tecniche di approssimazione che saranno spiegate più avanti.
.
Nel problema proposto la soluzione è semplice, ma non lo è in generale e per raggiungerla occorre fare
ricorso a tecniche di approssimazione che saranno spiegate più avanti.
Problema 2¶
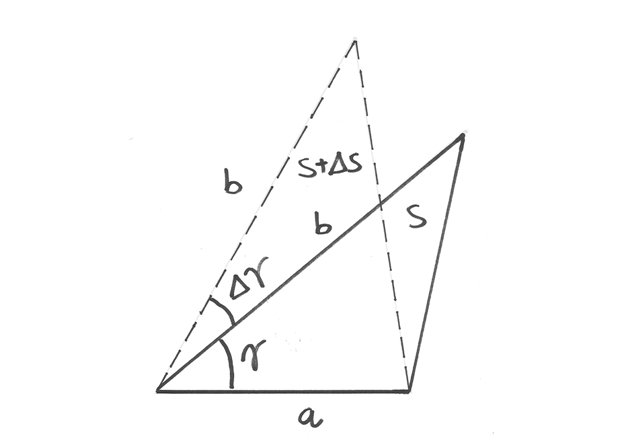
Si vuole aumentare di 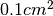 la superficie di un triangolo con i lati a=5cm, b =8cm,
angolo compreso
la superficie di un triangolo con i lati a=5cm, b =8cm,
angolo compreso 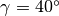 . Di quanto deve aumentare l’angolo
. Di quanto deve aumentare l’angolo 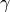 ?
?
Anche in questo problema c’è una formula diretta che lega l’area all’angolo:
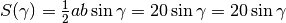 . Utilizzando le regole note per le differenze, ricaviamo:
. Utilizzando le regole note per le differenze, ricaviamo: ![\Delta S=\Delta(20\sin\gamma)=20[\sin(\gamma + \Delta \gamma)-sin\gamma]](../../../_images/math/68feac866672f76f6b1d3e96bab5b47da82fa50b.png)
Inserendo i dati, l’equazione diventa:
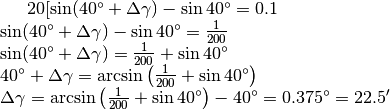
La formula generale è 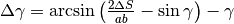 .
.
L’esistenza della formula che lega direttamente le due variabili
facilita enormemente la soluzione, che altrimenti richiederebbe tecniche molto più sofisticate.
Ripetiamo infatti che se l’equazione è 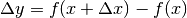 non è per nulla scontato risalire
al valore utile
non è per nulla scontato risalire
al valore utile 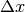 a partire dal valore conosciuto di
a partire dal valore conosciuto di 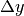 .
.
Riassunto¶
- Il rapporto incrementale serve a calcolare il tasso di variazione della funzione fra due suoi valori.
- Graficamente corrisponde alla pendenza del segmento che unisce i due punti
di ascissa x e
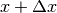 .
. - Il rapporto incrementale si calcola come rapporto fra l’incremento della funzione e l’incremento della variabile e ha due formulazioni diverse se la funzione è a dominio continuo o a dominio discreto.
- Dopo avere imparato a calcolare questo rapporto nel caso di funzioni elementari, per passare a funzioni composte occorre conoscere le regole che consentono di applicare il rapporto incrementale a somme, prodotti, quozienti ecc.
- La tecnica di calcolare le differenze è immediatamente risolutiva nei problemi in cui una formula fornisce il legame diretto fra due variabili.
Esercizi¶
#. Ricava algebricamente le regole di calcolo del rapporto incrementale nelle fu nzioni a dominio discreto,
partendo dalla definizione di rapporto incrementale e utilizzando le formule sulle differenze.
- Spiega la nota del paragrafo 5.5.2, chiarendo perché se
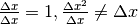
- Verifica che
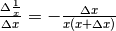
- Verifica che
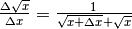
- Verifica che
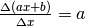
- Segui i suggerimenti della nota al paragrafo 5.5.5 e dimostra le formule delle differenze per il seno e per il coseno.
- Calcolare
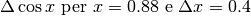
- Calcolare
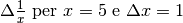
- Calcolare
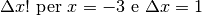
- Un rombo ha una diagonale di 10 cm. Di quanto occorre allungare l’altra diagonale perché la sua
superficie aumenti di 0.2
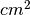 ?
? - Un triangolo equilatero ha l’altezza di 10 cm. Di quanto occorre allungarla perché il suo perimetro aumenti di 8 cm?
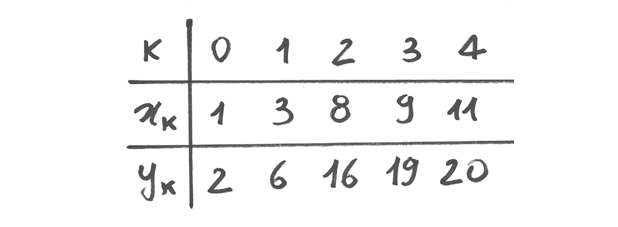
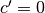
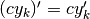
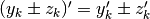
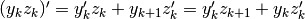
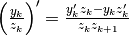
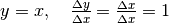
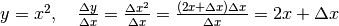
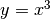
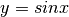
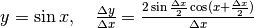
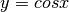
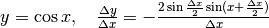
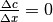
![\frac{\Delta [cf(x)]}{\Delta x} =c\frac{\Delta f(x)}{\Delta x}](../../../_images/math/bc08ab2a6f91a3d850a3d6936773fc7fd812123e.png)
![\frac{\Delta [f(x) \pm g(x)]}{\Delta x} =\frac{\Delta f(x)}{\Delta x} \pm \frac{\Delta g(x)}{\Delta x}](../../../_images/math/d4807d37dc8ffdeaeec4592a32b50858b58b33f3.png)
![\frac{\Delta [f(x)g(x)]}{\Delta x} = \frac{\Delta f(x)}{\Delta x}g(x)+f(x+\Delta x)\frac{\Delta g(x)}{\Delta x} = \\ = \frac{\Delta f(x)}{\Delta x}g(x+\Delta x)+f(x)\frac{\Delta g(x)}{\Delta x} \\ = \frac{\Delta f(x)}{\Delta x}g(x)+f(x)\frac{\Delta g(x)}{\Delta x}+\frac{\Delta f(x)}{\Delta x}\frac{\Delta g(x)}{\Delta x}\Delta x](../../../_images/math/49fe7309491a902ae6f3629148dea01c1ab5cb14.png)
![\frac{\Delta \left[\frac {f(x)}{g(x)}\right]}{\Delta x} =\frac{\frac{\Delta f(x)}{\Delta x}g(x)-f(x)\frac{\Delta g(x)}{\Delta(x)}}{g(x)g(x+\Delta x)}](../../../_images/math/34bd852fd4031f90687a54fde6e12b8836589356.png)