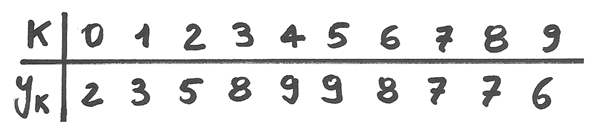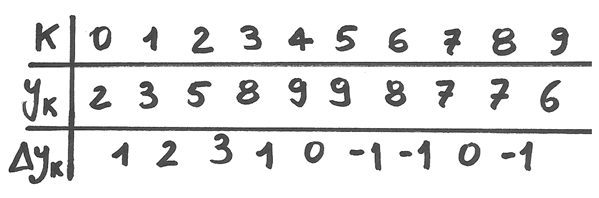Le successioni e le differenze¶
Funzioni a dominio discreto e successioni¶
Una funzione a dominio discreto 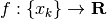 è una funzione il cui dominio è un insieme di valori distinti,
che la variabile x assume senza variare con continuità fra l’uno e l’altro.
In generale i valori di tale funzione (e quindi il codominio) saranno numeri reali.
Il suo grafico nel piano cartesiano è dato da punti distinti
è una funzione il cui dominio è un insieme di valori distinti,
che la variabile x assume senza variare con continuità fra l’uno e l’altro.
In generale i valori di tale funzione (e quindi il codominio) saranno numeri reali.
Il suo grafico nel piano cartesiano è dato da punti distinti 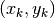 dove
dove
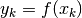 .
.
Le successioni sono particolari funzioni a dominio discreto, nel senso che il loro dominio
è dato dagli indici, che formano un intervallo anche infinito di numeri interi.
I punti dei loro grafici avranno quindi coordinate 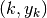 e saranno distribuiti con regolarità, perché la distanza orizzontale fra l’uno e l’altro
è unitaria: corrisponde alla differenza fra due indici consecutivi.
e saranno distribuiti con regolarità, perché la distanza orizzontale fra l’uno e l’altro
è unitaria: corrisponde alla differenza fra due indici consecutivi.
Una successione (e in generale una funzione a dominio discreto) 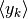 si indica
in modo diverso dall’insieme
si indica
in modo diverso dall’insieme 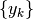 dei suoi valori.
Per distinguere i due significati, consideriamo le due successioni
dei suoi valori.
Per distinguere i due significati, consideriamo le due successioni
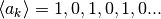 e
e
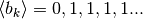 : sono generate da regole diverse ma
hanno lo stesso insieme di valori
: sono generate da regole diverse ma
hanno lo stesso insieme di valori 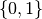 .
.
Le due regole sono: 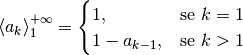 e
e 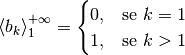
Differenze e tasso di variazione¶
Nella tabella consideriamo una successione 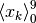 , i cui 10 termini crescono da 2 fino a 9 e poi calano a 6.
Si possono valutare le differenze fra un termine e il successivo con facili sottrazioni.
Le differenze sono espresse nella terza riga della prossima tabella , dove si vede che per ogni k
, i cui 10 termini crescono da 2 fino a 9 e poi calano a 6.
Si possono valutare le differenze fra un termine e il successivo con facili sottrazioni.
Le differenze sono espresse nella terza riga della prossima tabella , dove si vede che per ogni k 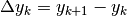 , cioè la differenza relativa al termine k-esimo
si calcola partendo dal termine successivo.
, cioè la differenza relativa al termine k-esimo
si calcola partendo dal termine successivo.
In questo modo si noti che se la successione non ha infiniti termini, il numero delle differenze è uno di meno rispetto al numero dei termini.
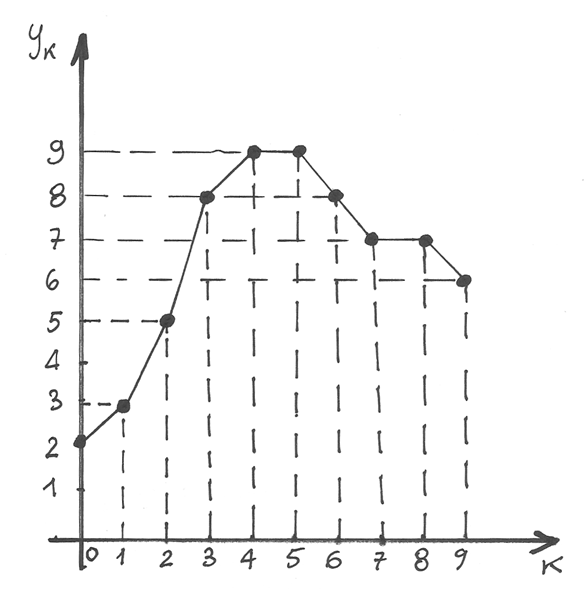
L’andamento dei termini può essere visualizzato da un semplice grafico:
Le le osservazioni importanti sul grafico sono due:
- La linea spezzata che unisce i punti è disegnata per pura comodità di lettura, ma non dovrebbe esserci, perché la successione non ha valori da rappresentare fra i punti disegnati
- Le colonne hanno pari larghezza (la base delle colonne misura 1) e per questo le differenze
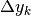 corrispondono al tasso di variazione fra un punto e l’altro.
corrispondono al tasso di variazione fra un punto e l’altro.
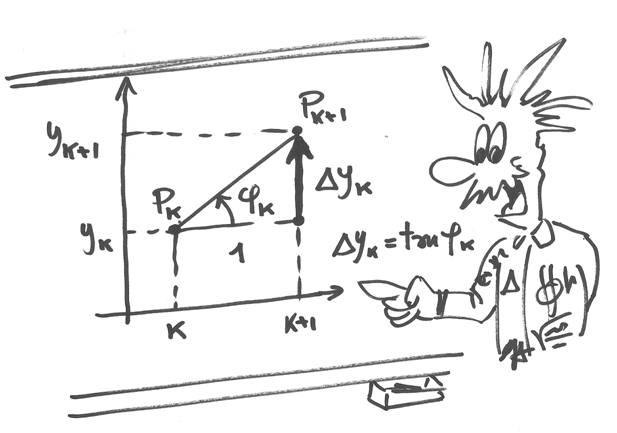
Come vedremo in seguito, nel caso generale di una funzione a dominio discreto
il tasso di variazione non si calcola con la semplice differenza 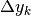 , mentre questo
calcolo è sufficiente per le successioni. Lo si può vedere dal grafico: infatti qui le colonne
hanno uguale base e quindi solo la loro differente altezza influisce sulla pendenza del segmento
che unisce due punti consecutivi, nel senso che un
, mentre questo
calcolo è sufficiente per le successioni. Lo si può vedere dal grafico: infatti qui le colonne
hanno uguale base e quindi solo la loro differente altezza influisce sulla pendenza del segmento
che unisce due punti consecutivi, nel senso che un 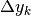 maggiore produce
inevitabilmente una pendenza maggiore. La pendenza è l’equivalente grafico del tasso di variazione.
maggiore produce
inevitabilmente una pendenza maggiore. La pendenza è l’equivalente grafico del tasso di variazione.
I fattoriali decrescenti¶
Alcune utili regole sui rapporti incrementali discendono dall’utilizzo di un particolare tipo di prodotto fattoriale.
Sappiamo già che il fattoriale di n è 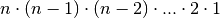 , cioè il prodotto di un numero per tutti i suoi precedenti.
Si può limitare il prodotto a p fattori. Allora la nuova funzione si chiama fattoriale
decrescente di ordine p del numero k:
, cioè il prodotto di un numero per tutti i suoi precedenti.
Si può limitare il prodotto a p fattori. Allora la nuova funzione si chiama fattoriale
decrescente di ordine p del numero k: 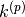 . Ecco alcuni esempi
. Ecco alcuni esempi
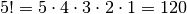 , ma:
, ma: 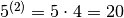 .
.
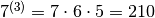 , ma
, ma 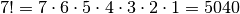
Quindi, in generale: 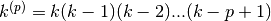 . Per avere almeno due fattori, si intende generalmente
p>1, ma è possibile ricavare il risultato anche in situazioni meno ovvie.
. Per avere almeno due fattori, si intende generalmente
p>1, ma è possibile ricavare il risultato anche in situazioni meno ovvie.
Prima di tutto è ovvio che p non è un esponente. È chiaro anche che se p=k, allora 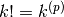 e se invece p>k allora risultato è nullo.
e se invece p>k allora risultato è nullo.
Ricaviamo una formula. Poniamo k=10 e p=3.
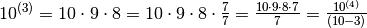 .
Da questo esempio e da altri calcoli analoghi che puoi sviluppare per esercizio,
si intuisce che vale una regola importante:
.
Da questo esempio e da altri calcoli analoghi che puoi sviluppare per esercizio,
si intuisce che vale una regola importante: 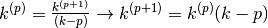 .
.
Se applichiamo la regola a 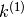 ricaviamo
ricaviamo 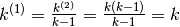 .
In modo facile si può verificare anche
.
In modo facile si può verificare anche 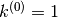
Quanto a k, se k è un intero negativo, la regola non cambia. Esempio:
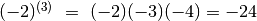
Un esempio per k razionale: 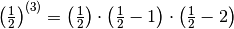
Calcoli di differenze¶
Differenze per la successione quadratica¶
Della successione: 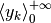 , con
, con 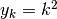 (oppure,
che è lo stesso, della successione
(oppure,
che è lo stesso, della successione 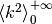 )
calcoliamo la decima differenza
)
calcoliamo la decima differenza 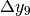 . Ci sono due modi, quello che risolve
il caso particolare e quello che scrive prima la formula generale e poi la applica.
. Ci sono due modi, quello che risolve
il caso particolare e quello che scrive prima la formula generale e poi la applica.
, oppure
che nel caso specifico vale
.
Il secondo modo è più significativo, perché indica una regola generale: la differenza fra due quadrati consecutivi è il successivo del doppio del primo ed è sempre dispari.
Differenze per la successione dei reciproci¶
Calcoliamo la formula generale di 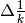 e verifichiamo il risultato per k=8.
e verifichiamo il risultato per k=8.
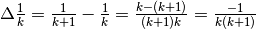 che se k=8 risulta
che se k=8 risulta 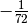
Per via diretta si verifica il risultato facilmente. Le differenze della successione dei reciproci saranno tutte negative, dato che 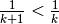
Differenze di fattoriali decrescenti¶
Riassumiamo i calcoli e gli esempi per capire come si comportano le differenze nelle successioni dei fattoriali decrescenti:
| p | 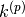 |
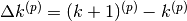 |
|---|---|---|
| 0 | 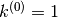 |
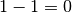 |
| 1 | 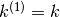 |
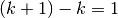 |
| 2 | 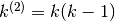 |
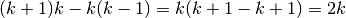 |
| 3 | 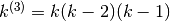 |
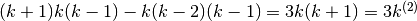 |
| ... | ... | ... |
| p | 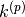 |
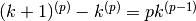 |
L’ultima formula della tabella ci dà quindi la regola: 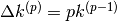
Differenze nelle progressioni geometriche¶
Fissiamo come primo esempio la progressione di ragione 2: 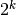 .
.
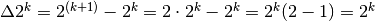
Il termine generale della progressione esprime quindi anche le sue differenze. Vediamo ora
altre successioni con termini esponenziali  e le loro differenze.
e le loro differenze.
Riassumendo¶
- Le successioni e le funzioni a dominio discreto sono funzioni a valori distinti e il loro grafico è una successione di punti nel piano cartesiano.
- I segmenti che li uniscono hanno una pendenza che corrisponde al tasso di
variazione, un numero che si calcola attraverso una nuova funzione:
il cosiddetto rapporto incrementale
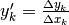 .
. - Diamo una sintesi dei casi notevoli di
 |
 |
|---|---|
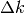 |
1 |
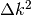 |
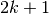 |
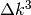 |
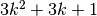 |
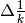 |
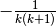 |
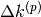 |
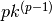 |
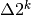 |
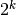 |
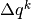 |
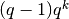 |
Esercizi¶
- Calcola le differenze
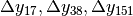 della successione
della successione
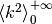 .
. - Calcola nei due modi la differenza
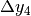 della successione
della successione
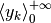 con
con 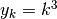 .
. - Calcola la quinta differenza della successione dei numeri pari. È un risultato particolare o generale?
- Calcola la formula generale di
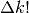
- Trova i risultati per due fattoriali decrescenti a tuo piacere: se k è un intero negativo e se k è un razionale qualsiasi.
- Giustifica la regola dei fattoriali decrescenti esplicitando la formula.
- Mediante la stessa regola calcola
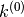
- Estendi a indici negativi i fattoriali decrescenti. Calcolando
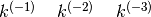 giustifica la formula generale
giustifica la formula generale 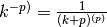 (p si intende positivo).
(p si intende positivo). - Aggiungi alcune righe alla tabella dei fattoriali decrescenti e calcola le differenze
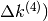 e
e 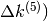 in modo da giustificare la formula generale.
in modo da giustificare la formula generale. - Fissa successivamente k= -4, -3, -2, -1, 0, 1, 2, ... e calcola i valori
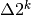 .
.