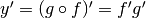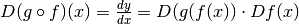Funzioni composte e funzioni inverse¶
Derivata come coefficiente di dilatazione¶
L’equazione 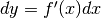 , esatta a meno di infinitesimi di ordine superiore,
può essere interpretata in un nuovo modo. Se
, esatta a meno di infinitesimi di ordine superiore,
può essere interpretata in un nuovo modo. Se 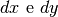 si
intendono come segmenti infinitesimi, allora
si
intendono come segmenti infinitesimi, allora 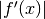 è il coefficiente
che trasforma la misura
è il coefficiente
che trasforma la misura 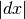 nella misura
nella misura 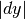 . Per esempio, se la
derivata vale 2 (
. Per esempio, se la
derivata vale 2 (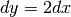 ), una variazione infinitesima di x si
riflette in una variazione doppia di y. Il segno della derivata ci
dice se l’orientamento dei due segmenti infinitesimi è concorde o discorde.
Per esempio, l’espressione
), una variazione infinitesima di x si
riflette in una variazione doppia di y. Il segno della derivata ci
dice se l’orientamento dei due segmenti infinitesimi è concorde o discorde.
Per esempio, l’espressione 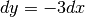 mostra che la variazione infinitesima
di x produce una variazione tripla di y, ma di segno opposto: se x cresce,
y decresce di tre volte tanto.
mostra che la variazione infinitesima
di x produce una variazione tripla di y, ma di segno opposto: se x cresce,
y decresce di tre volte tanto.
Funzione di funzione e sua derivata¶
Immaginiamo di avere una funzione f(x), definita su un intervallo 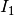 ,
,
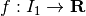 che trasforma x in u=f(x), e un’altra funzione
che trasforma x in u=f(x), e un’altra funzione
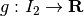 , con
, con 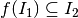 che trasforma
u in y=f(u). Le due funzioni si possono comporre, cioé applicare successivamente
l’una ai valori dell’altra in modo che la loro composizione
che trasforma
u in y=f(u). Le due funzioni si possono comporre, cioé applicare successivamente
l’una ai valori dell’altra in modo che la loro composizione 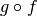 trasformi
trasformi
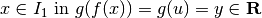 . Se f è derivabile in x,
per esempio con
. Se f è derivabile in x,
per esempio con 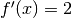 , e g è derivabile in u=f(x), per esempio
, e g è derivabile in u=f(x), per esempio
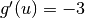 , vuol dire che ad un incremento infinitesimo dx corrisponde
un incremento doppio du=2dx e che a questo incremento infinitesimo du corrisponde
un incremento triplo, ma di segno opposto, dy=-3du=-3(2dx) . Sicché alla fine
l’incremento infinitesimo è dy=-6dx.
, vuol dire che ad un incremento infinitesimo dx corrisponde
un incremento doppio du=2dx e che a questo incremento infinitesimo du corrisponde
un incremento triplo, ma di segno opposto, dy=-3du=-3(2dx) . Sicché alla fine
l’incremento infinitesimo è dy=-6dx.
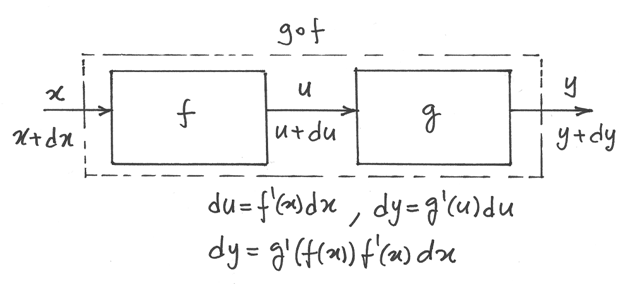
Il disegno mette i valori x del dominio di f sull’asse verticale verso il basso. Quei valori u=f(x) che fanno parte del codominio di f e che costituiscono il dominio di g sono sull’asse orizzontale. Grazie ai microscopi si può seguire il percorso che trasforma la variazione infinitesima dx nella variazione finale dy=-6dx attraverso il passaggio intermedio du=2dx .
La funzione f si deriva nel punto x, mentre la funzione g si deriva nel punto u=f(x).
Abbiamo dy=g’(u)du e du=f’(x)dx, quindi dy=g’(u)f’(x)dx. In pratica la derivata della composizione di due funzioni è il prodotto delle due derivate.
La regola è importantissima e di uso assai frequente.
Esempi¶
- Derivare
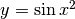 .
In questo esempio
.
In questo esempio 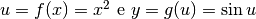 .
.
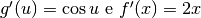 , quindi
, quindi
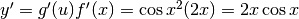 .
. - Derivare
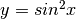 .
Questa volta
.
Questa volta 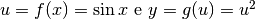 .
.
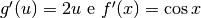 , ne risulta
, ne risulta
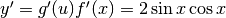 .
.
Nota. Evidentemente 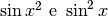 sono funzioni diverse.
sono funzioni diverse.
Derivare
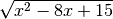 .
.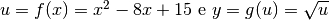 .
.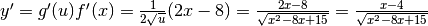 .
.Derivare
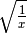 .
Sappiamo già svolgere questa derivata, con la regola delle potenze:
.
Sappiamo già svolgere questa derivata, con la regola delle potenze: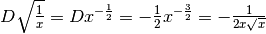 .
.
La regola delle funzioni composte può essere usata anche in questo caso, anche
se è meno conveniente: 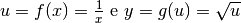 .
.
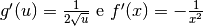 , quindi
, quindi 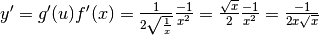 .
.
Derivare la composizione di più funzioni¶
La regola non cambia se la funzione si compone di più di due funzioni.
Con 3 funzioni: sia 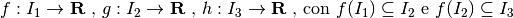 .
Allora esiste la funzione
.
Allora esiste la funzione 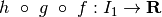 , tale che
, tale che
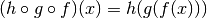 . Dato un
. Dato un 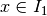 , se u=f(x), v=g(u), y=h(v) e se queste funzioni sono derivabili, allora in corrispondenza di un incremento
infinitesimo dx , le funzioni f, g, h subiranno gli incrementi du=f’(x)dx, dv=g’(f(x))du,
dy=h(g(f(x)))dv e quindi
, se u=f(x), v=g(u), y=h(v) e se queste funzioni sono derivabili, allora in corrispondenza di un incremento
infinitesimo dx , le funzioni f, g, h subiranno gli incrementi du=f’(x)dx, dv=g’(f(x))du,
dy=h(g(f(x)))dv e quindi 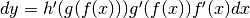 per cui vale ancora la regola del prodotto delle derivate
per cui vale ancora la regola del prodotto delle derivate
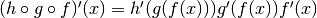 .
.
Esempio¶
Derivare
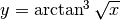 .
Le tre funzioni sono
.
Le tre funzioni sono
 .
Quindi:
.
Quindi: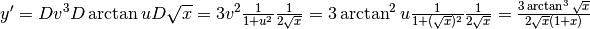 .
.
Problemi¶
1. Gonfiare il pallone¶
Un pallone inizialmente sgonfio, viene gonfiato al ritmo di un litro al secondo. Con quale velocità sta aumentando la sua superficie dopo 5 secondi?
Poiché 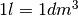 , il volume del pallone cresce ogni secondo di
, il volume del pallone cresce ogni secondo di 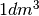 e la funzione che rappresenta il volume è
e la funzione che rappresenta il volume è 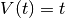 . Per una sfera
. Per una sfera
![V=\frac{4}{3}\pi r^3 \mbox{ da cui }r=\sqrt[3]{\frac{3V}{4\pi}}](../../../_images/math/a32c231a21ba7bbe497631faff2daec1b79ca580.png) . La superficie
dipende dal raggio:
. La superficie
dipende dal raggio: 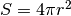 e sostituendo r si ha:
e sostituendo r si ha:
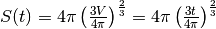 .
Per sapere la velocità di espansione della superficie al quinto secondo
occorre calcolare S’(5). Calcoliamo prima la derivata e poi poniamo t=5 .
.
Per sapere la velocità di espansione della superficie al quinto secondo
occorre calcolare S’(5). Calcoliamo prima la derivata e poi poniamo t=5 .
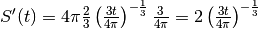 .
Per t=5 abbiamo:
.
Per t=5 abbiamo: 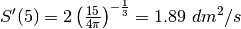 .
.
2. La distanza fra due treni¶
Un treno parte alle 8 del mattino e viaggia verso Est alla velocità di 90 km/h, mentre un altro treno parte alle 9 di mattina dallo stesso punto e viaggia verso Nord alla velocità di 120 km/h. A quale velocità si stanno allontanando i due treni a mezzogiorno?
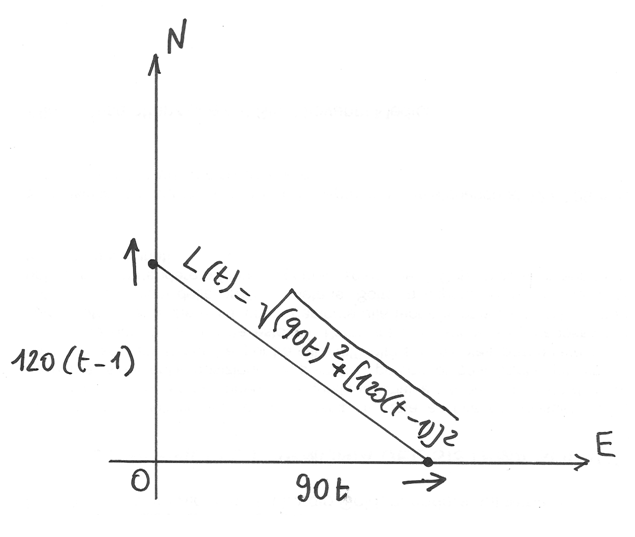
Rappresentiamo il moto dei due treni in un sistema di assi cartesiani, come nella figura.
Al tempo t il primo treno si trova sull’asse x alla posizione 90t, mentre
il secondo treno si trova sull’asse y alla posizione 120(t-1) perché parte un’ora
dopo il primo. La distanza fra i due treni è data dal Teorema di Pitagora:
![L(t)=\sqrt{(90t)^2+[120(t-1)]^2}](../../../_images/math/a8cdac155a8535e7840dd73ad2f0676cef985e0b.png) di questa funzione dobbiamo calcolare la
derivata rispetto al tempo e poi valutarla per t=4 (cioé 4 ore dopo la partenza).
di questa funzione dobbiamo calcolare la
derivata rispetto al tempo e poi valutarla per t=4 (cioé 4 ore dopo la partenza).
![L'(t)=\frac{8100\cdot 2t+14400\cdot 2(t-1)}{2\sqrt{8100t^2+14400(t-1)^2}}=\frac{900[9t+16(t-1)]}{30\sqrt{9t^2+16(t-1)^2}}=\frac{30(25t-16}{\sqrt{25t^2-32t+16}}](../../../_images/math/9594cc1bbace22c70d18b67c0428c020e4d38ea6.png) .
.
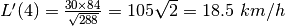 .
.
Derivare l’inversa di una funzione¶
Conosciamo già alcune regole di derivazione di funzioni inverse: per esempio delle radici, che sono inverse delle potenze. Ma non abbiamo individuato la regola che lega la derivata di una funzione alla derivata della sua inversa. È quello che stiamo per fare.
Sia 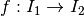 derivabile e invertibile. Esiste dunque la funzione inversa
derivabile e invertibile. Esiste dunque la funzione inversa 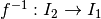 . In generale, il fatto che f sia derivabile
non ci assicura sull’esistenza della derivata di
. In generale, il fatto che f sia derivabile
non ci assicura sull’esistenza della derivata di 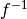 . Anzi,
. Anzi,
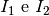 potrebbero anche essere disgiunti. Quindi, preso un x
di
potrebbero anche essere disgiunti. Quindi, preso un x
di 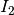 , non siamo certi che esista f(x) e quindi neanche f’(x) da
mettere in relazione con l’eventuale
, non siamo certi che esista f(x) e quindi neanche f’(x) da
mettere in relazione con l’eventuale 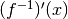 .
.
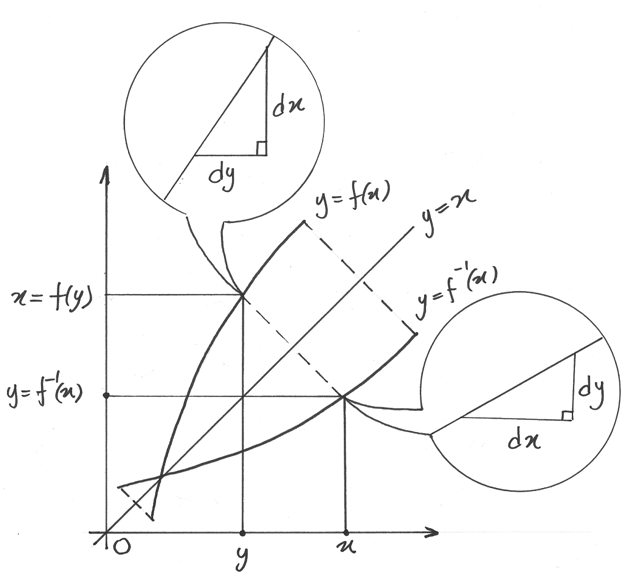
Il grafico della funzione e il grafico della sua inversa sono simmetrici rispetto
alla retta 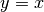 . Grazie a questa simmetria i punti
. Grazie a questa simmetria i punti 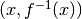 del grafico dell’inversa trovano corrispondenza nei punti
del grafico dell’inversa trovano corrispondenza nei punti 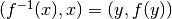 del grafico della funzione.
del grafico della funzione.
Se puntiamo i microscopi non standard su punti corrispondenti dei due grafici,
visualizziamo due segmenti che si corrispondono nella simmetria assiale 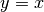 .
Se f è derivabile in
.
Se f è derivabile in 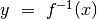 e la derivata è diversa da zero
(segmento non orizzontale), allora
e la derivata è diversa da zero
(segmento non orizzontale), allora 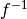 sarà derivabile in x (segmento
non verticale).
sarà derivabile in x (segmento
non verticale).
Consideriamo un incremento infinitesimo dx sul grafico della inversa, che provoca
un incremento 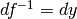 . Possiamo definire la derivata della funzione inversa
. Possiamo definire la derivata della funzione inversa 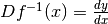 . Ora controlliamo i differenziali simmetrici
sul grafico della funzione f: si vede chiaramente che in ascissa e in ordinata
sono scambiati:
. Ora controlliamo i differenziali simmetrici
sul grafico della funzione f: si vede chiaramente che in ascissa e in ordinata
sono scambiati: 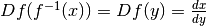 .
La regola è dunque questa: le due derivate sono reciproche una dell’altra:
.
La regola è dunque questa: le due derivate sono reciproche una dell’altra:
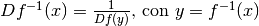 . Oppure:
. Oppure: 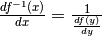 .
.
La derivata della funzione 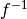 nel punto di ascissa x è il recipoco
della derivata della funzione f nel punto
nel punto di ascissa x è il recipoco
della derivata della funzione f nel punto 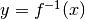 .
.
Esempi e esercizi svolti¶
- Calcolare
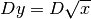 a partire da
a partire da 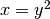 :
: 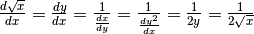 .
.
Ritroviamo quindi un risultato già noto e lo stesso vedremo nei prossimi esempi.
- Calcolare la derivata dell’arcotangente usando la formula dell’inversa.
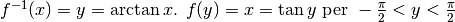 .
.
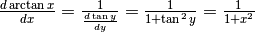 .
.
- Calcolare la derivata dell’arcoseno:
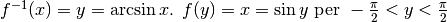 .
.
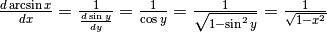 .
.
Nel trasformare 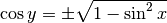 abbiamo scartato i valori negativi,
dato l’intervallo scelto per le y. Agli estremi di questo intervallo il denominatore
si annulla, quindi la derivata dell’arcoseno non esiste per
abbiamo scartato i valori negativi,
dato l’intervallo scelto per le y. Agli estremi di questo intervallo il denominatore
si annulla, quindi la derivata dell’arcoseno non esiste per 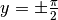 .
.
- Calcolare la derivata della radice ennesima:
![f^{-1}(x)=y=\sqrt[n]{x}\mbox{. }f(y)=x=y^n\ (x,y>0)](../../../_images/math/7293c2b0d595acd0d491bf98477a4dee1778120a.png) .
.
![\frac{d\sqrt[n]{x}}{dx}=\frac{1}{\frac{dy^n}{dy}}=\frac{1}{ny^{n-1}}=\frac{1}{n\sqrt[n]{x^{n-1}}}](../../../_images/math/bfb2ae8895d6f11eddfe59ec88b008c6fde7a203.png) .
.
Come si vede, la funzione non è derivabile per x=0. Anche questo risultato, come i prossimi, conferma quanto avevamo visto utilizzando la regola delle potenze.
- Calcolare
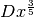 , con la regola delle funzioni inverse.
, con la regola delle funzioni inverse.
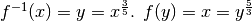 .
.
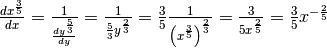 .
.
- Ricalcolare
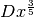 , con la regola delle funzioni composte.
, con la regola delle funzioni composte.
Pensiamo ![x^{\frac{3}{5}}=\sqrt[5]{x^3}](../../../_images/math/f6da190160751a6b22f228923dddf1cb41d3bd5e.png) . Allora
. Allora ![u=f(x)=x^3 \mbox{ e } y=g(u)=\sqrt[5]{u}](../../../_images/math/7291f10485317eaba15a3073da17f704bef7c2b2.png) .
.
![y'=g'(u)f'(x)= \frac{1}{5\sqrt[5]{u^4}}(3x^2)=\frac{3x^2}{5\sqrt[5]{\left(x^3\right)^4}}=\frac{3x^2}{5\sqrt[5]{x^{12}}}=\frac{3}{5\sqrt[5]{x^2}}=\frac{3}{5}x^{-\frac{2}{5}}](../../../_images/math/4ab0159926591dc70c678188a057dc4bbf062387.png) .
.
Come si vede, si deve utilizzare anche la regola della derivata dell’inversa per il calcolo della radice ennesima.
Resta il dubbio che la derivata sia calcolabile solo con alcuni esponenti razionali e non con tutti. In effetti nel Cap.7 abbiamo anticipato la regola, come se valesse per tutti, ma senza dimostrarlo. Ora però siamo in grado di dimostrarlo.
- Dimostrare che
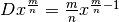 (il segno dell’esponente è qualsiasi).
(il segno dell’esponente è qualsiasi).
![Dx^\frac{m}{n}=D\sqrt[n]{x^m}=\frac{1}{n\sqrt[n]{\left(x^m\right)^{n-1}}}mx^{m-1}=\frac{mx^{m-1}}{n\sqrt[n]{x^{mn-m}}}=\frac{mx^{m-1}}{nx^\frac{mn-m}{n}}=\frac{m}{n}x^{m-1-\frac{mn-m}{n}}= \\ =\frac{m}{n}x^{\frac{mn-mn+m}{n}-1}=\frac{m}{n}x^{\frac{m}{n}-1}](../../../_images/math/c3a63aafc639d0251f231be5bd852f032f0ca9fe.png)
- Ricavare la regola della funzione inversa dalla regola della funzione composta.
Poiché la funzione composta è 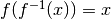 , allora la derivata risulta
, allora la derivata risulta
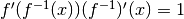 e quindi, se
e quindi, se 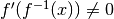 , ne
consegue che
, ne
consegue che 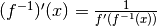 .
.
In questa sintetica dimstrazione abbiamo dato per scontato che la funzione inversa sia derivabile.
Riassunto¶
- Due nuove regole per la derivata. La derivata di una funzione composta è il prodotto delle derivate delle due funzioni che la compongono.
- La derivata dell’inversa di una funzione è il reciproco della derivata di quest’ultima.
- Abbiamo applicato le due regole, fra le altre cose, anche per dimostrare quanto anticipato nel Cap. 7 sulla derivata di una radice ennesima e sulla derivata di una potenza con esponente razionale qualsiasi.
).png)